Свойства разности натуральных чисел
Теорема 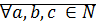
1) 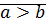 и
и 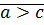 и
и 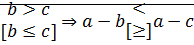
2) 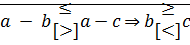
Доказательство:
1) 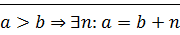
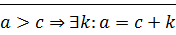
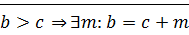
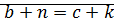
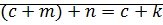
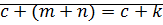
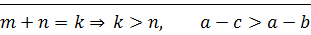
2) пусть 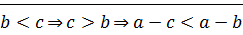 ?!
?! 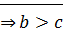 ⊠
⊠
Следствие Свойства справедливы для строгих и нестрогих неравенств.
Свойство
1) 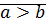 и
и 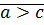 и
и 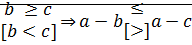
2) 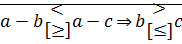
Частное натуральных чисел: определение и единственность. Свойства частного натуральных чисел
Определение: Частным чисел 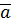 и
и 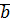 называется такое число
называется такое число 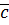 (если оно существует), что
(если оно существует), что 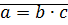 , обозначается
, обозначается  .
.
Теорема: Если частное 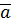 и
и 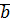 существует, то оно единственное
существует, то оно единственное
Доказательство:
Пусть 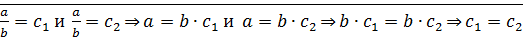 ⊠
⊠
Свойство 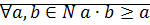
Доказательство 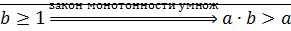 ⊠
⊠
Теорема
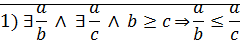
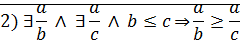
Доказательство:
1) 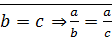
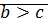
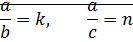
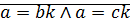
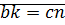
· 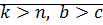 (дано)
(дано) 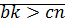 ?!
?!
· 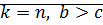 (дано)
(дано) 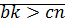 ?!
?!
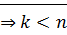 ⊠
⊠
24. Св-ва сложения и вычитания для натуральных чисел:
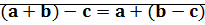
Теорема(свойства сложения и вычитания)
Если существуют соответствующие разности чисел 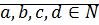 , то выполняются следующие равенства:
, то выполняются следующие равенства:
1) 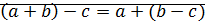
2) 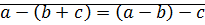
3) 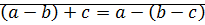
4) 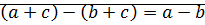
5) 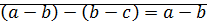
6) 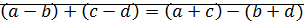
7) 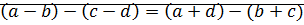
8) 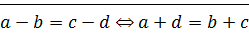
Доказательство:
1) 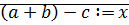
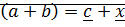
Проверим, подойдет ли вместо 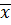 правая часть равенства.
правая часть равенства.
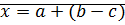 ?
?
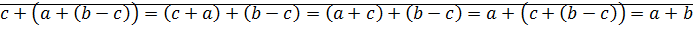
⊠
25. Св-ва сложения и вычитания для натуральных чисел: 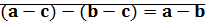
Теорема (свойства сложения и вычитания)
Если существуют соответствующие разности чисел 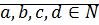 , то выполняются следующие равенства:
, то выполняются следующие равенства:
1) 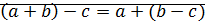
2) 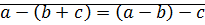
3) 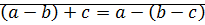
4) 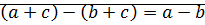
5) 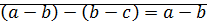
6) 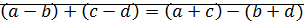
7) 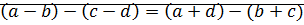
8) 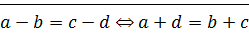
Доказательство:
5) 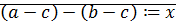 ,
,
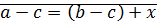
Проверим, подойдет ли вместо 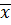 правая часть равенства.
правая часть равенства.
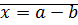 ?
?
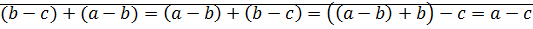 ⊠
⊠
26. Свойства сложения и вычитания для натуральных чисел:
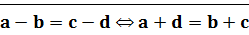
Теорема (свойства сложения и вычитания)
Если существуют соответствующие разности чисел 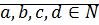 , то выполняются следующие равенства:
, то выполняются следующие равенства:
1) 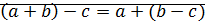
2) 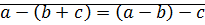
3) 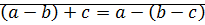
4) 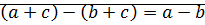
5) 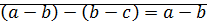
6) 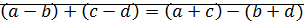
7) 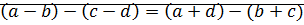
8) 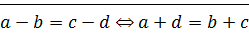
Доказательство:
8) 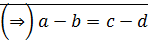
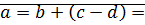 (1)
(1) 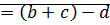
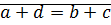
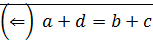
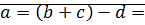 (1)
(1) 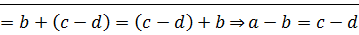 ⊠
⊠
27. Суммы и произведения нескольких натуральных чисел. Обобщенный закон дистрибутивности. n-кратное натурального числа. Степень натурального числа с натуральным показателем и ее свойства
Определение (индуктивное)Пусть 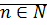 , тогда сумма натуральных чисел
, тогда сумма натуральных чисел 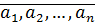
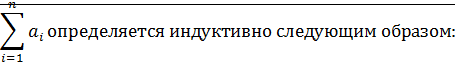
1) 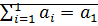
2) Если сумма определена для 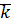 натуральных чисел и
натуральных чисел и 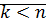 , то
, то
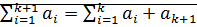 .
.
Замечание: Если все слагаемые в определении равны 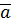 , то получим определение -кратного числу
, то получим определение -кратного числу 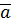 . Обозначается
. Обозначается 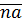 .
. 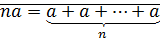 .
.
Определение (индуктивное) Пусть 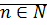 , тогда произведение натуральных чисел
, тогда произведение натуральных чисел
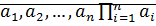 определяется индуктивно следующим образом:
определяется индуктивно следующим образом:
1) 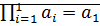
2) Если сумма определена для 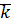 натуральных чисел и
натуральных чисел и 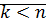 , то
, то
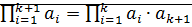 .
.
Теорема: 1) ( 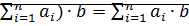 2) (
2) ( 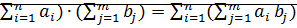
Доказательство: 1) ММИ по 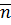
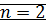
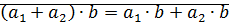
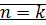 (
( 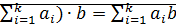 – верно
– верно
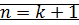
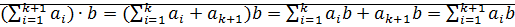 .
.
2) ММИ по 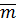
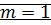 (
( 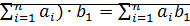
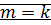 (
( 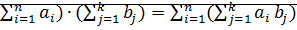 – верно
– верно
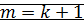 (
( 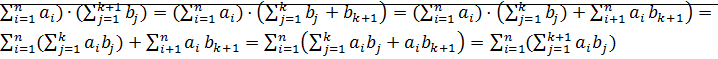 . ⊠
. ⊠
Свойство: 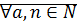
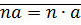 .
.
Доказательство:ММИ ( 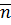 )
)
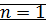
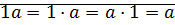
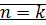
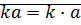 – верно
– верно
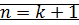
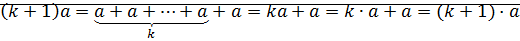 ⊠
⊠
Свойство: 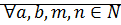
1) 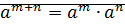 2)
2) 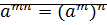
3) 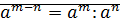 (если m>n) 4)
(если m>n) 4) 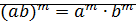
5) 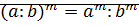 (если существует частное
(если существует частное 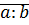 )
)
Доказательство: 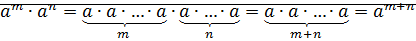 ⊠
⊠
Равномощные множества. Отношение эквивалентности «быть равномощными». Отрезок натурального ряда. Конечные и бесконечные множества
Определение: Множества 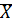 и
и 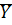 называются равномощными, если между ними существует взаимно-однозначное соответствие (биекция).
называются равномощными, если между ними существует взаимно-однозначное соответствие (биекция). 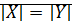 ;
; 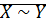
Свойство: Отношение «быть равномощным» является отношением эквивалентности
Доказательство:
· Рефлексивность: 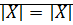
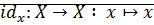
· Симметричность: 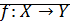 биекция
биекция 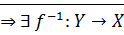 биекция
биекция
· Транзитивность: 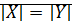 ,
, 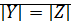 ;
;
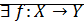 биекция,
биекция,
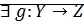 биекция
биекция
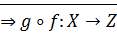 биекция ⊠
биекция ⊠
Определение: Пусть 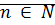 . Отрезком натурального ряда называется множество
. Отрезком натурального ряда называется множество 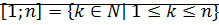
Пример: 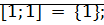
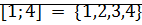
Определение: Множество 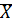 , равномощное отрезку
, равномощное отрезку 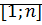 называется конечным.
называется конечным.
Число 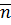 называется количеством элементов множества.
называется количеством элементов множества.
Множество, которое не является конечным, называется бесконечным.
