Типовые динамические звенья. Классификация
Основные типовые динамические звенья
Типовые динамические звенья. Классификация
Функциональные элементы, используемые в САУ, могут иметь самые различные конструктивное выполнение и принципы действия. Однако общность математических выражений, связывающих входные и выходные величины различных функциональных элементов, позволяет выделить ограниченное число так называемых типовых структурных звеньев. Каждому типовому алгоритмическому звену соответствует определенное математическое соотношение между входной и выходной величинами. Если это соотношение является элементарным (например, дифференцирование, умножение на постоянный коэффициент), то и звено называется элементарным.
Структурные звенья, которые описываются обыкновенными дифференциальными уравнениями первого и второго порядка, получили название типовых динамических звеньев.
Типовые динамические звенья являются основными составными частями структурных схем непрерывных САУ, поэтому знание их характеристик существенно облегчает анализ таких систем.
Классификацию типовых динамических звеньев удобно осуществить, рассматривая различные частные формы дифференциального уравнения
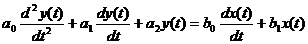 . (3.1)
. (3.1)
Значения коэффициентов уравнения (3.1) для наиболее часто применяемых звеньев приведены в табл. 3.1.
Таблица 3.1
Значения коэффициентов уравнения (3.1)
| № п/п | Наименование звена | a0 | a1 | a2 | b0 | b1 | Примечание |
| Безинерционное (пропорциональное) | k | ||||||
| Инерционное 1-го порядка (апериодическое) | T | k | |||||
| Инерционное 2-го порядка (апериодическое) |  | T1 | k | T1 ³ 2T2 | |||
| Инерционное 2-го порядка (колебательное) |  | T1 | k | T1 < 2T2 | |||
| Идеальное интегрирующее | k | ||||||
| Идеальное дифференцирующее | k | ||||||
| Реальное дифференцирующее | T | k |
Передаточные и переходные функции для наиболее часто применяемых звеньев приведены в табл. 3.2.
Таблица 3.2
Передаточные и переходные функции типовых динамических звеньев
| № | Наименование звена и описывающее его уравнение | Передаточная функция  | Переходная функция  |
Безинерционное (пропорциональное) 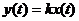 |  |   | |
Инерционное 1-го порядка (апериодическое) 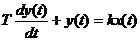 |  |   | |
Инерционное 2-го порядка (апериодическое) 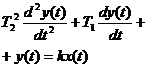 T1 ³ 2T2 T1 ³ 2T2 | 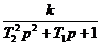 T1 ³ 2T2 T1 ³ 2T2 | 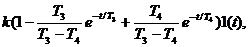 где где 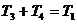 ; ;  . . 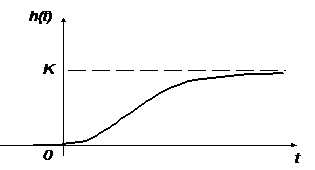 |
| № | Наименование звена и описывающее его уравнение | Передаточная функция  | Переходная функция  |
Инерционное 2-го порядка (колебательное) 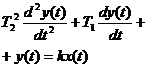 T1 < 2T2 T1 < 2T2 | 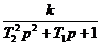 T1 < 2T2 T1 < 2T2 | 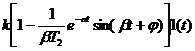 , где , где 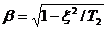  ; ;  ; ; 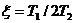 . .  | |
Идеальное интегрирующее 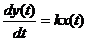 |  |   | |
Идеальное дифференцирующее  |  |  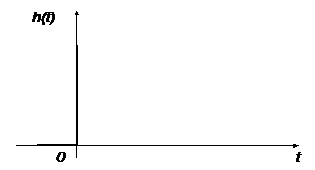 | |
Реальное дифференцирующее 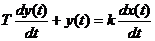 |  | 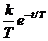    | |
Звено запаздывания 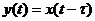 | 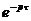 | 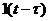  |
Основные типовые динамические звенья
Типовые динамические звенья. Классификация
Функциональные элементы, используемые в САУ, могут иметь самые различные конструктивное выполнение и принципы действия. Однако общность математических выражений, связывающих входные и выходные величины различных функциональных элементов, позволяет выделить ограниченное число так называемых типовых структурных звеньев. Каждому типовому алгоритмическому звену соответствует определенное математическое соотношение между входной и выходной величинами. Если это соотношение является элементарным (например, дифференцирование, умножение на постоянный коэффициент), то и звено называется элементарным.
Структурные звенья, которые описываются обыкновенными дифференциальными уравнениями первого и второго порядка, получили название типовых динамических звеньев.
Типовые динамические звенья являются основными составными частями структурных схем непрерывных САУ, поэтому знание их характеристик существенно облегчает анализ таких систем.
Классификацию типовых динамических звеньев удобно осуществить, рассматривая различные частные формы дифференциального уравнения
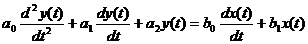 . (3.1)
. (3.1)
Значения коэффициентов уравнения (3.1) для наиболее часто применяемых звеньев приведены в табл. 3.1.
Таблица 3.1
Значения коэффициентов уравнения (3.1)
| № п/п | Наименование звена | a0 | a1 | a2 | b0 | b1 | Примечание |
| Безинерционное (пропорциональное) | k | ||||||
| Инерционное 1-го порядка (апериодическое) | T | k | |||||
| Инерционное 2-го порядка (апериодическое) |  | T1 | k | T1 ³ 2T2 | |||
| Инерционное 2-го порядка (колебательное) |  | T1 | k | T1 < 2T2 | |||
| Идеальное интегрирующее | k | ||||||
| Идеальное дифференцирующее | k | ||||||
| Реальное дифференцирующее | T | k |
Передаточные и переходные функции для наиболее часто применяемых звеньев приведены в табл. 3.2.
Таблица 3.2
Передаточные и переходные функции типовых динамических звеньев
| № | Наименование звена и описывающее его уравнение | Передаточная функция  | Переходная функция  |
Безинерционное (пропорциональное) 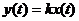 |  |   | |
Инерционное 1-го порядка (апериодическое) 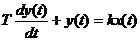 |  |   | |
Инерционное 2-го порядка (апериодическое) 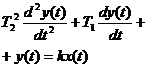 T1 ³ 2T2 T1 ³ 2T2 | 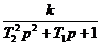 T1 ³ 2T2 T1 ³ 2T2 | 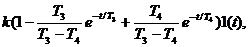 где где 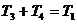 ; ;  . .  |
| № | Наименование звена и описывающее его уравнение | Передаточная функция  | Переходная функция  |
Инерционное 2-го порядка (колебательное) 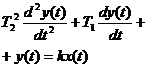 T1 < 2T2 T1 < 2T2 | 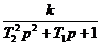 T1 < 2T2 T1 < 2T2 | 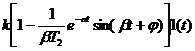 , где , где 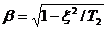  ; ;  ; ; 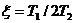 . .  | |
Идеальное интегрирующее 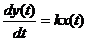 |  |   | |
Идеальное дифференцирующее  |  |   | |
Реальное дифференцирующее 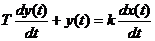 |  | 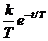    | |
Звено запаздывания 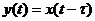 | 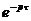 | 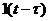  |
