Предмет и основные подходы ТПР

Предмет и основные подходы ТПР

Подходы:

1) Дескриптивный

2) Нормативный

3) Прескриптивный

Этапы процесса ПР

1)Предварительный анализ проблем:

1) Определение цели

2) Уровень рассмотрения задачи

3) Элементы и структура

4) Используемые ресурсы и критерии качества функционирования

5) Основные ограничения и противоречия

2) Постановка задачи принятия решения

1) Формулирование задачи

2) Определение типа задачи

3) Определение множества вариантов

4) Определение критериев выбора

5) Определение метода решения задачи

3) Получение исходных данных

1) Определение способа измерения вариантов

2) В качестве источников информации могут выступать:

- статистические данные

- результаты имитационного или матем. моделирования

- результаты экспертного оценивания

4) Решение задачи с использованием выбранных методов, ВТ, экспертов

5) Анализ и интерпретация полученных результатов.

Классификация ЗПР

<W,A,K,X,F,G,D,T>

W – постановка задачи с точностью до модели решения

A – множество допустимых вариантов или альтернатив (может быть закрытым или открытым)

К – множество критериев выбора

Х – множество методов измерения предпочтения

F – отображение множества допустимых альтернатив на множестве критериев

G – система предпочтения эксперта

Т – резерв времени на принятие решений

Традиционные классификации:

1) По виду отображения:

Отображения: детерминированное, вероятностное, нечеткое

в условиях определенности ,в условиях риска, в условиях неопределенности.

2) По мощности множества К:

К может содержать 1 элемент или несколько, соответственно задачи однокритериевые и многокритериевые.

3) По типу системы G

задачи индивидуального и коллективного принятия решений.

В рамках этих классификаций выделяют:

1) ЗПР в условиях определенности

2) ЗПР в условиях риска

Принцип Парето

Принцип единогласия

Оптимальным по Парето решением является такое решение X, что для решения Z, если кто-либо (хотя бы один участник коллектива) считает, что Z лучше X, то обязательно найдется кто-то другой, считающий, что X лучше Z. Принцип Парето означает, что поиск решения надо вести до тех пор, пока все единогласно не скажут, что X – оптимально. Для любого другого решения Z будет хотя бы один голос против.

Равновесие по Нэшу. Принцип ограниченной рациональности.

Равновесие по Нэшу:

Существует ситуация, когда принятие решений индивидуально отдельным участником коллектива неэффективно для всех участников.

Принцип огр. рациональности:

В соответствии с данным принципом существуют объективные пределы. способности человека описывать и правильно передавать информацию о сложных ситуациях , осмысливать эту ситуацию, одинаково рассматривать несколько вариантов решений и выбирать из каких-либо рациональных соображений один вариант.

Принцип минимакса. Геометрическая интерпретация.

Принцип гарантированного результата.

Известно, что если 1 сторона выберет действие Ai, некоторая сторона - Bj, то этой паре однозначно соответствует выигрыш Uij.

Если Uij>0 то это выигрыш А, если Uij<0 то B.

Все решения можно представить в виде матрицы.

Предположим, что каждая из сторон стремится получить гарантированный результат.

Предположим, что А выиграет, а В проиграет, тогда

для А – гарантированный выигрыш

для В – гарантированный проигрыш

Рассмотрим для стороны А отдельно i вариант действий:

Ai |Ui1|Ui2|…|Uim|

min(Uij)=Uiг – гарант. для А

если выполняем гарантированный выигрыш для каждой строки, то получаем:

|U1г|

|U2г|

|… |

|Unг|

max(Uiг) = maxmin (Uij)

гарантированный выигрыш для стороны А дает минимаксное решение

min(Uij) = Uiг

Bj

|U1j|

|U2j|

|… |

|Unj|

Ujг = max (Uij)

Uiг|Uiг|…|Umг | -> min(Uiг) = minmax(Uij) = Uгг

Uгг = U*гг

если эти величины совпадают и соответствуют одному и тому же элементу платежной матрицы, то считается что в системе есть седловая точка.

граф. отображение: фигура типа «седло»

Постановка задачи ЛП.

Для постановки задачи ЛП необходимо сформировать следующие 3 элемента:

1) Переменные, которые следует определить

2) Целевая функция. подлежащая оптимизации

3) Ограничения, которым должна удовлетворять переменная

Алгоритм cимплекс-метода.

Основная идея:

Начиная с некоторого допустимого базисного решения пытаются найти другое базисное решение, которое улучшает значение целевой функции.

Алгоритм можно записать в 3 формах:

1) В виде системы уравнений

2) В табличной форме

3) В матричной форме

Условие оптимальности:

Вводимой переменной в задаче макс-ии является небазисная переменная, имеющая наибольший отрицательный коэффициент в Z строке.

Условие допустимости:

Выбирается переменная, для которой отношение значения правой части ограничения к положительному коэффициенту ведущего столбца минимально.

Особые случаи задачи ЛП.

1) Вырожденность (одна или несколько переменных могут принять нулевое значение)

Причина: наличие одного избыточного ограничения

2) Альтернативное оптимальное решение

Выр-е ЦФ с точностью до константы совпадает с выр-м одного из ограничений.

3) неограниченное решение (неограниченность ОДР хотя бы по 1 направлению)

4) Отсутствие допустимых решений

В случаях 3 и 4 постановка задачи некорректна или плохая формализация.

Основные понятия сетевых моделей.

Рассматриваются следующие виды задач:

1) построение сети газопроводов с минимальной стоимостью

2) проложение кратчайшего маршрута между двумя узлами по существующей сети, по существующей метрике.

3) определение макс. пропускной способности сети трубопроводов заданной конфигурации.

4) определение потока максимальной пропускной способности и наименьшей стоимости.

5) составление временного графика выполнения работ.

Дерево – граф, в котором отсутствует цикл.

Алгоритм Дейкстры. Пример

Разработан для нахождения кратчайшего пути между заданными исходным узлом и любым узлом сети.

строится набор таблиц типа:

Узел	Метки	Статус
	[0,-]	П
	[100,1]	В
	[30,1]	В->П

Алгоритм Флойда. Пример

Является более общим, поскольку позволяет найти кратчайшее расстояние между любыми 2-мя узлами сети.

В этом алгоритме сеть представлена 2-мя матрицами:

1) матрица расстояний

2) матрица последовательности номеров узлов.

Основная идея:

Для любых 3 узлов проводится соотношение:

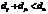Если это соотношение выполняется, производится замена на составляющую.

Метод Форда-Фалкерсона.

Перебор сквозных путей от истока к стоку с вычислением пропускных способностей этих путей.

Для работы алгоритма требуется чтобы в структуре сети были только 1 исток и 1 сток.

Для приведения к требуемому виду добавляем фиктивный сток.

(Сij, Cji) – текущая или остаточная пропускная способность.

Шаг 1: Для всех ребер пложим остаточную пропускную способность равной первоначальной пропускной способности.

Шаг2: Определяем множество Si, как множество узлов j, в который можно будет перейти из узла i по ребру с положительной остаточной пропускной способностью, т.е. Cij>0 .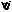

Если Si ≠ Ø, то выполняем ш3, иначе переходим к ш4.

Шаг 3: на Si выбираем k:

Cik=max{Cij}

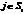
Если k=n, то сквозной путь найден, переходим к ш5, иначе присваиваем i=k и переходим к ш2.

Шаг 4: (откат назад)

Если i=1, то сквозной путь невозможен, то находим узел с номером r, непосредственно из списка доступных узлов узла R.

Шаг 5: (Определение остаточной сети)

Np={1,k1,k2,…,n}

исток сток

Np – множество узлов, входящих в p-й сквозной путь от истока к стоку n.

Тогда максимальный поток, проходящий по этому пути определяется:

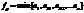
Остаточные пропускные способности ребер, составляющих сквозной путь уменьшаются на величину fp в направлении движения потока и увеличения на эту же величину в обратном направлении.

Шаг 6: Решение

При m найденных сквозных путях макс поток определяется следующим образом:

Оптимальный поток через ребро (i,j) определяется:

а) m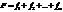

б)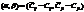

Задача о загрузке. Пример

Задача о рациональной загрузке т/с с ограничением по вместимости или грузоподъемности

Для каждой единицы груза каждого вида указывается масса или объем, а также указывается приносимая прибыль или полученный эффект.

Задача состоит в определении загрузки т/с таким набором грузов, которые приносят наибольшую прибыль или наибольший эффект.

Этапы:

1) В качестве i этапа возьмем загрузку i-го рассмотрения

2) Варианты решения: количество единиц i-го груза

В качестве состояния Xi возьмем суммарный вес грузов, решения о погрузке которых приняты на этапах с i до n для метода обратной прогонки.

fi(Xi) – максимальная суммарная прибыль от этапов i, i+1,..n при заданном состоянии Xi на i этапе.

fi(Xi) = max {rimi + fi+1(Xi+1)}= max{rimi + fi+1(xi-Wmi)}

Wi – масса i-го вида груза

W – общая грузоподъемность т/с.

Пример – задача о загрузке самолета.

35.Задача планирования рабочей силы. Пример

При выполнение некоторых проектов число рабочих, необходимые для выполнения какого-либо проекта, регулируется путем их найма и увольнения. Так как наем и увольнение рабочих связано с дополнительными затратами нужно определить как должна регулир. Численность рабочих для реализации проекта. Этапы:

Этап i- порядковый номер недели.

Вариантами решений на этапе-x_i-1-кол-во раб-щих на i-ой неделе.

Функция управления на этапе- u(x_i)=C₁(x_i-b_i)+C₂(x_i –x_i-1).

Реккурентное уравнение-f_i(x_i-1)=min{ C₁(x_i-b_i)+C₂(x_i –x_i-1)+f_i+1(x₁)},i=1,2…n. Вычисления начинаются с этапа n при x_n=b_n.

Задача замены оборудования. Пример

старое оборудование изнашивается и расходы на эксплуатацию могут превысить расходы на покупку нового.

Задача замены оборудования сводится к определению оптимального срока эксплуатации механизма. Этапы:

Этап I представляется номером года.

Вариантами решения на i-ом этапе является продолжительность эксплуатации или замена механизма в начале года.

Состоянием на i-ом этапе является срок экспл. T

Функция управления-u(t)=r(t)-c(t)

Реккурентное уравнение-

f_i(t)-max

Пример – задача про газонокосилку.

Цепи и процессы Маркова. Основные понятия.

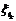- случайная величина, характеризующая состояние системы в момент tk.

Состояния в момент tk. В которых может находиться система формируют полную группу событий

Число состояний системы может быть конечным или бесконечным.

Среди всех случайных процессов представляют Марковские процессы и Марковские цепи.

Цепь Маркова является частным случаем Марковских процессов. При изучении краткосрочного и долгосрочного поведения стохастических систем с дискретным множеством состояний.

Марковский процесс описывает поведение стохастической системы, в которой наступление очередного состояния зависит только от непосредственно предшествующего состояния системы.

Семейство случайных величин будет процессом Маркова тогда и только тогда, когда оно обладает Марковским свойством, при условии:

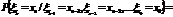
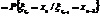
для всех возможных значений случайных величин.

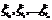- одноименные переходные вероятности

Предмет и основные подходы ТПР

Подходы:

1) Дескриптивный

2) Нормативный

3) Прескриптивный

Этапы процесса ПР

1)Предварительный анализ проблем:

1) Определение цели

2) Уровень рассмотрения задачи

3) Элементы и структура

4) Используемые ресурсы и критерии качества функционирования

5) Основные ограничения и противоречия

2) Постановка задачи принятия решения

1) Формулирование задачи

2) Определение типа задачи

3) Определение множества вариантов

4) Определение критериев выбора

5) Определение метода решения задачи

3) Получение исходных данных

1) Определение способа измерения вариантов

2) В качестве источников информации могут выступать:

- статистические данные

- результаты имитационного или матем. моделирования

- результаты экспертного оценивания

4) Решение задачи с использованием выбранных методов, ВТ, экспертов

5) Анализ и интерпретация полученных результатов.

Классификация ЗПР

<W,A,K,X,F,G,D,T>

W – постановка задачи с точностью до модели решения

A – множество допустимых вариантов или альтернатив (может быть закрытым или открытым)

К – множество критериев выбора

Х – множество методов измерения предпочтения

F – отображение множества допустимых альтернатив на множестве критериев

G – система предпочтения эксперта

Т – резерв времени на принятие решений

Традиционные классификации:

1) По виду отображения:

Отображения: детерминированное, вероятностное, нечеткое

в условиях определенности ,в условиях риска, в условиях неопределенности.

2) По мощности множества К:

К может содержать 1 элемент или несколько, соответственно задачи однокритериевые и многокритериевые.

3) По типу системы G

задачи индивидуального и коллективного принятия решений.

В рамках этих классификаций выделяют:

1) ЗПР в условиях определенности

2) ЗПР в условиях риска

Принцип Парето

Принцип единогласия

Оптимальным по Парето решением является такое решение X, что для решения Z, если кто-либо (хотя бы один участник коллектива) считает, что Z лучше X, то обязательно найдется кто-то другой, считающий, что X лучше Z. Принцип Парето означает, что поиск решения надо вести до тех пор, пока все единогласно не скажут, что X – оптимально. Для любого другого решения Z будет хотя бы один голос против.