Линейные ДУ с постоянными коэффициентами
Уравнение вида
 |
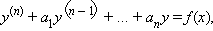где a1, …, an – некоторые постоянные, называется линейным дифференциальным уравнением с постоянными коэффициентами.
Всякое решение однородного уравнения первого порядка
 |
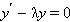имеет вид
 |
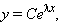где C – постоянная.
Уравнение вида
 |
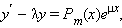где Pm (x) – многочлен степени m, μ – постоянная, имеет частное решение вида
 |
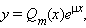если μ ≠ λ, и вида
 |
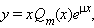если μ = λ. Здесь Qm (x) – многочлен степени m.
В общем случае у однородного линейного дифференциального уравнения с постоянными коэффициентами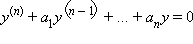 
имеется так называемое характеристическое уравнение 
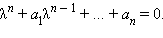Корни этого уравнения – характеристические числа – являются показателями степеней слагаемых, входящих в решение. Если среди корней уравнения 
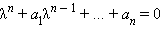нет кратных, то решением однородного уравнения является функция вида 
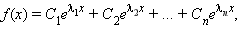где все 
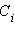– некоторые константы, зависящие от начальных условий. Количество слагаемых в этой функции совпадает со степенью дифференциального уравнения. Если же, скажем, 
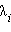– корень характеристического уравнения кратности m, то соответствующее слагаемое принимает вид 
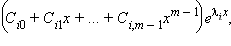а общее количество слагаемых, входящих в решение однородного дифференциального уравнения уменьшается на m – 1.
Метод вариации произвольных постоянных
Этот метод основан на том, что форма записи решения неоднородного уравнения такая же, что и у соответствующего однородного, с той лишь разницей, что произвольную постоянную С следует считать некоторой функцией переменной t, С = С(t), то есть x(t)=C(t)e (3.5)
Функция C(t) должна быть такой, чтобы при подстановке (3.5) в уравнение (3.1) последнее обращалось в тождество. Подставляя x(t) и C'(t)e =f(t) или C'{t)=f(t)e
Интегрируя, находим выражение для C(t): (3.6)
Подставляя полученное выражение в (3.4), получаем общее решение линейного неоднородного уравнения (3.1) в виде . (3.7)
Заметим, что первое слагаемое в формуле (3.7) является частным решением линейного неоднородного уравнения (3.1), в чем можно убедиться непосредственной проверкой. Второе слагаемое является общим решением соответствующего однородного уравнения (3.3). Этот результат подтверждает известное свойство решений неоднородного уравнения.
Приведенные рассуждения позволяют сформулировать алгоритм решения уравнения (3.1).
Системы обыкновенных дифференциальных уравнений
Рассмотрим систему обыкновенных дифференциальных уравнений n–го порядка
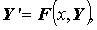или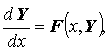 
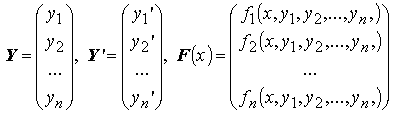
Задачей Коши для для этой системы называется следующая задача: найти такое решение Y = Y(x) системы Y' = F(x,Y), что Y(x0)=Y0, гдеY0 — некоторый постоянный вектор.
Вектор-функция Y = Y(x,С), зависящая от произвольного вектора С, называется общим решением системы, если:
— при любом векторе C, вектор-функция Y(x,С) является решением системы;
— какова бы ни была начальная точка ((x0, Y0), существует такой вектор С(0), что Y(x(0),С(0)) = Y0.