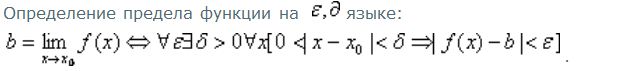Теоремы о величинах, обратных бесконечно большим и бесконечно малым

Теорема 1. Если функция f(x) является бесконечно большой при x→a, то функция 1/f(x) является бесконечно малой при x→a.

Теорема 2. Если функция f(x) - бесконечно малая при x→a (или x→∞) и не обращается в нуль, то y=1/f(x) является бесконечно большой функцией.

Предел последовательности

Предел последовательности – это число, к которому члены последовательности стремятся при неограниченном возрастании номера n.

а_n А при n N

16. Определение предела последовательности на языке «ε» - «N»

Число А – предел последовательности {а_n}, если для любого, сколь угодно малого числа ε> 0 найдется такое число N (зависящее от ε),что для всех членов последовательности с номерами n>N будет выполнено неравенство:

Iа_n - АI<ε

Свойства последовательностей, имеющих предел

Имеют место следующие арифметические свойства пределов вещественных последовательностей:

1. 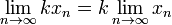, где 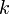— константа;

2. 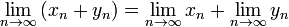, если указанные пределы существуют;

3. 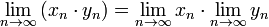при том же условии;

4. 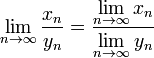, если пределы существуют и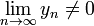

Геометрический смысл предела последовательности

Число а – предел последовательности {а_n}, если для любой е-окрестности точки а, найдется натуральное число N, что все значения а_n, для которых n>N, падут в е-окрестности точки а.

Теорема о единственности предела последовательности

Теорема. Последовательность не может иметь больше одного

предела.

Доказательство. Следует из того, что последовательность не

может одновременно приближаться к двум разным числам

одновременно.

Выберем ε значительно меньше разницы между числами A и B.

Тогда очевидно, что мы не сможем указать такого номера N,

начиная с которого одновременно будут выполнены два

условия:

Iа_{n -} АI <ε иIа_{n -}ВI <ε

Теорема о связи последовательности, имеющей предел, ее предела и бесконечно малой

Для того, чтобы последовательность а_nсходилась, необходимо и достаточно, чтобы ее можно было представить в виде суммы какого-то числа А и бесконечно малой последовательности.

{а_n} = А + {α_n}

{а_{n -} А}= {α_n}

Теоремы об арифметических свойствах пределов последовательностей.

Имеют место следующие арифметические свойства пределов вещественных последовательностей:

Признаки существования предела последовательности

1Теорема (признак существования предела). Теорема Вейерштрасса Если последовательность {an} монотонна и ограничена, то она имеет предел.

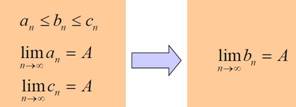
2Теорема (признак существования предела).или теорема о двух милиционерах. Если одна

последовательность заключена между двумя другими, имеющими одинаковый предел, то она имеет тот же предел.

3Критерий Коши:Для существования предела последовательности {Xn}, необходимо и достаточно, чтобы для любого эпсилон>0 существовало N=N(эпсилон) такое, что для всех n>N и p>0, |Xn-X(n+p)|<эпсилон.

Замечательный предел типа e

Математики рассматривали последовательность(а эн равное лимит стремящийся к бесконечности (1-1+/n) в степени n) Эта последовательность {an } возрастает и ограничена сверху (доказательство это-

го любознательные студенты могут посмотреть в учебниках математики). Следовательно, существует предел этой последовательности.Его и обозначили через е в честь математика Эйлера (1707-1783).

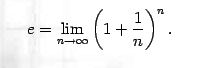
Предел функции в точке.

Имеется также определение предела функции, при стремлении

аргумента к определенному значению а, называемого пределом функции в

точке. Число A называется пределом функции y = f(x) при x → a, если для любого, даже сколь угодно малого положительного для любого, даже сколь угодно малого ε > 0, найдется такое число δ > 0 (зависящее от ε), что для всех x из δ-окрестности точки a, выполнено неравенство: 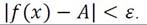Это определение называется определением на языке ε и δ,предложено французским математиком Огюстеном Коши и используется с начала XIX века по настоящее время, поскольку обладает необходимой математической строгостью и точностью.

Запишем на языке кванторов определение предела функции в точке:

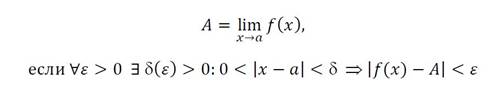
25. определение предела функции на языке