Семинар. Функциональные последовательности и ряды. Равномерная сходимость.
Семинар. Функциональные последовательности и ряды. Равномерная сходимость.
Определение: Если каждому натуральному 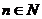 поставлена в соответствие функция
поставлена в соответствие функция 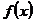 , определенная на множестве Х, то говорят, что задана функциональная последовательность
, определенная на множестве Х, то говорят, что задана функциональная последовательность 
Определение: Если числовая последовательность 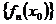 сходится (расходится), то говорят, что исходная функциональная последовательность
сходится (расходится), то говорят, что исходная функциональная последовательность  сходится (расходится) в точке
сходится (расходится) в точке 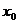 .
.
Определение: Говорят, что функциональная последовательность  сходится на множестве
сходится на множестве  к функции
к функции  , если она сходится в каждой точке
, если она сходится в каждой точке  :
:
 .
.
· Найти предельную функцию  . (Отв. 0, если
. (Отв. 0, если 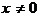 )
)
· Найти предельную функцию  (Ответ: x)
(Ответ: x)
· Найти предельную функцию 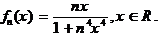 (Ответ: 0)
(Ответ: 0)
Если задана точка 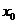 , то в этой точке исследование сходимости функциональной последовательности сводится к исследованию сходимости числовой последовательности. Однако существует понятие сходимости, учитывающее поведение функций
, то в этой точке исследование сходимости функциональной последовательности сводится к исследованию сходимости числовой последовательности. Однако существует понятие сходимости, учитывающее поведение функций 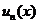 на некотором множестве точек
на некотором множестве точек 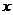 .
.
Определение: Говорят, что функциональная последовательность  сходится равномерно на множестве Х, если:
сходится равномерно на множестве Х, если: 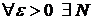 (один и тот же для всех
(один и тот же для всех 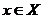 ) такой, что
) такой, что 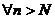 и
и 
 .
.
Обозначим такую сходимость  на Х.
на Х.
Теорема (Критерий Коши равномерной сходимости функциональной последовательности):
Для того чтобы функциональная последовательность  сходилась равномерно на множестве Х к некоторой функции
сходилась равномерно на множестве Х к некоторой функции 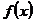 , необходимо и достаточно, чтобы
, необходимо и достаточно, чтобы  – натурального,выполнялось следующее условие:
– натурального,выполнялось следующее условие: 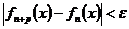 сразу для
сразу для 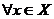 .
.
Графическая иллюстрация равномерной сходимости.

Неравенство  означает, что при
означает, что при  график любой функции
график любой функции 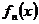 будет лежать в e-окрестности графика функции и
будет лежать в e-окрестности графика функции и 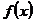 .
.
Сформулируем «практический» критерий равномерной сходимости функциональной последовательности, вытекающий из определения равномерной сходимости функциональной последовательности.
Функциональная последовательность  сходится равномерно на множестве Х, если
сходится равномерно на множестве Х, если 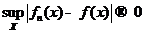 при
при 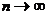 , т.е.
, т.е. 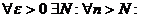
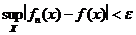 .
.
При исследовании функциональной последовательности на равномерную сходимость
- находим
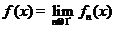 ;
; - находим
 ;
; - определяем, равен или не равен нулю
 .
.
Если 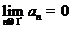 , то последовательность сходится равномерно, в противном случае она сходится неравномерно.
, то последовательность сходится равномерно, в противном случае она сходится неравномерно.
· Пример:  ,
,  Д2746 (б) − сходится в каждой точке, но не равномерно.
Д2746 (б) − сходится в каждой точке, но не равномерно.
· Исследовать на равномерную сх-ть: 1). 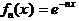 , а)
, а)  ;(неравномерно) б)
;(неравномерно) б)  (равномерно).
(равномерно).
Для отыскания точной верхней грани удобно найти точку максимума из условия равенства нулю производной:
·  (равномерно)
(равномерно)
· 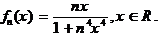 (неравномерно)
(неравномерно)
· При каких  последовательность
последовательность  сходится равномерно на R? (Отв.
сходится равномерно на R? (Отв.  <1)
<1)
Функциональные ряды.
Членами функциональных рядов  являются функции
являются функции 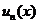 , определенные на множестве Х.
, определенные на множестве Х.
Определение: Если числовой ряд  сходится (расходится), то говорят, что функциональный ряд
сходится (расходится), то говорят, что функциональный ряд  сходится (расходится) в точке
сходится (расходится) в точке 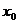 .
.
Определение: Если функциональный ряд  сходится в каждой точке
сходится в каждой точке  , то говорят, что указанный ряд сходится на множестве
, то говорят, что указанный ряд сходится на множестве  .
.
Найдите область сходимости функционального ряда.
·  (Д2716)
(Д2716)
· 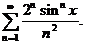 (Д2721) (Ответ:
(Д2721) (Ответ: 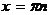 )
)
·  (Д2723) (Ответ: сходится абсолютно при
(Д2723) (Ответ: сходится абсолютно при  , сходится условно при
, сходится условно при  .)
.)
Определение: Говорят, что функциональный ряд 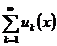 сходится равномерно к функции
сходится равномерно к функции 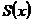 на множестве Х, если последовательность его частичных сумм сходится равномерно к функции
на множестве Х, если последовательность его частичных сумм сходится равномерно к функции  при
при 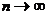 на множестве Х, то есть
на множестве Х, то есть 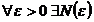 такой, что
такой, что  выполняется условие
выполняется условие  сразу для
сразу для 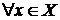 .
.
· Исследуйте на равномерную сходимость функциональный ряд 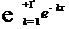 ,
, 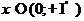 .
.
Теорема 2 (Критерий Коши равномерной сходимости функционального ряда):
Для того, чтобы функциональный ряд равномерно сходился к своей сумме необходимо и достаточно, чтобы  – натурального,выполнялось
– натурального,выполнялось 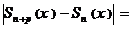
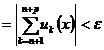 сразу для
сразу для 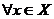 .
.
· Исследуйте на равномерную сходимость функциональный ряд 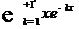 ,
, 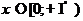 .
.
Сходимость в среднем.
Определение.Говорят, что последовательность 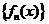 сходится в среднем к функции
сходится в среднем к функции 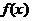 на сегменте
на сегменте 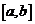 , если
, если  .
.
Докажите, что функциональная последовательность  сходится в среднем на множестве
сходится в среднем на множестве  .
.
Докажите, что функциональная последовательность  не сходится в среднем на множестве
не сходится в среднем на множестве  .
.
На дом: Д2746, 2747, 2748, 2752,2755,2756(а)(посл-ти); Д2767, 2768, 2769;
Д2774(б,в,г,к,л)(Вейерштрасс), Д2778, 2780(Д.-А.).
Докажите, что функциональная последовательность 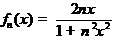 сходится в среднем на множестве
сходится в среднем на множестве  .
.
Докажите, что функциональная последовательность 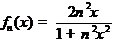 не сходится в среднем на множестве
не сходится в среднем на множестве  .
.
Выучить пять основных разложений ( формула Маклорена)!!
Тема следующего семинара: «Функциональные последовательности и ряды. Равномерная сходимость». Подготовиться к семинару можно, прочтя Ильин-Позняк часть II гл.I §1 п. 6 §2п.1,2.
На следующем семинаре в качестве контроля – контрольная по домашнему заданию - 3 варианта – задачи Д2637 (сравнение), Д2580 (Даламбер), Д2683 (Лейбниц).
Степенные ряды.
Напомнить определение степенного ряда, формулу Коши-Адамара, определение сходимости и равномерной сходимости, формулы пяти основных разложений в ряд Тейлора.
· Определить радиус и интервал сходимости и исследовать поведение в граничных точках интервала сходимости следующих рядов:
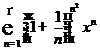 (Д 2816),
(Д 2816),
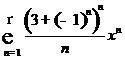 (Д 2828).
(Д 2828).
· Разложить функцию 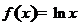 в степенной ряд по степеням разности
в степенной ряд по степеням разности 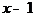 и определить интервал сходимости разложения (Д 2840).
и определить интервал сходимости разложения (Д 2840).
· Разложить функцию  в степенной ряд а) по степеням x, б) по степеням разности
в степенной ряд а) по степеням x, б) по степеням разности 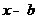 , где
, где 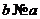 в) по степеням
в) по степеням  и определить интервал сходимости разложения (Д 2839).
и определить интервал сходимости разложения (Д 2839).
· Применяя почленное дифференцирование, вычислите сумму ряда 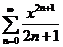 (Д 2906),
(Д 2906),
· Применяя почленное интегрирование, вычислите сумму ряда 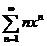 ( Д 2911).
( Д 2911).
На дом: ВОС гл.I № 724: Для функциональной последовательности 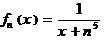 ,
, 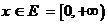 установить сходимость, исследовать её на равномерную сходимость и выяснить, справедливо или нет равенство
установить сходимость, исследовать её на равномерную сходимость и выяснить, справедливо или нет равенство 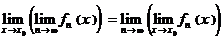 при
при 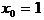 .
.
Д2794. Этот пример показывает, что признак возможности предельного перехода достаточный, но не необходимый.
Д 2808.1
Определить область существования функции 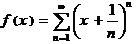 и исследовать её на непрерывность.
и исследовать её на непрерывность.
Д 2804 (этот пример показывает, что признак интегрирования последовательности, лишь достаточный, но не необходимый.)
ВОС гл.I № 744: Для функциональной последовательности 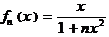 ,
, 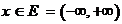 а) выяснить вопрос о равномерной сходимости последовательности б) выяснить вопрос о равномерной сходимости последовательности из производных, в) справедливо или нет равенство
а) выяснить вопрос о равномерной сходимости последовательности б) выяснить вопрос о равномерной сходимости последовательности из производных, в) справедливо или нет равенство 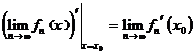 ?
?
Д 2826, 2829, 2858, 2851, 2852, 2853, 2873, 2907, 2912.
На следующем семинаре в качестве контроля - контрольная по домашнему заданию - 3 варианта – задачи 2851, 2852, 2853 (разложение в ряд Маклорена).
Семинар. Функциональные последовательности и ряды. Равномерная сходимость.
Определение: Если каждому натуральному 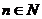 поставлена в соответствие функция
поставлена в соответствие функция 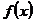 , определенная на множестве Х, то говорят, что задана функциональная последовательность
, определенная на множестве Х, то говорят, что задана функциональная последовательность 
Определение: Если числовая последовательность 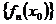 сходится (расходится), то говорят, что исходная функциональная последовательность
сходится (расходится), то говорят, что исходная функциональная последовательность  сходится (расходится) в точке
сходится (расходится) в точке 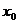 .
.
Определение: Говорят, что функциональная последовательность  сходится на множестве
сходится на множестве  к функции
к функции  , если она сходится в каждой точке
, если она сходится в каждой точке  :
:
 .
.
· Найти предельную функцию  . (Отв. 0, если
. (Отв. 0, если 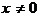 )
)
· Найти предельную функцию  (Ответ: x)
(Ответ: x)
· Найти предельную функцию 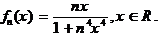 (Ответ: 0)
(Ответ: 0)
Если задана точка 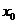 , то в этой точке исследование сходимости функциональной последовательности сводится к исследованию сходимости числовой последовательности. Однако существует понятие сходимости, учитывающее поведение функций
, то в этой точке исследование сходимости функциональной последовательности сводится к исследованию сходимости числовой последовательности. Однако существует понятие сходимости, учитывающее поведение функций 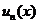 на некотором множестве точек
на некотором множестве точек 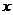 .
.
Определение: Говорят, что функциональная последовательность  сходится равномерно на множестве Х, если:
сходится равномерно на множестве Х, если: 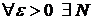 (один и тот же для всех
(один и тот же для всех 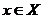 ) такой, что
) такой, что 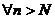 и
и 
 .
.
Обозначим такую сходимость  на Х.
на Х.
Теорема (Критерий Коши равномерной сходимости функциональной последовательности):
Для того чтобы функциональная последовательность  сходилась равномерно на множестве Х к некоторой функции
сходилась равномерно на множестве Х к некоторой функции 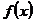 , необходимо и достаточно, чтобы
, необходимо и достаточно, чтобы  – натурального,выполнялось следующее условие:
– натурального,выполнялось следующее условие: 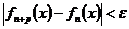 сразу для
сразу для 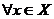 .
.
