Метод разделения переменных.
Метод разделения переменных носит также название метода Фурье и является наиболее распространенным методом решения уравнений с частными производными. Рассмотрим его на примере струны с закрепленными концами. Уравнение колебаний
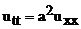 (70)
(70)
Граничные условия
 ,
,  (71)
(71)
Начальные условия
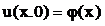 ,
,  (72)
(72)
Будем искать решение в виде произведения функции зависящей только от x и только от t:
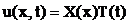 (73)
(73)
Подставляя (73) в (70) получаем
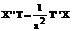
Разделив левую и правую часть нашего равенства на произведение XT:
 (74)
(74)
В (74) левая часть является функцией только x, правая часть – только t, причем оно должно выполняться во всей области значений переменных. Это возможно только в том случае если правая и левая часть равны некой константе:
 (75)
(75)
В результате получаем ОДУ для нахождения неизвестных функций X и T:
 (76)
(76)
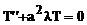 (77)
(77)
Из граничных условий
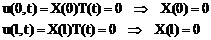
Таким образом для нахождения функции X(x) мы получили задачу на собственные функции и собственные значения (задачу Штурма-Лиувилля):
Найти значения параметра λ (собственные значения), при которых существуют нетривиальные решения задачи
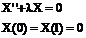 (78)
(78)
А также соответствующие им решения – собственные функции.
Рассмотрим возможные значения параметра λ.
1. λ<0
в этом случае общее решение уравнения (78) ищем в виде:
 Тогда:
Тогда: 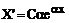

Подставляем в (78):
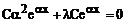 Отсюда
Отсюда
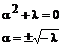
И в результате общее решение имеет вид
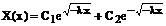
Из граничных условий

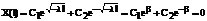
Из первого уравнения находим  , подставляем во второе
, подставляем во второе 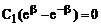
Отсюда получаем 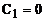 , тогда
, тогда 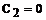 .
.
Таким образом, мы показали, что при λ<0 задача не имеет нетривиальных решений.
2.
λ=0. в этом случае тоже не возникает нетривиальных решений.
3.
λ>0. В этом случае общее решение имеет вид

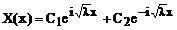
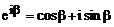
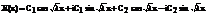

Из граничных условий находим 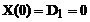

Отсюда 
 ,
,
Где n любое целое число.
Таким образом нетривиальные решения нашей задачи возможны лишь при значениях

Таким образом, мы нашли собственные значения, им будут соответствовать собственные функции

Здесь 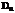 - произвольная постоянная. Найденным собственным значениям соответствует решение уравнения для T:
- произвольная постоянная. Найденным собственным значениям соответствует решение уравнения для T:

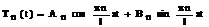 (79)
(79)
Здесь  и
и 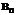 - произвольные постоянные. Таким образом, мы нашли частные решения исходного уравнения колебаний струны:
- произвольные постоянные. Таким образом, мы нашли частные решения исходного уравнения колебаний струны:
 (80)
(80)
или
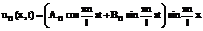 (81)
(81)
Очевидно, что сумма частных решений также будет удовлетворять исходному уравнению и граничным условиям:
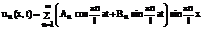 (82)
(82)
Неизвестные константы надо определить из начальных условий:
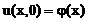 ,
,  (83)
(83)
 Т.е.,
Т.е.,
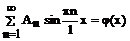 (84)
(84)
 (85)
(85)
Формулы (84) и (85) представляют из себя разложения функций 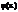 и
и 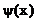 в ряд Фурье. Для нахождения неизвестных констант умножим левую и правую части уравнения (84) на
в ряд Фурье. Для нахождения неизвестных констант умножим левую и правую части уравнения (84) на  и проинтегрируем их по dx от 0 до l:
и проинтегрируем их по dx от 0 до l:
 (86)
(86)
Для вычисления интеграла в левой части последнего равенства воспользуемся тригонометрической формулой

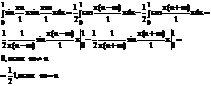 Таким образом,
Таким образом,
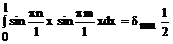 (87)
(87)
Подставляя (87) в (86), получаем
 (88)
(88)
Аналогично для  получаем
получаем
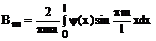 (89)
(89)
