Экономико-математические методы

Э-М модель — описание, отображающее экономический процесс или явление с помощью математических выражений (уравнений, f-ий, неравенств, тождеств), имитирующих поведение моделируемого объекта в заданных или возможных условиях его реального существования.

Принятие типовых решений на основе экономико-математических моделей базируется на методах имитационного моделирования, линейного программирования, вероятностного моделирования, исследования операций и др.

Группы:

- методы оптимизации,

- методы, учитывающие неопределенность, прежде всего вероятностно-статистические,

- методы построения и анализа имитационных моделей

(Имитационный эксперимент - 6 этапов:

1) формулировка задачи,

2) построение математической модели,

3) составление программы для ЭВМ,

4) оценка пригодности модели,

5) планирование эксперимента,

6) обработка результатов эксперимента).

- методы анализа конфликтных ситуаций (теории игр).

Виды мат. моделей в экономике:

1) ориент. на практ. исп-ие (модели статист. контроля);

2) модели, которые практически использовать невозможно (модели «основного уравнения количественной теории денег»).

+:- теоретические (позвол. изучать общ. св-а экономики и ее характерных элементов дедукцией выводов из формальных предпосылок) и прикладные (возможность оценить параметры f-ия конкр. экономического объекта и подготовить рекомендации для принятия практических решений);

- оптимизационные и равновесные;

- статические (описывается состояние эк. объекта в конкр. момент или период времени) и динамические (вкл. взаимосвязи переменных во времени);

- детерминированные (жесткие f-е связи между переменными) и стохастические (допускают наличие случайных воздействий на исследуемые показатели и используют инструментарий теории вероятностей и математической статистики для их описания).

Процесс моделирования:

I. Ан-з теорет. зак-тей, свойственных изучаемому явлению или процессу, и эмпирических данных о его структуре и особенностях. (!четкая формулировка конечной цели построения модели; определение критерия, по которому будут сравниваться различные варианты решения).

2 Определение методов, с помощью которых можно решить задачу.

3. Анализ полученных результатов и уточнение формы и структуры модели; возвращение на первый этап.

Недостатки моделирования:

- включение в модель несущественных для решаемой задачи показателей и нормативов;

- исключение из модели существенных для данного объекта характеристик и переменных величин;

- неточная оценка параметров моделируемого объекта;

- недостатки в структуре модели, т е. неправильное и неточное опр-ие f-й зависимости принятых критериев от управляющих и связанных переменных;

- чрезмерная упрощенность модели, не полностью охватывающая осн. параметры и переменные объекты в его динамике,

- чрезмерное усложнение модели, затрудняющее анализ переменных и повышающее затраты времени и ресурсов на моделирование.

Статистика объектов нечисловой природы. Анализ результатов измерений по качественным и разнотипным признакам; бинарных отношений (ранжировок, разбиений (классификаций), толерантностей и др.); результатов парных сравнений; векторов из 0 и 1 (люсианов); множеств, нечетких множеств; текстов; как обобщение - элементов пространств произвольной природы, в которых нет линейной структуры, но есть метрика или показатель различия. Сводка основных подходов и результатов статистики объектов нечисловой природы, или статистики нечисловых данных, дана в монографиях, сборнике статей. Одно из основных применений статистики объектов нечисловой природы - теория и практика экспертных оценок, связанные с теорией статистических решений и проблемами голосования.

Теория конфликтных ситуаций (теория игр). Зародилась как теория рационального поведения двух игроков с противоположными интересами. Она наиболее проста, когда каждый из них стремится минимизировать свой средний проигрыш, т.е. максимизировать свой средний выигрыш. Участники конфликта могут оценивать свой риск по иным критериям. В случае нескольких игроков возможны коалиции. Большое значение имеет устойчивость точек равновесия и коалиций.

Содержание моделирования и типы применяемых моделей

Модель - условный образ объекта исследования, отображающий его характеристики: свойства, взаимосвязи, структурные и f-ые параметры, значимые для цели исследования .

Типы:

Физическая (материальная) (сохраняет физ. природу объекта: испытательные стенды для проверки качеств. характеристик материалов и конструкций; макеты сооружений; специф. вид - имитационные (деловые управленческие игры, тренинги).

«+»: наглядность, надежность результатов наблюдения, возможности корректирования. «-»: сложность орг-ции осуществления модели, потребность в одновременном использовании значительного числа испытаний, значительные затраты на создание уникальных моделей с опр. производственными ситуациями.

Абстрактные (позволяют описать объект на каком - либо формальном языке в виде чисел, графиков, диаграмм, рисунков).

- графические, текстовые, логические (в виде текста, матриц графических схем, сетей, в которых указываются логические операции в определенной последовательности), математические, электронные или машинные (в виде алгоритма).

Моделирование - конструирование модели на основе предв. изучения хар-ик объекта.

Управляемые переменные - факторы, на которые может оказывать влияние руководитель предприятия (численность работников и т.д.). Неуправляемые - факторы, на которые невозможно воздействовать (поведение поставщиков и др.).

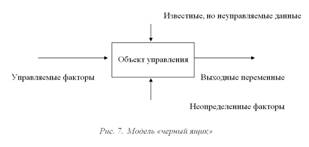Содержание процесса разработки решения сводится к поиску оптимального решения, в наибольшей степени соответствующего заданному критерию. Достигается это составлением альтернатив решений, рассчитанных для конкретных состояний переменных факторов (условий внешней среды).

Этапы построения модели:

1) постановка задачи,

2) построение,

3) проверка на достоверность, применение и обновление модели (все ли существенные компоненты реальной ситуации встроены в модель).