К.т.н., профессор Д.П.Барков, МИИГАиК

Р.Ш. СУФИЯНОВ

О.О. ГОРБЕНКО

Элементы

системного анализа

Федеральное агентство по образованию

Московский государственный университет

инженерной экологии

Р.Ш. СУФИЯНОВ

О.О. ГОРБЕНКО

Элементы

системного анализа

Учебное пособие

Москва

МГУИЭ

2009

УДК 517.9

ББК 35.11

С90

Рецензенты: кафедра «Гостиничный и туристический бизнес» РЭА

им. Г.В.Плеханова

К.т.н., профессор Д.П.Барков, МИИГАиК

Допущено редакционно-издательским советом МГУИЭ

Суфиянов Р.Ш.

С90 Элементы системного анализа: Учебное пособие
/Р.Ш. Суфиянов, О.О Горбенко.― М.: МГУИЭ, 2009 ― 52 с.

ISBN 978-5-9513-0183-3

В учебном пособии рассматриваются задачи математического и физического моделирования химико-технологических систем.

Предназначено студентам всех специальностей дневной и вечерней форм обучения при изучении дисциплины «Введение в системный анализ».

УДК 517.9

ББК 35.11

ISBN 978--5-9513-0183-3

© Р.Ш. Суфиянов, О.О. Горбенко, 2009

© МГУИЭ, 2009

Теория подобия и p-теорема

Теория подобия является учением об условиях подобия физических явлений. Методы теории подобия лежат в основе масштабирования и моделирования процессов.

Процессы подобны, если они описываются одним и тем же дифференциальным уравнением (или системой дифференциальных уравнений) при подобных условиях однозначности, включающих геометрическое подобие систем, временнòе подобие, подобие физических величин, характеризующих процесс, подобие граничных и начальных условий.

Условия однозначности, заданные в виде конкретных численных значений, выделяют из всего класса процессов, описываемых данным дифференциальным уравнением, один конкретный процесс. Таким образом, условия однозначности — это
индивидуальные признаки различных процессов одного и того же класса.

Понятие подобия процессов значительно шире понятия подобия условий однозначности.

Из дифференциальных уравнений получают безразмерные величины — инварианты подобия, подразделяемые на
симплексы и комплексы.

Симплексы образованы из однородных (по размерности)
величин, к таким, например, относится геометрический
симплекс (параметрическое число подобия Г):

,

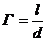где d — линейный размер (диаметр), м;

l — линейный размер (длина), м.

Комплекс образован величинами, разнородными по размерности. Примерами комплексов являются числа (критерии) подобия, например, число Рейнольдса:

,

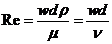где w — скорость потока жидкости (газа), м·с^–1;

r — плотность жидкости (газа), кг·м^–3;

m — динамический коэффициент вязкости жидкости
(газа), Па·с;

ν — кинематический коэффициент вязкости жидкости

(газа), м²·с^–1;

или число Нуссельта:

,

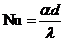где a — коэффициент теплоотдачи, Вт×м^–2×К^–1;

l — коэффициент теплопроводности, Вт×м^–1×К^–1;

или же число Эйлера

,

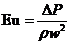где DР — перепад давлений (гидравлическое сопротивление), Па;

r — плотность жидкости (газа), кг×м^–3 ;

w — скорость потока жидкости (газа), м·с^–1.

Если числа подобия находят из условий однозначности,
то они носят название определяющих чисел подобия. Равенство определяющих чисел (критериев) подобия является условием подобия процессов. Числа подобия, содержащие хотя бы
одну физическую величину, не включённую в условия однозначности, называют определяемыми (неопределяющими) числами подобия. Их равенство является следствием подобия процессов.

Практическое применение теории подобия к экспериментальному и теоретическому исследованию процессов основано на следующих теоремах подобия.

Теорема подобия (Ньютона-Бертрана): подобные явления характеризуются численно равными критериями подобия.

Теорема подобия (Кирпичёва-Гухмана): подобны те явления или системы, которые описываются одинаковыми уравнениями связи, и условия однозначности у которых подобны.

Теорема подобия (Бекингема—Федермана):

Любая зависимость вида

f(х₁, х₂, …, х_n) = 0 или х₁ = f(х₂, х₃, …, х_n) (1)

между n характеризующими систему физическими величинами х можно представить как зависимость между безразмерными величинами в виде уравнения подобия (критериального уравнения) вида

f(p₁, p₂, …, p_i) = 0 или p₁(х₁) = f(p₂, …, p_i), (2)

где p — безразмерные величины (числа подобия);

i — количество безразмерных величин;

х — физические величины;

n — количество физических величин.

Здесь p₁ — определяемое число подобия; p₂, …, p_i – определяющие числа подобия.

Или, иными словами, функциональная зависимость между характеризующими процесс величинами может быть представлена в виде зависимости между составленными из них критериями подобия (критериальной зависимости).

Применять теорию подобия можно лишь, когда удается
составить дифференциальное уравнение, описывающее изучаемый процесс, и сформулировать условия однозначности. Однако
в некоторых случаях при изучении сложных процессов, явлений, зависящих от большого числа самых различных факторов, не удается составить даже дифференциальных уравнений, которые описывали бы эти сложные явления или процессы. В таких случаях математически возможно лишь представить зависимости между величинами в самом общем виде, а именно —
неопределенной функцией искомой величины от величин, на неё влияющих. Эту функциональную зависимость, составленную из физических величин, можно показать в виде
степенного уравнения вида

x₁ = A x₂^a x₃^b x₄^c x₅^d … x_n^z, (3)

где А, a, b, …, z — безразмерные коэффициент и показатели
степени.

Связь между различными физическими факторами можно
установить лишь методом анализа размерностей,позволяющим привести функциональную зависимость самого общего вида
к строго определенному числу безразмерных комплексов физических величин, а при наличии подобия — к строго определенному числу инвариантов подобия. В основе этого метода лежит понятие размерности (физической величины), под которой понимается представление её в виде зависимости от основных единиц системы измерения СИ (табл. 1).

Для выявления обобщенных зависимостей между физическими величинами, конкретный вид связи между которыми
неизвестен, служит p-теорема анализа размерностей, позволяющая найти количество чисел подобия, входящих в искомое уравнение подобия для исследуемого процесса.

Формулировка p-теоремы

Если общая функциональная зависимость вида (1) связывает n размерных величин, которые выражают через m основных единиц системы измерения, то эта зависимость может быть сведена к уравнению подобия (2), содержащему i безразмерных величин

i = n – m, (4)

где i — число безразмерных величин;

n — число физических величин в (1),

m — число основных единиц системы измерений, через
которые выражены эти величины.

Таблица 1

Основные физические величины, символы,

размерности и единицы СИ

Величина	Единица СИ
Наименование	Обозна-чение	Раз-мерность	Наимено-вание	Обозначение
Между-нар.	На рус. яз.
Время	t	T	секунда	s	c
Длина	l	L	метр	m	м
Кол-во вещества	n	N	моль	mol	моль
Масса	m	M	килограмм	kg	кг
Сила света	J	J	канделла	kd	кд
Сила эл. тока	I	I	ампер	А	А
Темпера-тура	Т	Θ	кельвин	К	К

Следствие p-теоремы

Если среди n величин в зависимости (1) имеется q неоднородных величин (т. е. величин с неоднородными размерностями), то количество симплексов S составляет

S = n – q, (5)

а количество комплексов К составляет

K = q – m. (6)

Здесь, как и в (4), m — количество основных единиц системы единиц измерений СИ, установленной в настоящее время для научно-технической документации. Основные (независимые) единицы этой системы приведены в табл. 1.

В отличие от основных, производные единицы системы измерений — это единицы производных величин, определяемые по уравнениям связи с единицами других величин.

Определим единицу измерения динамического коэффициента вязкости m, выразив его размерность сначала через производные, а затем основные единицы СИ:

[m] = Па·с = (H·м^–2)·с = ((кг·м·с^–2)·м^–2)·с = кг·м^–1·с^–1.

Задача

Условие

Определить потери DР давления на преодоление сопротивления трению изотермическим (Т = const) потоком вязкой не-сжимаемой жидкости в условиях установившегося ламинарного режима течения в круглой прямой горизонтальной трубе диаметром d на участке длиной l , если функциональная зависимость (1) имеет вид

DР = DР (m, w, d, l), (7)

где w — скорость потока.

Решение

1) Считаем количество n физических величин в зависимости (7).

n = 5.

2) Определяем количество основных единиц СИ, через
которые выражены эти величины, для чего выпишем формулы размерности каждой из величин в зависимости (7):

[DР] = Па = Н·м^–2 = (кг·м·с^–2 )·м^–2 = кг·м^–1·с^–2 =

= М·L^–1·T^–2;

Следовательно, m = 3 (кг, м, с);

[m] = [M L^–1 T^–1];

[w] = м·с^–1 = [L·T^–1];

[d] = м = [L];

[l] = м = [L].

3) Определяем количество q величин с неодинаковой размерностью

q = 4, это DP, m, w, d.

4) Из (4) находим число инвариантов в искомом уравнении подобия

i = n – m = 5 – 3 = 2.

В том числе:

количество симплексов согласно (5)

S = n – q = 5 – 4 = 1;

количество комплексов согласно (6)

K = q – m = 4 – 3 = 1.

5) Представим функциональную зависимость (7) в виде степенного уравнения

DР = Аm^Bw^Cd^D l^E. (8)

6) Подставим формулы размерности физических величин
в степенное уравнение (8)

[M^.L^–1.T^–2 ] = A[M^.L^–1.T^–1]^B.[L^.T^–1]^C.[L]^D.[L]^E.

Раскрывая скобки в правой части последнего уравнения,
получим:

[M^.L^–1.T^–2 ] = A M^B.L^–B+C+D+E.T^–B–C.

Поскольку А — безразмерный коэффициент, а размерности основных величин независимы, то для того чтобы полученное равенство удовлетворялось, необходимо равенство показателей степеней при одних и тех же единицах измерения в левой и правой частях равенства были равны. Следовательно, для показателей степеней размерностей основных величин получим систему уравнений:

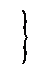[M] 1 = 1·B

[L] –1 = (–1)·B + 1·C + D + E

[T] –2 = (–1)·B + (–1)·C

Решая полученную систему уравнений, определяем значения показателей степеней:

B = 1

C = 2 – B = 1

D = – 1 + B – C – E = –1 – E.

6) Подставив в (8) эти значения показателей степеней, по-лучим:

DР = Am w d^–1 d^–E l^E = A 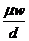( 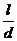)^E

или в соответствии с (2)

p₁ (DР) = Аp₂^E,

где p₁ = 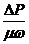, p₂ = 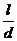= Г.

Итак, зависимость из 5-ти величин преведена к зависимости безразмерных комплекса и симплекса, причем полученный составной комплекс, состоит из произведения хорошо известных чисел подобия: Re и Eu.

С учетом этого критериальное уравнение имеет следующий вид

Eu = ARe^–1Г^Е.

Последующая работа состоит в определении значений показателей степеней и безразмерного коэффициента А, которые находятся на основании опытных данных, как правило, экспериментально-статистическими методами.

Библиографический список

1. Алабужев П.М., Геронимус В.Б., Минкевич Л.М., Шеховцов Б.А. Теории подобия и размерностей. Моделирование. —
М.:Высшая школа, 1968. —206 с.

2. Романков П.Г., Курочкина М.И. Гидромеханические
процессы химической технологии. — Л.: Химия, 1974. —288с.

Варианты заданий

Составить критериальные уравнения, если исходная функциональная зависимость имеет вид:

1. ΔP = f (ρ, w, d, l)

2. ΔP = f (ρ, μ, w, d, l)

3. ΔP = f (ρ, μ, w, g, d, l)

4. α = f (w, ρ, μ, λ, d)

5. α = f (w, ρ, μ, λ, c, d)

6. β = f (D, μ, ρ, l)

7. R = f (l, w, ρ, μ, g),

где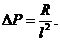

λ — коэффициент теплопроводности, Дж×м^–1×с^–1×град^–1,

Вт×м^–1×К^–1;

α — коэффициент теплоотдачи, Вт×м^–2×К^–1;

c — удельная теплоёмкость, Дж×кг^–1×К^–1;

μ — коэффициент динамической вязкости, Па×с;

ρ — плотность, кг×м^–3;

β — коэффициент массоотдачи, м×с^–1;

D — коэффициент диффузии, м²×с^–1;

g — ускорение свободного падения, м×с^–2;

R — сила сопротивления, Н.

Число Прандтля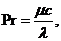

число Нуссельта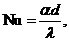

число Фруда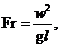

диффузионное число Нуссельта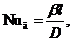

диффузионное число Прандтля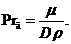

Практическое применение

Библиографический список

1. Кузнецов Ю.Н., Кузубов В.И., Валощенко А.Б. Математическое программирование. — М.: Высшая школа, 1976. 352с.

2. Ларин Р. М., Плясунов А. В., Пяткин А. В. Методы опти мизации. Примеры и задачи. —Учебное пособие. Новосибирск: Новосибирский государственный университет, 2003. 120 с.

Варианты заданий

В 1

Целевая функция Р= 8х₁ + 3х₂ Þ max

Ограничительные условия

х₁ – х₂ £ 4

5х₁+ 4х₂ £ 80

х₁ + 2х₂ £ 32

В 2

Целевая функция Р= 3х₁ + 10х₂ Þ max

Ограничительные условия

х₁ – 2х₂ £ 6

10х₁+ 7х₂ £ 70

х₁ + 2х₂ £ 16

В 3

Целевая функция Р= 5х₁ + 4х₂ Þ max

Ограничительные условия

х₁ + 2х₂ £ 16

10х₁+ 7х₂ £ 70

х₁ – 2х₂ £ 4

В 4

Целевая функция Р= 2х₁ + 9х₂ Þ max

Ограничительные условия

2х₁ – х₂ £ 8

10х₁+ 7х₂ £ 70

х₁ + 3х₂ £ 24

В 5

Целевая функция Р= х₁ + 9х₂ Þ max

Ограничительные условия

2х₁ – х₂ £ 10

5х₁+ 4х₂ £ 80

х₁ + 2,3х₂ £ 32

В 6

Целевая функция Р= 7х₁ + 3х₂ Þ max

Ограничительные условия

х₁ – 2х₂ £ 4

5х₁+ 4х₂ £ 40

10х₁ + 5х₂ £ 65

В 7

Целевая функция Р= 4х₁ + 9х₂ Þ max

Ограничительные условия

х₁ – 2х₂ £ 6

10х₁+ 9х₂ £ 90

х₁ + 2х₂ £ 16

В 8

Целевая функция Р= 8х₁ + 3х₂ Þ max

Ограничительные условия

х₁ – 2х₂ < 4

10х₁+ 7х₂ £ 70

х₁ + 2х₂ £ 10

В 9

Целевая функция Р= х₁ + 9х₂ Þ max

Ограничительные условия

10х₁ + 2х₂ £ 70

2х₁ – х₂ > 8

х₁ + 3х₂ £ 24

В 10

Целевая функция Р= 10х₁ + 3х₂ Þ max

Ограничительные условия

5х₁ + 4х₂ £ 48

2х₁ – х₂ < 10

х₁ + 3х₂ £ 30

В 11

Целевая функция Р= 3х₁ + 7х₂ Þ max

Ограничительные условии

х₁ – х₂ £ 4

5х₁+ 4х₂ £ 80

х₁ + 1,5х₂ £ 21

В 12

Целевая функция Р= 10х₁ + 4х₂ Þ max

Ограничительные условия

10х₁ + 7х₂ £ 70

х₁ – 2х₂ £ 4

х₁ + 2х₂ £ 16

В 13

Целевая функция Р= 4х₁ + 9х₂ Þ max

Ограничительные условия

10х₁ + 7х₂ £ 70

х₁ – 2х₂ £ 4

х₁ + 2х₂ £ 16

В 14

Целевая функция Р= 4х₁ + 8,5х₂ Þ max

Ограничительные условия

х₁ + 4х₂ £ 14

3х₁+ 4х₂ £ 18

6х₁ + 2х₂ £ 27

В 15

Целевая функция Р= х₁ + 8х₂ Þ max

Ограничительные условия

2х₁ – х₂ £ 10

5х₁+ 4х₂ £ 80

х₁ + 2х₂ £ 30

В 16

Целевая функция Р= 2х₁ + 9х₂ Þ max

Ограничительные условия

х₁ – х₂ £ 4

5х₁ + 4х₂ £ 60

х₁ + 1,5х₂ £ 21

В 17

Целевая функция Р= 3х₁ + 10х₂ Þ max

Ограничительные условия

2х₁ – 2х₂ £ 6

10х₁+ 2х₂ £ 70

х₁ + 4х₂ £ 45

В 18

Целевая функция Р= 5х₁ + 4х₂ Þ max

Ограничительные условия

х₁ – 2х₂ £ 4

10х₁+ 7х₂ £ 70

х₁ + 2х₂ £ 10

В 19

Целевая функция Р= 5х₁ + 4х₂ Þ max

Ограничительные условия

х₁ +2х₂ £ 32

10х₁+ 4х₂ £ 80

х₁ – 23х₂ £ 4

В 20

Целевая функция Р= 3х₁ + 5х₂ Þ max

Ограничительные условия

х₁ – х₂ £ 3

х₁+ х₂ £ 10

3х₁ +9х₂ £75

В 21

Целевая функция Р= 5х₁ + 4х₂ Þ max

Ограничительные условия

х₁ +2х₂ £ 28

10х₁+ 2х₂ £ 52

3х₁ – 2х₂ £ 4

В 22

Целевая функция Р= 3х₁ + 7х₂ Þ max

Ограничительные условия

х₁ – х₂ £ 10

5х₁+ 4х₂ £ 90

х₁ + 2х₂ £ 40

В 23

Целевая функция Р= 10х₁ + 3х₂ Þ max

Ограничительные условия

4х₁ + 3х₂ £ 30

2х₁ – х₂ £ 10

х₁ + 4х₂ £ 24

В 24

Целевая функция Р= 5х₁ + 7х₂ Þ max

Ограничительные условия

4х₁ + 3х₂ £ 30

2х₁ – х₂ £ 8

х₁ + 4х₂ £ 24

В 25

Целевая функция Р= 8х₁ + 3х₂ Þ max

Ограничительные условия

6х₁ – 3х₂ £ 4

6х₁ + х₂ £ 40

х₁ + 2х₂ £ 40

Структурная схема

На основе технологической схемы построим структурную схему процесса. Аппараты в такой схеме изображают прямоугольниками, которые, по необходимости, располагают либо по горизонтали, либо по вертикали, либо, в случае сложной схемы, друг под другом.

Рис. 3. Структурная схема процесса

Топологическая схема

(топологический граф)

В топологической схеме аппараты изображают жирной точкой (вершиной), а потоки — линией или дугой.

Рис. 4. Топологический граф процесса

Далее можно составить материальный баланс, используя топологический граф.

Составим матрицу инциденций, для чего сначала введем
числовой код [S_ij], где i — номер строки (аппараты); j —, номер столбца (потоки).

–1, если дуга q_j выходит из вершины i-го типа

S_ij = +1, если дуга q_j входит в вершину i-го типа

0, если дуга q_j не инцидентна вершине i-го типа*.

*Не входит в вершину и не выходит из неё.

Матрица инциденций

i/j

+1

–1

–1

+1

Sij =

+1

–1

+1

–1

+1

–1

+1

–1

+1

–1

+1

–1

Составим материальный баланс с помощью матрицы
инциденций и матрицы расхода.

Введем обозначения:

m_j — массовый расход j-го потока;

x_kj — массовая концентрация k-го компонента в j-м потоке;

m_j*x_kj — массовый расход k -го компонента в j-м потоке,

где k — номер компонента.

Построим матрицу покомпонентного состава потока (матрицу расхода). Пусть число компонентов в каждом потоке k = 3.

Матрица расходов

	i/j				…
		m1x11	m2x12	m3x13	…	m8x18	m9x19
[MjXkj] =		m1x21	m2x22	m3x23	…	m8x28	m9x29
		m1x31	m2x32	m3x33	…	m8x38	m9x39

Теперь у нас есть две матрицы: инциденций и расходов. Составим материальный баланс для первого аппарата и первого компонента, участвующего в потоке. Перемножим соответствующие строки матриц, затем сложим элементы матрицы, приравняем сумму нулю и таким образом получим материальный баланс.

Для i = 1 и k =1, т.е. первого аппарата и первого компонента получим:

[S_ij]*[M_jX_kj] =[m₁x₁₁ – m₂x₁₂ – m₃x₁₃ + m₇x₁₇] = 0.

Библиографический список

1. Шатихин Л.Г. Структурные матрицы и их применение для исследования систем. — М.: Машиностроение, 1974. —248с.

2. Голуб Дж., Ван Лоун Ч. Матричные вычисления. — М.: Мир, 1999. —548с.

Задание

Построить структурную схему и топологический граф для ХТС производства промышленного этилового спирта из этилена (схема задана).

Составить матрицу инциденций и показать ее применение на примере составления материального баланса для аппарата a = и компонента k = .

Рис. 5. Схема получения этилового спирта из этилена:

1 — смеситель; 2 — трубчатый теплообменник; 3 —трубчатая печь; 4 — реактор; 5 — сборный сепаратор;6 — холодильник;7 — абсорбер;8 — дополнительный сборник.

q₁ — этилен; q₂ —вода; q₃ —циркулирующий поток; q₄ ,

q₅ — газовая смесь; q₆ — парогазовая смесь; q₇, q₈ —реакционная смесь; q₉, q₁₁ — газовая фаза; q₁₀ — жидкая фаза; q₁₂ —абсорбент; q₁₃, q₁₄ — водный спирт; q₁₅, q₁₆ —охлаждающая вода.

Варианты заданий

Номер варианта	Номер аппарата	Номер компонента

Библиографический список

1. Кафаров В.В. Методы кибернетики в химии и химической технологии. — М.: Химия, 1976. —464с.

2. Бондарь А.Г. Математическое моделирование в химической технологии. — Киев: Вища школа, 1973. —280 с.

Значения критерия Фишера

f2*	Число степеней свободы
	161,4	199,5	215,7	224,6	230,2	234,0
	18,51	19,00	19,16	19,25	19,30	19,33
	10,13	9,55	9,28	9,12	9,01	8,94
	7,71	6,94	6,59	6,39	6,26	6,16
	6,61	5,79	5,41	5,19	5,05	4,95
	5,99	5,14	4,76	4,53	4,39	4,28
	5,59	4,74	4,35	4,12	3,97	3,87
	5,32	4,46	4,07	3,84	3,69	3,58
	5,12	4,26	3,86	3,63	3,48	3,37
	4,96	4,10	3,71	3,48	3,33	3,22
	4,84	3,98	3,59	3,36	3,20	3,09
	4,75	3,88	3,49	3,26	3,11	3,00
	4,67	3,80	3,41	3,18	3,02	2,92
	4,60	3,74	3,34	3,11	2,96	2,85
	4,54	3,68	3,29	3,06	2,90	2,79
	4,49	3,63	3,24	3,01	2,85	2,74
	4,35	3,49	3,10	2,87	2,71	2,60
	4,17	3,32	2,92	2,69	2,53	2,42
	4,08	3,23	2,84	2,61	2,45	2,34
	4,03	3,18	2,79	2,56	2,40	2,29
	3,94	3,09	2,70	2,46	2,30	2,19
∞	3,84	2,99	2,60	2,37	2,21	2,09

*f₂ — число степеней свободы для меньшей дисперсии

ПРИЛОЖЕНИЕ 1

для уровня значимости α = 0,05

f1 для большей дисперсии
						∞
238,9	243,9	246,5	249,0	251,8	253,3	254,0
19,37	19,41	19,43	19,45	19,47	19,49	19,50
8,84	8,74	8,69	8,64	8,58	8,56	8,53
6,04	5,91	5,84	5,77	5,70	5,66	5,63
4,82	4,68	4,60	4,53	4,44	4,40	4,36
4,15	4,00	3,92	3,84	3,75	3,71	3,67
3,73	3,57	3,49	3,41	3,32	3,28	3,23
3,44	3,28	3,20	3,12	3,03	2,98	2,93
3,23	3,07	2,98	2,90	2,80	2,76	2,71
3,07	2,91	2,82	2,74	2,64	2,59	2,54
2,95	2,79	2,70	2,61	2,50	2,45	2,40
2,85	2,69	2,60	2,50	2,40	2,35	2,30
2,77	2,60	2,51	2,42	2,32	2,26	2,21
2,70	2,53	2,44	2,35	2,24	2,19	2,13
2,64	2,48	2,39	2,29	2,18	2,12	2,07
2,59	2,42	2,33	2,24	2,13	2,07	2,01
2,45	2,28	2,28	2,08	1,96	1,90	1,84
2,27	2,09	1,99	1,89	1,76	1,69	1,62
2,18	2,00	1,90	1,79	1,66	1,59	1,51
2,13	1,95	1,85	1,74	1,60	1,52	1,44
2,03	1,85	1,75	1,63	1,48	1,39	1,28
1,94	1,75	1,64	1,52	1,35	1,24	1,00

Содержание

Теория подобия и π-теорема........................................... 3

Варианты заданий.......................................................... 12

Практическое применение метода
линейного программирования...................................... 14

Варианты заданий.......................................................... 20

Матричное представление

структуры химико-технологических систем............... 25

Варианты заданий.......................................................... 30

Моделирование методом «чёрного ящика»................. 31

Варианты исходных данных к заданиям...................... 41

Приложения............................................................ 45

Учебное издание

Суфиянов Ракип Шайхиевич

Горбенко Ольга Олеговна

ЭЛЕМЕНТЫ СИСТЕМНОГО АНАЛИЗА

Компьютерная вёрстка: А.Г. Ланцетти

Подписано в печать 12.01.09. Форм.бум. 60´84 1/16.

Усл. печ. л. 3,2. Уч.-изд. л. 3,25. Тираж 150 экз.

МГУИЭ, издательский центр

105066, Москва, ул. Старая Басманная, 24/1

Р.Ш. СУФИЯНОВ

О.О. ГОРБЕНКО

Элементы

системного анализа

Федеральное агентство по образованию

Московский государственный университет

инженерной экологии

Р.Ш. СУФИЯНОВ

О.О. ГОРБЕНКО

Элементы

системного анализа

Учебное пособие

Москва

МГУИЭ

2009

УДК 517.9

ББК 35.11

С90

Рецензенты: кафедра «Гостиничный и туристический бизнес» РЭА

им. Г.В.Плеханова

к.т.н., профессор Д.П.Барков, МИИГАиК

Допущено редакционно-издательским советом МГУИЭ

Суфиянов Р.Ш.

С90 Элементы системного анализа: Учебное пособие
/Р.Ш. Суфиянов, О.О Горбенко.― М.: МГУИЭ, 2009 ― 52 с.

ISBN 978-5-9513-0183-3

В учебном пособии рассматриваются задачи математического и физического моделирования химико-технологических систем.

Предназначено студентам всех специальностей дневной и вечерней форм обучения при изучении дисциплины «Введение в системный анализ».

УДК 517.9

ББК 35.11

ISBN 978--5-9513-0183-3

© Р.Ш. Суфиянов, О.О. Горбенко, 2009

© МГУИЭ, 2009

Теория подобия и p-теорема

Теория подобия является учением об условиях подобия физических явлений. Методы теории подобия лежат в основе масштабирования и моделирования процессов.

Процессы подобны, если они описываются одним и тем же дифференциальным уравнением (или системой дифференциальных уравнений) при подобных условиях однозначности, включающих геометрическое подобие систем, временнòе подобие, подобие физических величин, характеризующих процесс, подобие граничных и начальных условий.

Условия однозначности, заданные в виде конкретных численных значений, выделяют из всего класса процессов, описываемых данным дифференциальным уравнением, один конкретный процесс. Таким образом, условия однозначности — это
индивидуальные признаки различных процессов одного и того же класса.

Понятие подобия процессов значительно шире понятия подобия условий однозначности.

Из дифференциальных уравнений получают безразмерные величины — инварианты подобия, подразделяемые на
симплексы и комплексы.

Симплексы образованы из однородных (по размерности)
величин, к таким, например, относится геометрический
симплекс (параметрическое число подобия Г):

,

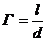где d — линейный размер (диаметр), м;

l — линейный размер (длина), м.

Комплекс образован величинами, разнородными по размерности. Примерами комплексов являются числа (критерии) подобия, например, число Рейнольдса:

,

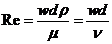где w — скорость потока жидкости (газа), м·с^–1;

r — плотность жидкости (газа), кг·м^–3;

m — динамический коэффициент вязкости жидкости
(газа), Па·с;

ν — кинематический коэффициент вязкости жидкости

(газа), м²·с^–1;

или число Нуссельта:

,

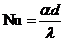где a — коэффициент т