Прямоугольная система координат на плоскости.

Прямоугольная система координат на плоскости.

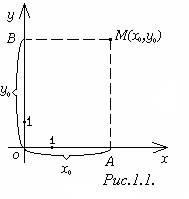Две взаимно перпендикулярные оси Ох и Оу, имеющие общее начало О и одинаковую масштабную единицу (рис.1.1), образуют прямоугольную (декартову) систему координат на плоскости.Ось Ох называется осью абсцисс, ось Оу ─ осью ординат, а обе оси вместе ─ осями координат. Точка О пересечения осей называется началом координат. Плоскость, в которой расположены оси Ох и Оу, называется координатной плоскостьюи обозначается Оху.

Пусть М ─ произвольная точка плоскости. Опустим из неё перпендикуляры МА и МВ на оси Ох и Оу. Точке М на плоскости ставят в соответствие два числа:

­­­– абсциссу х_0, равную расстоянию от О до А, взятому со знаком «+», если А лежит правее О, и со знаком «-», если А лежит левее О;

– ординату у₀, равную расстоянию от точки О до В, взятому со знаком «+», если В лежит выше О, и со знаком «-», если В лежит ниже О.

Абсцисса и ордината точки М называются прямоугольными (декартовыми) координатами точки М.Запись М(х₀;у₀) означает, что точка М имеет абсциссу, равную х₀, и ординату, равную у₀.

Введение прямоугольной системы координат на плоскости позволяет установить взаимно однозначное соответствие между множеством всех точек плоскости и множеством пар чисел, что даёт возможность при решении геометрических задач применять алгебраические методы.

Полярная система координат.

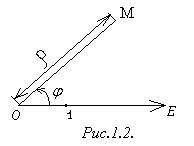Полярная система координатсостоит из некоторой точки О, называемой полюсом, и исходящего из неё луча ОЕ ─ полярной оси. Кроме того, задаётся единица масштабадля измерения длин отрезков.

Пусть задана полярная система координат и пусть М - произвольная точка плоскости. Пусть r ─ расстояние от М до полюса О; j ─ угол, на который надо повернуть против часовой стрелки полярную ось для совмещения с лучом ОМ (рис.1.2).

Полярными координатами точки Мназываются числа r и j. При этом число r считается первой координатой и называется полярными радиусами,число j ─ второй координатой и называется полярным углом. Точка М с полярными координатами r и j обозначается М(r;j), причём 0≤r<+∞, 0≤j<2p. Однако в ряде случаев приходится рассматривать углы, большие 2p, а также отрицательные углы, т.е. отсчитываемые от полярной оси по часовой стрелке. Полюсу О соответствует полярный радиус r= 0, а полярный угол для него не определён.

Площадь треугольника.

Теорема 1.3.Для любых точек А(х₁;у₁), В(х₂;у₂) и С(х₃;у₃), не лежащих на одной

прямой, площадь S треугольника АВС выражается формулой

S = ô(х₂ – х₁)(у₃ – у₁) – (х₃ – х₁)(у₂ – у₁)ô. (6)

Доказательство.Площадь ∆ АВС, изображённого на рис.1.7, вычисляем следующим образом:

S_ABC = S_ADEC + S_BCEF – S_ABFD.

Вычисляем площади трапеций:

S_ADEC = ,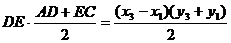

S_BCEF = ,

S_ABFD = .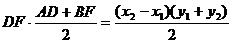

Теперь имеем

S_ABC = ((х₃ – х₁)(у₃ + у₁) + (х₂ – х₃)(у₃ + у₂) - (х₂ –

– х₁)(у₁ + у₂)) = (х₃у₃ – х₁у₃ + х₃у₁ – х₁у₁+ х₂у₃ –

– х₃у₃ + х₂у₂ – х₃у₂ – х₂у₁ + х₁у₁ – х₂у₂ + х₁у₂) =

= (х₃у₁ – х₃у₂ + х₁у₂ – х₂у₁ + х₂у₃ – х₁у₃) = (х₃(у₁ – у₂) + х₁у₂ – х₁у₁ + х₁у₁ – х₂у₁ + у₃(х₂ – – х₁)) = (х₁(у₂ – у₁) – х₃(у₂ – у₁) + у₁(х₁ – х₂) – у₃(х₁ – х₂)) = ((х₁ – х₃)(у₂ – у₁) + (х₁ –

– х₂)(у₁ – у₃)) = ((х₂ – х₁)(у₃ – у₁) – (х₃ – х₁)(у₂ – у₁)).

Для другого расположения ∆ АВС формула (6) доказывается аналогично, но может получиться со знаком «-». Поэтому в формуле (6) ставят знак модуля.

Примеры уравнений линий на плоскости.

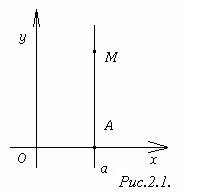1) Рассмотрим прямую, параллельную оси Oy прямоугольной системы координат (рис.2.1). Обозначим буквой A точку пересечения этой прямой с осью Ox, (a,o) ─ её координаты. Уравнение x = a является уравнением данной прямой. Действительно, этому уравнению удовлетворяют координаты любой точки M(a,y) этой прямой и не удовлетворяют координаты ни одной точки, не лежащей на прямой. Если a = 0, то прямая совпадает с осью Oy, которая имеет уравнение x = 0.

2) Уравнение x – y = 0 определяет множество точек плоскости, составляющих биссектрисы I и III координатных углов.

3) Уравнение x² - y² = 0 ─ это уравнение биссектрис всех координатных углов.

4) Уравнение x² + y² = 0 определяет на плоскости единственную точку O(0,0).

5) Уравнение x² + y² = 25 ─ уравнение окружности радиуса 5 с центром в начале координат.

Общее уравнение прямой.

Теорема 2.1.Каждая прямая на плоскости с прямоугольной системой координат определяется уравнением первой степени

Ax + By + C = 0, где A и B одновременно не равны 0, (5)

и, обратно, уравнение (5) при произвольных коэффициентах A, B и C (A и B одновременно не равны нулю) определяет некоторую прямую на плоскости.

Доказательство.Сначала докажем первое утверждение. Если прямая не перпендикулярна оси Ox, то она определяется уравнением первой степени y = kx + b или

kx – y + b = 0, т.е. уравнением вида (5), где A = k, B = -1, C = b. Если прямая перпендикулярна оси Ox, то согласно примера 1) из п. 2.2 её уравнение имеет вид x = a или x – a = 0, т.е. является уравнением вида (5) при A = 1, B = 0 и C = -a. Тем самым первое утверждение доказано.

Докажем обратное утверждение. Пусть дано уравнение (5), причём хотя бы один из коэффициентов A или B отличен от нуля. Если, например, B ¹ 0, то уравнение (5) можно записать в виде

y = - 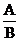x - ,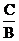

т.е. в виде уравнения с угловым коэффициентом. По п. 2.3 это уравнение определяет на плоскости прямую. Если же B = 0, то A ¹ 0 и уравнение (5) имеет вид x = - 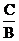. Это уравнение прямой, параллельной оси Oy, как показано в примере 1) п. 2.2. Второе утверждение доказано.

Уравнение первой степени (5) называется общим уравнением прямой на плоскости.

Эллипс. Окружность.

Определение 4.1. Эллипсомназывается множество всех точек плоскости, для каждой из которых сумма расстояний до двух данных точек, называемых фокусами, есть величина постоянная, большая чем расстояние между фокусами.

Пусть F₁(-c,0) и F₂(c,0) ─ фокусы. Тогда F₁F₂ = 2c ─ фокусное расстояние(рис.4.1). Постоянную величину, о которой идёт речь в определении эллипса, обозначим 2a.

Пусть M(x,y) ─ произвольная точка эллипса. Тогда по определению F₁M + F₂M = 2a > 2c, откуда a > c.

Так как F₁M = , F₂M = , то имеем уравнение + = 2a.

Преобразуем это уравнение:

( )² = (2a − )² ,

(x² + 2cx + c²) + y² = 4a² – 4a + (x² –­ 2cx + c²) + y²,

a = a² – cx.

Возводя в квадрат последнее уравнение, имеем

a²(x² – 2cx + c² + y²) = a⁴ – 2cxa² + c²x²,

(a² – c²)x² + a²y² = a²(a² – c²).

Так как a > c, то a² – c² > 0 и можем обозначить b² = a² – c². Тогда

b²x² + a²y² = a²b²,

= 1 (1)

Таким образом, координаты любой точки эллипса удовлетворяют уравнению (1).

Покажем обратное: если координаты точки M(x,y) удовлетворяют уравнению (1), то точка M лежит на эллипсе.

Из (1) найдём y² : y² = b²(1 - ).

Тогда F₁M = = = = = = = │ │

Т.к. c < a и из (1) ≤ 1, т.е. x² ≤ a² , │x│ ≤ a, то . Следовательно,

│ │= .

Аналогично можно вычислить

F₂M = .

Теперь

F₁M + F₂M = .

Из уравнения (1) : b² > 0 Þ a² – c² > 0, т.е. a > c, откуда 2a > 2c. Значит, точка M лежит на эллипсе.

Уравнение (1) называется каноническим уравнением эллипса.Изображён эллипс с уравнением (1) на рис 4.2.

Точки пересечения эллипса с осями координат называются вершинами эллипса.Оси симметрии эллипса (оси Ox и Oy) называют осями эллипса. Точка пересечения осей ─ центр эллипса. Осяминазывают также отрезки A₁A, B₁B. Отрезки OA, OB и их длины называют полуосями. В нашем случае a > b, поэтому а называют большой полуосью,b ─ малой полуосью. Эксцентриситетом эллипсаназывается отношение фокусного расстояния к длине большой оси, т.е.

ε = .

Так как 0 c < a, то 0 ε < 1. Фокальными радиусами точки Mназывают отрезки F₁M и F₂M. Их длины r₁ и r₂ вычисляют по формулам

r₁ = a + εx,

r₂ = a – εx.

Уравнение (1) можно рассматривать и в случае, когда b > a, оно определяет эллипс с большой полуосью OB = b, фокусы такого эллипса лежат на оси Oy, причём a² = b² – c².

В случае, когда a = b, уравнение (1) принимает вид

= 1 или x² + y² = a²

и определяет окружность радиуса а с центром в начале координат (рис.4.3). В этом случае c = 0, поэтому ε = 0.

Из школьного курса известно уравнение окружности радиуса R с центром в точке A₀(x₀,y₀):

(x – x ) +(y – y ) =R .

Такое уравнение называют каноническим уравнением окружности.

Гипербола.

Определение 4.2. Гиперболой называется множество всех точек плоскости, для каждой из которых модуль разности расстояний до двух данных точек, называемыхфокусами, есть величина постоянная, меньшая, чем расстояние между фокусами.

Пусть F₁(-c,0) и F₂(c,0) ─ фокусы. Тогда F₁F₂ = 2c ─ фокусное расстояние (рис.4.4). Постоянную величину, о которой идёт речь в определении, обозначим 2a. Тогда по определению 2a < 2c, т.е. a < c.

Пусть M(x;y) ─ произвольная точка гиперболы. Рассуждая по аналогии с п. 4.1, можем получить уравнение

= 1, (2)

где b² = c² – a².

Уравнение (2) называют каноническим уравнением гиперболы. Гипербола с уравнением (2) изображена на рис.4.5.

Прямоугольник MNKL, стороны которого MN = LK = 2a, ML = NK = 2b, называется основным прямоугольником. Прямые MK и NL называют асимптотами гиперболы,их уравнения : y = – x и y = x, соответственно. Гипербола имеет две ветви: левую и правую. Центр симметрии гиперболы называется её центром. Оси симметрии гиперболы называются её осями. Одна ось пересекает гиперболу в двух точках (на рис.4.5 это т. A₁ и A₂), эта ось называется действительной осью гиперболы,другая ось ─ мнимой осью, она не имеет общих точек с гиперболой. Длины отрезков A₁A₂ и B₁B₂ также называют осями. Величины a и b называются полуосями гиперболы. Если a = b, то гипербола называется равносторонней,её уравнение

x² – y² = a².

Уравнение

- = 1 (3)

определяет гиперболу с действительной осью Oy (рис.4.6).

Гиперболы, определяемые уравнениями (2) и (3) в одной и той же системе координат, называются сопряжёнными. Эксцентриситет гиперболы─ это отношение фокусного расстояния к расстоянию между вершинамигиперболы (т.е. точками пересечения гиперболы с осями). Для уравнения (2)

ε = .

Так как c > a, то ε > 1. Фокальные радиусы точки M гиперболы─ это отрезки F₁M и F₂M. Их длины r₁ и r₂ для правой ветви

r₁ = εx + a, r₂ = εx – a,

для левой ветви

r₁ = -εx − a, r₂ = - εx + a.

Парабола.

Определение 4.3. Параболойназывается множество всех точек плоскости, каждая из которых находится на одинаковом расстоянии от данной точки, называемой фокусом, и данной прямой, называемой директрисой, и не проходящей через фокус.

Возьмём в прямоугольной системе координат точку F( ,0), где p > 0 и пусть она будет фокусом. Директрисой будет прямая x = - (рис.4.7). Пусть M(x,y) ─ произвольная точка параболы. Если K ─ основание перпендикуляра из точки M к директрисе, то она имеет координаты (- ,y). По определению 4.3

MK = MF.

Тогда

= , = , т.к. x ≥ 0.

Возводим уравнение а квадрат и приводим подобные члены:

,

y² = 2px (4)

Уравнение (4) называется каноническим уравнением параболы. Величину p называют параметром параболы. Парабола с уравнением (4) изображена на рис.4.8. Точка O называется вершиной параболы,ось симметрии ─ осью параболы. Если парабола имеет уравнение y² = - 2px, то её график расположен слева от оси Oy (рис.4.9). Уравнения x² = 2pyи x² = -2py, p > 0 определяют параболы, изображённые на рис.4.10 и рис.4.11, соответственно.

Понятие о матрице.

Таблица чисел а_ik вида

, (1)

состоящая из m строк и n столбцов называется матрицей размера m × n. Числа а_ik называются её элементами. Если m ¹ n, то матрица называется прямоугольной.Если же

m = n, то матрица называется квадратной.В частности, если m = 1, n > 1, то матрица

(а₁₁ а₁₂ … а_1n) называется матрицей-строкой. Если же m > 1, n = 1, то матрица называется матрицей-столбцом.

Число строк в квадратной матрице называют порядком такой матрицы. Например, матрица есть квадратная матрица второго порядка, а матрица есть квадратная матрица третьего порядка.

Матрицы будем обозначать большими латинскими буквами. Две матрицы A и B называются равными (А = В), если они одинакового размера и их соответствующие элементы равны. Так, если А = , В = и а₁₁ = b₁₁, a₁₂ = b₁₂, a₂₁ = b₂₁, a₂₂ = b₂₂, то А = В.

Умножение матрицы на число.

Определение. Произведением матрицы А на число αназывается матрица αА, элементы которой равны произведению числа α на соответствующие элементы матрицы А.

Умножение матриц.

Определение. Произведениемматрицы А размерности m × n и матрицы В размерности n × k, элементы которой с_ij вычисляются как сумма произведений соответствующих элементов а_il I – й строки матрицы А и элементов b_lj j – го столбца матрицы В, т.е.

c_ij = a_i1b_1j + a_i2b_2j + … + a_inb_nj, I = 1,2, …, m; j = 1,2, …, k.

Определение.Квадратная матрица порядка n вида называется единичной матрицей и обозначается E_n.

Свойства умножения матриц

1) Умножение матриц некоммутативно, т.е. AB ¹ BA.

2) Умножение матриц ассоциативно, т.е. A(BC) = (AB)C, если такие произведения существуют.

3) Если A ─ матрица размера m×n, B ─ матрица размера n×k, то A×E_n=A, E_n×B=B.

Транспонирование матрицы.

Определение.Если в матрице

А =

сделать все строки столбцами с тем же номером, то получим матрицу

А^t =

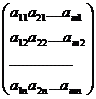
которую называют транспонированнойк матрице А.

Свойства транспонирования матриц.

1) (A^t)^t = A; 2) (A + B)^t = A^t + B^t; 3) (AB)^t = B^tA^t 4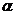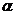)( A) ^t = A^t

5.6. Элементарные преобразования строк матрицы.

Определение. Элементарными преобразованиями строк матрицыназывают следующие преобразования:

1) умножение строки матрицы на ненулевое действительное число;

2) прибавление к одной строке матрицы другой её строки, умноженной на произвольное действительное число.

Лемма 5.1.С помощью элементарных преобразований строк матрицы можно поменять местами любые две строки.

Доказательство.

А= . .

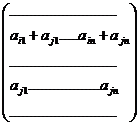
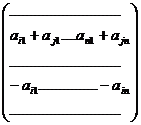
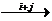
Свойства определителей.

Определение. Матрицу вида

или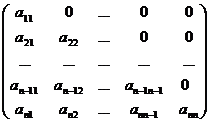

будем называть треугольной матрицей.

Свойство 1. Определитель треугольной матрицы равен произведению элементов главной диагонали, т.е.

= = .

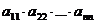Свойство 2. Определитель матрицы с нулевой строкой или нулевым столбцом равен нулю.

Свойство 3.При транспонировании матрицы определитель не изменяется, т.е.

│А│= │А^t│.

Свойство 4.Если матрица В получается из матрицы А умножением каждого элемента некоторой строки на число k, то

│В│= k│А│.

Свойство 5.

= + .

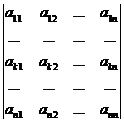Свойство 6.Если матрица В получается из матрицы А перестановкой двух строк,

то│В│= −│А│.

Свойство 7.Определитель матрицы с пропорциональными строками равен нулю, в частности, нулю равен определитель матрицы с двумя одинаковыми строками.

Свойство 8.Определитель матрицы не изменяется, если к элементам одной строки прибавить элементы другой строки матрицы, умноженные на некоторое число.

Замечание. Так как по свойству 3 определитель матрицы не меняется при транспонировании, то все свойства о строках матрицы верны и для столбцов.

Свойство 9.Если А и В ─ квадратные матрицы порядка n, то │АВ│=│А││В│.

Обратная матрица.

Определение.Квадратная матрица А порядка n называется обратимой,если существует матрица В такая, что АВ = ВА = Е_n. В этом случае матрица В называется обратной к матрицеА и обозначается А^-1.

Теорема 2.Справедливы следующие утверждения:

1) если матрица А обратима, то существует точно одна ей обратная матрица;

2) обратимая матрица имеет определитель, отличный от нуля;

3) если А и В ─ обратимые матрицы порядка n, то матрица АВ обратима, причём (АВ)^-1 =

= В^-1 ×А^-1.

Доказательство.

1) Пусть В и С ─ матрицы, обратные к матрице А, т.е. АВ = ВА = Е_n и АС = СА = Е_n. Тогда В = ВЕ_n = В(АС) = (ВА)С = Е_nС = С.

2) Пусть матрица А обратима. Тогда существует матрица А^-1, ей обратная, причём

АА^-1 = Е_n.

По свойству 9 определителя │АА^-1│=│А││А^-1│. Тогда │А││А^-1│=│Е_n│, откуда

│А││А^-1│= 1.

Следовательно, │А│¹ 0.

3) Действительно,

(АВ)(В^-1А^-1) = (А(ВВ^-1))А^-1 = (АЕ_n)А^-1 = АА^-1 = Е_n.

(В^-1А^-1)(АВ) = (В^-1(А^-1А))В = (В^-1Е_n)В = В^-1В = Е_n.

Следовательно, АВ ─обратимая матрица, причём (АВ)^-1 = В^-1А^-1.

Следующая теорема даёт критерий существования обратной матрицы и способ её вычисления.

Теорема 3. Квадратная матрица А обратима тогда и только тогда, когда её определитель отличен от нуля. Если │А│¹ 0, то

А^-1 = .

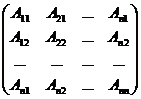Систем линейных уравнений.

Совокупность уравнений вида

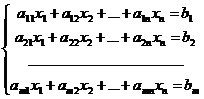(1)

называется системой m линейных уравнений с n неизвестнымих_1, х_2,…, х_n. Числа a_ij называются коэффициентами системы,а числа b_i ─ свободными членами.

Решением системы (1)называется совокупность чисел с₁, с₂,…, с_n, при подстановке которых в систему (1) вместо х₁, х₂,…,х_n, получаем верные числовые равенства.

Решить систему ─ значит найти все её решения или доказать, что их нет. Система называется совместной, если она имеет хотя бы одно решение, и несовместной, если решений нет.

Матрица, составленная из коэффициентов системы

А =

Называется матрицей системы (1). Если к матрице системы добавить столбец свободных членов, то получим матрицу

В = ,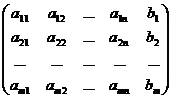

которую называют расширенной матрицей системы (1).

Если обозначим

Х = , С = , то систему (1) можно записать в виде матричного уравнения АХ=С.

Теорема Кронекера-Капелли.

Для того, чтобы система линейных уравнений была совместна, необходимо и достаточно, чтобы ранг матрицы системы был равен рангу расширенной матрицы.

Понятие вектора.

Некоторые физические величины (например: температура, масса, объём, длина) могут быть охарактеризованы одним числом, которое выражает отношение этой величины к соответствующей единицы измерения. Такие величины называются скалярными. Другие величины (например: сила, скорость, ускорение) характеризуются не только числом, но и направлением. Эти величины называются векторными. Для описания таких величин в математике введено понятие «вектор».

Определение. Любая упорядоченная пара точек А и В пространства определяет направленный отрезок, т.е. отрезок с заданными на нём направлением. Направленный отрезок называется вектором. На рисунке направление вектора обычно изображают стрелкой. Если в упорядоченной паре точка А первая, то её называют началом вектором, а точку В ─ концом вектора,в этом случае вектор обозначается . Иногда векторы обозначают малыми буквами 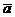, 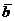и т.д.

Модулем вектора 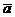называется его длина. Обозначают модуль или 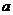. Нуль-вектор (или нулевой вектор) ─ это вектор, начало и конец которого совпадают; обозначается он 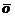. Модуль нуль-вектора равен нулю, а направление не определено. Единичнымназывается вектор, длина которого равна единице.

Векторы 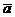и 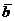называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.

Коллинеарные векторы могут быть направлены одинаково или противоположно (рис.8.2).

Векторы 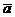и 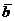называются равными(обозначается 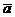= 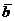), если они коллинеарны, одинаково направлены и имеют равные модули.

Векторы 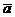и 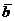называются противоположными(обозначается 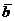= − 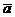), если они коллинеарны, противоположно направлены и имеют равные модули.

Три вектора 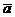, , 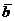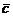называются компланарными,если они лежат в одной плоскости.

Проекция вектора на ось.

Пусть в пространстве задана ось ℓ и некоторый вектор (рис.8.7). Пусть А₁ ─ проекция точки А на ось ℓ, В₁ ─ проекция точки В на ось ℓ.

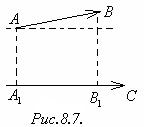Проекцией вектора на ось ℓ называется величина А₁В₁ вектора 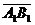, взятая со знаком «+», если 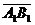совпадает с направлением оси ℓ, и со знаком «−», если 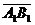противоположно направлен направлению оси ℓ. Обозначается: пр_ℓ .

Координаты вектора.

Пусть в пространстве заданы прямоугольная система координат Oxyz и произв­ольный вектор . Пусть Х = пр_х , У = пр_х , Z = пр_х . Проекции X, Y, Z вектора на оси координат называют его координатами. При этом пишут = (Х, У, Z).

Теорема 8.1.Для любых точек А(х₁;у₁;z₁) и В(х₂;у₂;z₂) координаты вектора , определяются формулы:

Х = х₂ – х₁, У = у₂ – у₁, Z = z₂ – z₁.

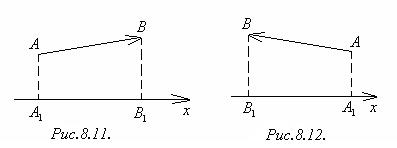
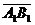Доказательство. По определению Х = пр_х . Если вектор направлен одинаково с осью Ох (рис.8.11), то пр_х А(х₁;у₁;z₁) и В(х₂;у₂;z₂) = │ 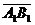│= = 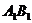х₂ – х₁, т.к. точке А₁ соответствует координата х₁, а точка В ─ координата х₂.

Если вектор 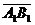направлен противоположно с осью Ох (рис.8.12), то

пр_х = −│ │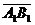= − = −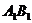(х₁ – х₂) = х₂ – х₁.

Таким образом, для любых точек А(х₁;у₁;z₁) и В(х₂;у₂;z₂) координата Х вектора вычисляется по формуле Х = х₂ – х₁.

Аналогично доказывается остальные формулы.

Пусть 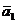=(х₁;у₁;z₁), 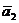=(х₂;у₂;z₂),…, 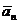=(х_n;у_n;z_n) ─ векторы пространства, 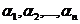─ ненулевые числа. Используя свойства проекции векторов на ось, получим следующие утверждения:

1) = ( ).

2) 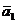+ + 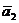… + 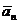=(х₁ +…+ х_n; y₁ +…+ у_n; z₁ + …+ z_n).

3) 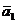− 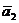=(х₁ – х₂; у₁ – у₂; z₁ – z₂).

4) +... + = ( ).

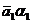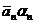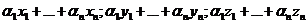5) 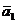= 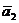Þх₁ = х₂, у₁ = у₂, z₁ = z₂.

Доказательство.

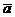
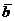
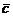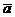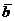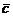= ( × )× = х₃ × 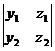− у₃ × 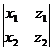+ z₃ × = .

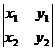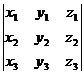Определение. Уравнением поверхностив заданной системе координат в пространстве называется такое уравнение с тремя переменными, которому удовлетворяют координаты любой точки данной поверхности и только они.

Поверхность, определяемая алгебраическим уравнением n-й степени относительно декартовых координат, называется поверхностью n-го порядка. Мы рассмотрим поверхности 1-го и 2-го порядков.

Плоскость в пространстве.

Общее уравнение плоскости.

Раскроем скобки в уравнении (1):

А(х - х₀) + В(у - у₀) + С(z - z₀) = 0

Ах + Ву +Сz + (- Ах₀ – Ву₀ – Сz₀) = 0

Обозначим через D = - Ах₀ – Ву₀ – Сz₀ . Получаем уравнение

Ах + Ву +Сz + D = 0, (2)

которое называется общим уравнением плоскости.

Частные случаи:

1) D = 0. Уравнение Ах + Ву +Сz = 0 определяет плоскость, проходящую через начало координат.

2) С = 0. В этом случае нормальный вектор 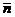(А;В;0) перпендикулярен оси Оz. Поэтому плоскость Ах + Ву + D = 0 параллельна оси Оz.

3) С = 0, D = 0. С учётом п.1) и п.2) плоскость Ах +Ву = 0 проходит через ось Oz.

4) В = 0, С = 0. В этом случае нормальный вектор 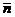(А;0;0) перпендикулярен плоскости Oyz. Поэтому плоскость Ах + D = 0 параллельно оси Oyz.

5) В = 0, С = 0, D = 0. Плоскость Ах = 0 или х = 0 определяет координатную плоскость Oyz.

Аналогично рассматриваются всевозможные другие случаи.

Прямая в пространстве.

Угол между двумя прямыми.

Рассмотрим две прямые с направляющими векторами 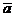= (а₁;а₂;а₃) и .

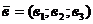Угол между прямыми равен углу между их направляющими векторами, поэтому

cosj = 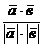= 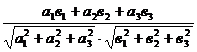(7)

Условие перпендикулярности прямых:

а₁в₁ + а₂в₂ + а₃в₃ = 0.

Условие параллельности прямых:

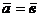l,

т.е.

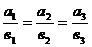. (8)

Цилиндры второго порядка.

О