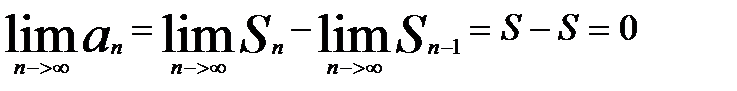Понятие линейной независимости ф-й. Опр-ль Вронского

Совок-ть ф-й 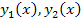наз-ся лин-завис. на промеж. (a,b), если такие числа 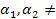одноврем.0, что 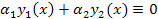, в противном усл. ф-и 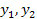наз. лин-независ.

Опр-ль Вронского

W(x)= = )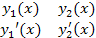

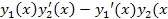Теорема. Если сист. ф-й 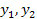лин-незав. на пром.(a,b),то их опр-ль Вронского 0 на (a.b)

Следствие(дост.усл.лин.незав.ф-й). Если опр-ль Вронского отличен от 0 хотя бы в одной точке из пром(a,b), то сист. ф-й лин. незав на (a,b)

Линейные однородные ДУ 2 порядка с постоянными коэфф-ми. Их нахождение. Общее решение.

Обыкн ДУ 2 порядка с пост.коэфф. имеет вид:

(1) y``+py`+qy=r(x) p,q принадл. R, r(x) – функция

Если r(x) =0, то

(2) y``+ py`+qy=0 – однор.лин.ДУ с пост.коэфф.

Ур-е вида (3) 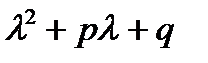=0 – характерист.ур-е (1) и(2) Стр-ра общего решения ур.(2) определяется корнями квадр.ур-я. (3)

Возможны 3 случая

1. кв.ур-е имеет разные корни α1 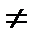α2, D>0 тогда общее решение:

y=C1 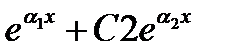C1, C2 прин.R

2. корни кв.ур. кратные, т.е. α1= α2=α ; D=0

y= 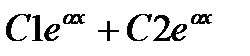C1, C2 прин.R

3. корни комплексно сопряженные : λ1= α-βi; λ2= α+βi;

y= C1 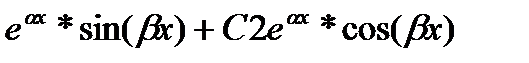C1, C2 прин.R

Лин неоднор ДУ 2-го порядка с пост коэфф-ми.

Рассмотрим уравнение y´´+py´+qy=r(x) /где p,q ? R , r(x)-функция. которое имеет вид y=yO+yЧ, где

yO-общее решение уравнения y´´+py´+qy =0

yЧ-частное решение уравнения y´´+py´+qy=r(x) , которое зависит от вида правой части,т.е r(x)

Рассмотрим некоторые частные случаи:

1) r(x)=Pn(x) ,где Pn(x) – многочлен степени «n»

В этом случае решение yЧ ищут из уравнения к²+pк+q=0 в виде:

• yЧ=Qn(x) при q≠0

• yЧ=x Qn(x) q=0, p≠0

• yЧ=x² Qn(x) q=p=0

Приложения ДУ к реш-ю физ. и эк. задач

Демографическая модель

Из статистики известно, что для конкр региона число рожд и умерш за ед врем проп-но числ-ти населения с коэф. Проп-ти k₁,k₂. Найти закон измен числ-ти населения с течением времени, т.е. опис матем демограф процесс.

Реш. Пусть y=y(t) –число жителей региона в момент времени t.

∆у – прирост населения за время ∆t

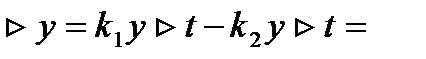
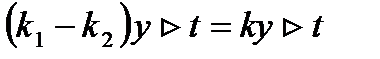где k=k₁-k₂

Разделим на ∆t

,

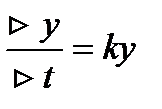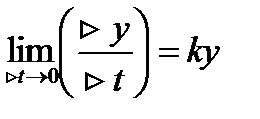
y’=ky, где k=k1-k2 y=ce^kx

67.Св-ва степенных рядов:

1. сума степен. ряда - есть ф-ия непрерыв. на любом отрезке, содержащимся внутри интервала сходимости

2. степен. ряд можно почленно интегрир. на любом отрезке, содерж. в интервале. Получ. ряд будит иметь такой же радиус сходимости как и исходный.

3. степен. ряд можно почленно дифф-ть любое число раз, радиус сход. его при это не изменится

Числовой ряд и его сумма. Свойства сходящихся рядов.

Числовым рядомназыв. выражение вида а1+а2+…+аn+…, кот. можно записать 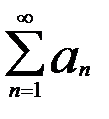(1)

а1, а2 – члены ярда

аn – общий член ряда или n-ый член ряда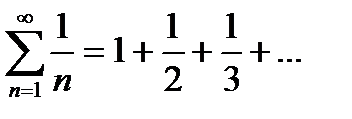

Сумма n-первых членов ряда Sn=a1+a2+..+an назыв. n-ой частичной суммой ряда.

Числовой ряд назыв. сходящимся,если сущ. конечн. предел последоват. Sn=S, S принадлеж. R, S - сумма ряда.

Св-ва сход. рядов:

1.сходимость ряда не нарушается, если произвольным образом изменить (добавить, отбросить) конечное число членов ряда

2. сход. ряда можно почленно умножить на любое число, т.е. общий член множителей можно вынести за знак скобку ,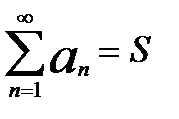

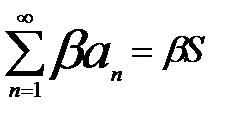
3. сход. ряды можно почленно складывать и отнимать

, ,

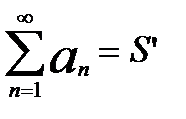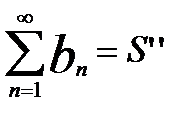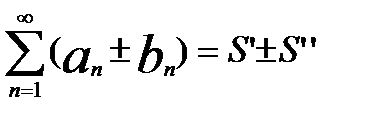
Необходимое условие сходимости числового ряда.

Если ряд 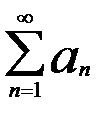- сход., то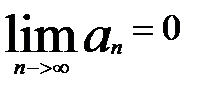

Док-во:

, ,
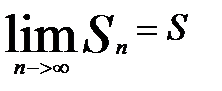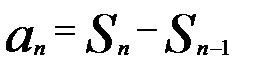