Непосредственное интегрирование.

Это вычисл. интегр. с использ. осн. св-в неопр. интегр. и списка табл. интегр.Данный метод также примен. и после предварит. преобр. подынтегрального выр-я к табл.форме.

10.Интегрир-е путем замены переменной (подстановкой)

М-д подстановки

∫f(x)dx= [x=φ(t),t=ψ(x),dx=φ’(t)dt] =∫f(φ(t)φ’(t)dt

Если интеграл непосредственно не вычисляется,можно применить метод,кот. состоит в след.:

-вводится новая переменная

x=φ(t),где t=ψ(x) явл. обратной по отношению к φ(t), dx=φ’(t)dt- дифференциал ф-ции x=φ(t)

Если подстановка выбрана удачно, то интеграл, получ в правой части, вычисляется проще, чем в исходной.

Если ф-ция x=φ(t) непрерывна и монотонна,то обратн. t=ψ(x) всегда сущ.

Вычислив интеграл в правой части по t,следует вернуться к переменной x

∫f(ψ(x)) φ’(x)dx=∫f(t)dt, где t=ψ(x)

1 ∫f(ax+b)dx= ax+b=t, x=(t-b)/a

dx=1/a dt

=∫f(t)1/a dt=1/a ∫f(t)dt=1/a F(t)+C=

=1/a F(ax+b)+C

2 ∫ f’(x)/f(x) dx= ln f(x) +C

3 ∫ df(x)/f(x) = ln f(x) +C

Метод интегрирования по частям

Задано: U=U(x), V=V(x),известно: d(UV)=VdU+UdV

проинтегрируем обе части уравнения:

∫ d(UV)= ∫ VdU+ ∫ UdV

UV=∫ VdU+ ∫ UdV=> ∫UdV=UV-∫VdU- ф-ла интегр-я по частям

Смысл ф-лы интегр-я по частям сост в след.: подинтегр выраж-е UdV разб-ся на 2 части т. о.,чтобы интеграл в правой части вычислялся проще,чем исходный.

Основные классы ф-ций,интегрируемых по частям:

1 ∫ ln^m(x)dx, ∫arcsin^mxdx, ∫arccos^m xdx,∫arctg^m xdx

2 ∫Pn(x)lnaxdx,∫Pn(x)e^axdx,∫ Pn(x)sinaxdx,

∫Pn(x)cosaxdx

3 ∫e^axsinbxdx,∫e^axbxdx

4 ∫ (x²+a²)½dx, ∫(a²- x²)½dx, ∫ dx/(x²+a²)^k

Интегрирование выражений, сод-х квадратный трехчлен

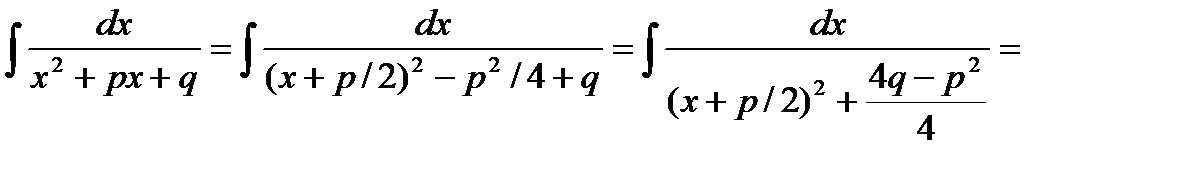x+p/2=t dx=dt a²=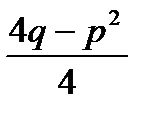 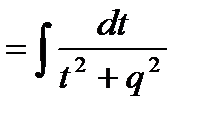или

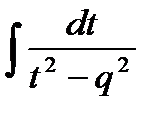
IV

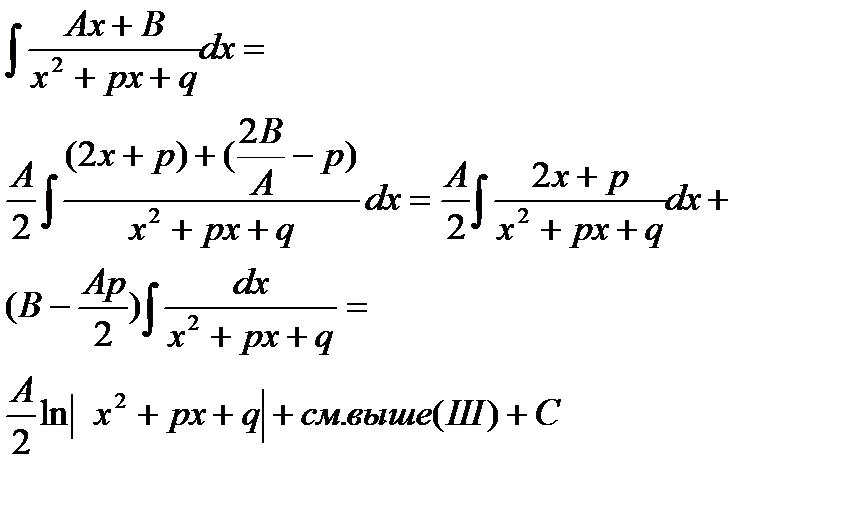
V. 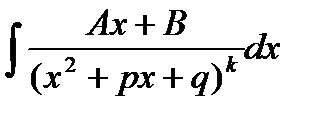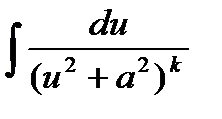p²/4-q>0

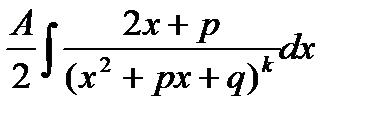p²/4-q<0

Интегрирование рациональных дробей

1. Многочленом степени n наз-ся выражение вида a₀+a₁x+a₂x²+…+a_nxⁿ=P_n(x)

Рациональной дробью наз-ют отношение двух многочленов вида 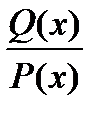При n=0 вычисление интеграла никаких трудностей не представляет

Интерес представляют рациональные дроби, у кот. n>0 При этом будем рассматривать дроби, у кот. m<n Если m>=n, то применяют процедуру деления многочленов уголком

Интегрирование простейших дробей

I. 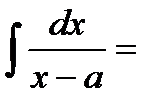x-a=t dx=dt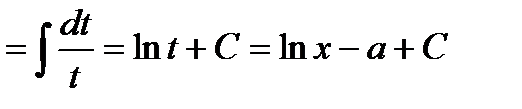

II. 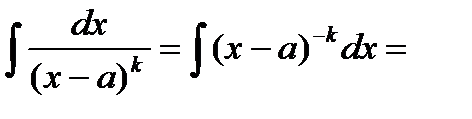x-a=t dx=dt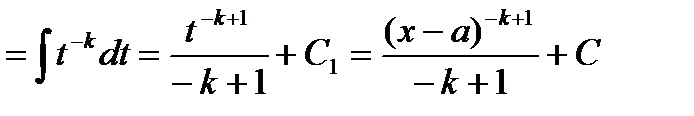

Интегрирование спец. классов ф-й .

Для нахожд. интегр. вида 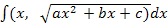примен. подстановки Эйлера:

1) 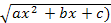= ±x 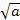+t,если а>0

2) 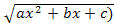= ± 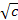+xt, если с>0

3) Если 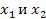– действ. корни трёхчлена 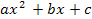, то в этом случа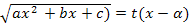е , где 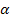– один из корней 3хчлена.

Замена переменной в определенном интеграле.

Пусть 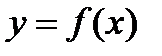непрерывна н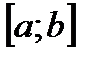а , а 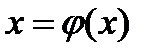непрерывна на 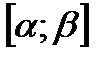. Вместе со своей производной 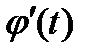; причем 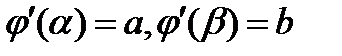, и сложная функция 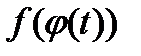непрерывна на 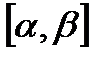, тогда справедливо формула замены переменной для определенного интеграла: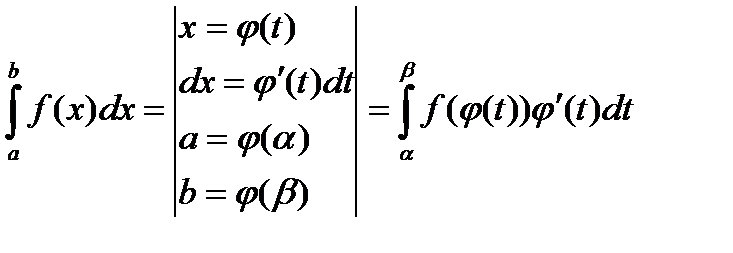

Интегрирование по частям в О.И.

Пусть заданны 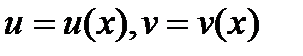тогда имеет место интегрирование по частям:

→

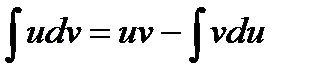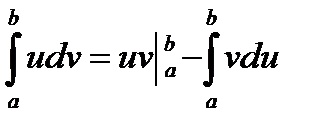
Формула Ньютона-Лейбница.

Если ф-ция f(х) непрерывна на [a,b] и ф-я F(x) какая-либо первообразная для f(x) на отрезке[a,b] то справедлива формула

.

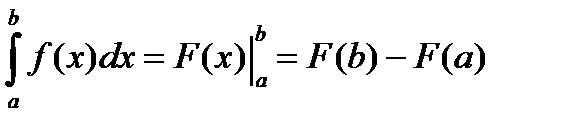Док-во:

пусть F(x)первообразная для f(x) на отрезке [a,b], ф-ция Ф(х) так же явл.первообразной. по теореме о множестве первообразных имеем Ф(х)-F(x)=C. Подставим в последнее рав-во вместо х сначала а, потом b=х получим:

Ф(а)-F(a)=C Ф(b)-F(b)=C Ф(а)=∫_a^a f(x)dx=0 Ф(b)=∫_a^b f(x)dx

Имеем C=-F(a) ∫_a^b f(x)dx+F(a)=F(b) ∫_a^b f(x)dx=F(b)-F(a)

17.Опред. интеграл в эк-ке:

u=f(t) – пр-ть труда, тогда V прод-ии, произвед. за время от t до t2 равен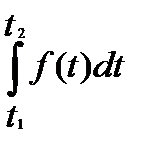

Пусть ф-ия k(x) опред. зависим. TC от Q прод-ии x, тогда f знач. TC при выпуске Q от а до b, x принадлеж. [a; b], опред.: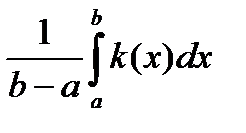

Частные пр-е 1го порядка

Рассм ф-ю 2 перем. z=f(x,y), где x,y 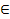Ω с 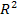.Возьмём любую точку 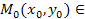Ω, через ∆x и ∆y обозначим приращение по х и у, тогда полное приращение имеет вид:∆z=f( 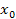+∆x, 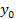+∆y)-f( 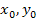). Рассм. отн-е частного прир-я по пер-й z к вызвавшему его прир-ю: рассм. предел, когда ∆x→0, этот предел может существовать и не сущ-ть. Если сущ-т, то он наз. 1й част. пр-й по пер-й х ( 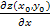, z`x):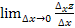

Для того, чтобы находить 1й част. пр-е примен. след правило: 1я част. пр-я по х – это обыкн. пр-я по пер-й х при усл., что у=const