Решение линейной краевой задачи методом пристрелки
СОДЕРЖАНИЕ
1. ВВОДНАЯ РАБОТА ПО ОВЛАДЕНИЮ НАВЫКАМИ РАБОТЫ В ПАКЕТЕ MATHCAD 3
2. Решение задачи Коши.. 6
ВАРИАНТЫ ЗАДАНИЙ.. 7
3. РЕШЕНИЕ КРАЕВОЙ ЗАДАЧИ.. 9
ВАРИАНТЫ ЗАДАЧ.. 10
3. ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ.. 13
ВАРИАНТЫ ЗАДАНИЙ И ОТВЕТЫ... 14
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ.. 20
Решение дифференциальных уравнений.. 20
Решение задачи Коши.. 20
Метод Эйлера. 20
Модифицированные методаы Эйлера. 20
Метод Рунге–Кутта. 21
Оценка погрешности решения по правилу Рунге. 21
Метод Рунге-Кутта-Фельберга. 21
Метод Предиктор-Корректор с использованием метода Адамса. 22
Краевая задача для обыкновенных дифференциальных уравнений.. 23
Решение линейной краевой задачи методом редукции к задачам Коши.. 23
Решение линейной краевой задачи методом конечных разностей.. 24
Решение краевой задачи методом пристрелки.. 25
Вычисление интегралв. 27
Квадратурные формулы Гаусса и Ньютона-Котеса. 27
1. ВВОДНАЯ РАБОТА ПО ОВЛАДЕНИЮ НАВЫКАМИ РАБОТЫ В ПАКЕТЕ MATHCAD
Задание: В среде Mathcad полностью напечатать приведенный ниже текст, запустить на счет и разобраться в полученных результатах.
Для получения зачета нужно уметь объяснить, как выполняется каждая команда. Описание команд содержится в Краткой инструкции пользователя пакета прикладных программ Mathcad.
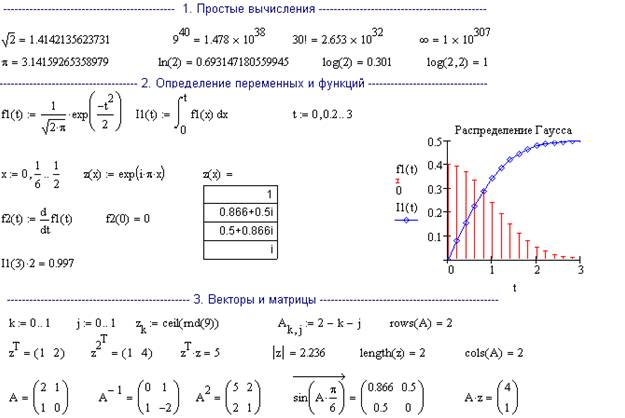
Заголовок работы: “Лабораторная работа студента группы №, Ф. И.”.
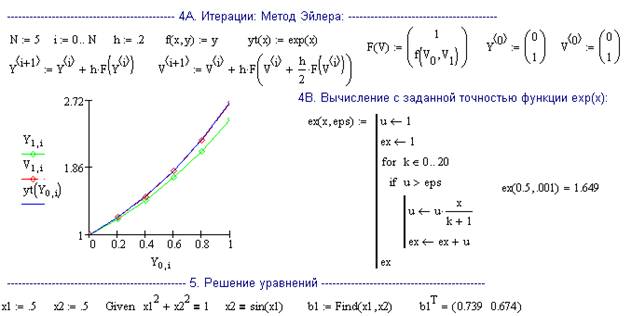
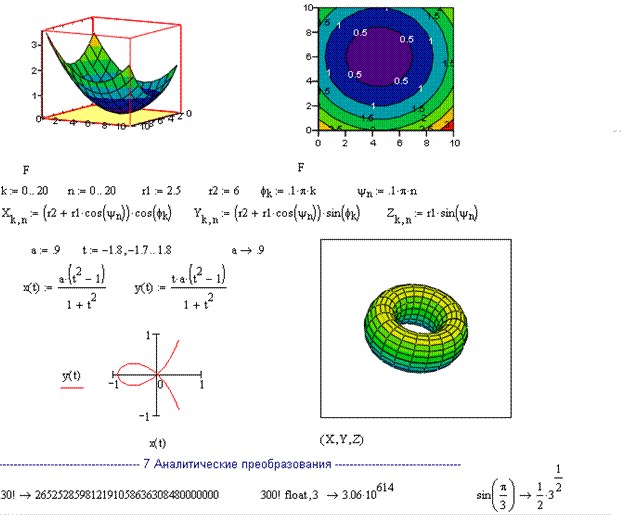
2. Решение задачи Коши
Каждый студент получает свое задание на одну из двух тем. Студент должен создать программу решения на языке Mathcad и провести расчеты.
Для получения зачета студент должен продемонстрировать на экране компьютера действующую программу, реализующую решение поставленных задач. Студент должен уметь объяснить все детали представленной программы и ответить на связанные с темой теоретические вопросы.
1. Решение задачи Коши методом Рунге‑Кутта‑Фельберга
Найти решение дифференциального уравнения на отрезке [a,b] с заданной точностью с автоматическим выбором шага приращения аргумента. Построить совмещенный график приближенного и точного решения. Построить совмещенный график оценки погрешности и истинной погрешности решения. Проверить, как меняется решение при изменении заданной точности и при увеличении длины отрезка изменения аргумента.
2. Решение задачи Коши методом Предиктор-Корректор
Найти решение дифференциального уравнения на отрезке [a,b] с заданным значением шага приращения аргумента h = (b-a)/n. В методе Предиктор-Корректор использовать формулы Адамса четвертого порядка. Для нахождения первых трех значений неизвестной функции использовать метод Рунге-Кутта четвертого порядка. Построить совмещенный график приближенного и точного решения. Построить совмещенный график оценки погрешности и истинной погрешности решения. Проверить, как меняется погрешность при изменении шага приращения аргумента и при увеличении длины отрезка изменения аргумента.
ВАРИАНТЫ ЗАДАНИЙ
- Решить задачу Коши методом Рунге-Кутта-Фельберга
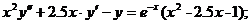
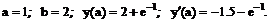
Точное решение: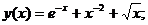 
- Решить задачу Коши методом Предиктор-Корректор
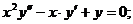
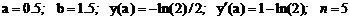
Точное решение: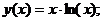 
- Решить задачу Коши методом Рунге-Кутта-Фельберга
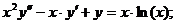
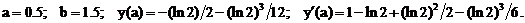
Точное решение: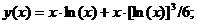 
- Решить задачу Коши методом Предиктор-Корректор
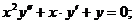
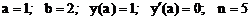
Точное решение: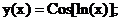 
- Решить задачу Коши методом Рунге-Кутта-Фельберга
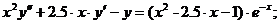
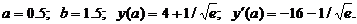
Точное решение: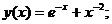 
- Решить задачу Коши методом Предиктор-Корректор:
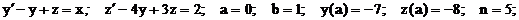
Точное решение: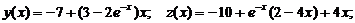 
- Решить задачу Коши методом Рунге-Кутта-Фельберга
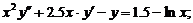
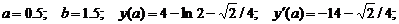
Точное решение: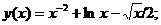 
- Решить задачу Коши методом Предиктор-Корректор:
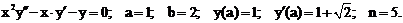
Точное решение: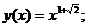 
- Решить задачу Коши методом Рунге-Кутта-Фельберга
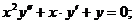
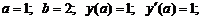
Точное решение: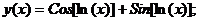 
- Решить задачу Коши методом Предиктор-Корректор:
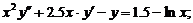
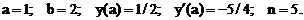
Точное решение: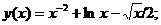
- Решить задачу Коши методом Рунге-Кутта-Фельберга
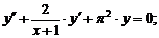
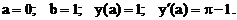
Точное решение: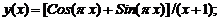 
- Решить задачу Коши методом Предиктор-Корректор:
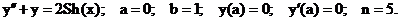
Точное решение: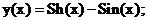 
- Решить задачу Коши методом Рунге-Кутта-Фельберга
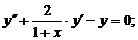
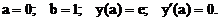
Точное решение: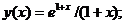 
- Решить задачу Коши методом Предиктор-Корректор:
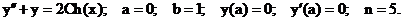
Точное решение: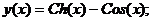 
- Решить задачу Коши методом Рунге-Кутта-Фельберга
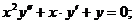
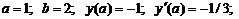
Точное решение: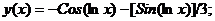 
- Решить задачу Коши методом Предиктор-Корректор:
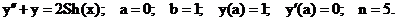
Точное решение: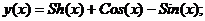 
- Решить задачу Коши методом Рунге-Кутта-Фельберга
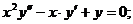
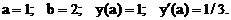
Точное решение: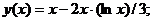 
- Решить задачу Коши методом Предиктор-Корректор:
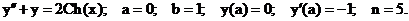
Точное решение: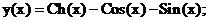 
- Решить задачу Коши методом Рунге-Кутта-Фельберга
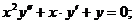
Точное решение: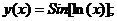 
- Решить задачу Коши методом Предиктор-Корректор:
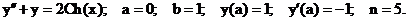
Точное решение: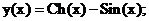 
- Решить задачу Коши методом Рунге-Кутта-Фельберга
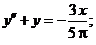
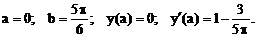
Точное решение: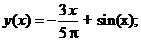 
- Решить задачу Коши методом Предиктор-Корректор:
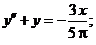
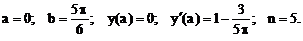
Точное решение: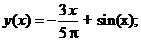
- Решить задачу Коши методом Рунге-Кутта-Фельберга
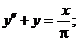
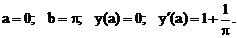
Точное решение: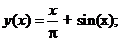 
- Решить задачу Коши методом Предиктор-Корректор:
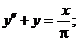
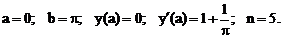
Точное решение: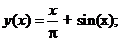
РЕШЕНИЕ КРАЕВОЙ ЗАДАЧИ
Каждый студент получает свое задание на одну из трех тем. Студент должен создать программу решения на языке Mathcad и провести расчеты.
Для получения зачета студент должен продемонстрировать на экране компьютера действующую программу, реализующую решение поставленных задач. Студент должен уметь объяснить все детали представленной программы и ответить на связанные с темой теоретические вопросы.
1. Решение линейной краевой задачи методом редукции к задачам Коши
Найти решение дифференциального уравнения на отрезке [a,b] с заданным значением шага приращения аргумента h = (b-a)/n. Для решения возникающих задач Коши использовать метод Рунге–Кутта четвертого порядка. Построить совмещенный график точного и приближенного решений. Построить график погрешности решения. Проверить, как меняется погрешность при изменении шага приращения аргумента.
2. Решение линейной краевой задачи методом конечных разностей
Найти решение дифференциального уравнения на отрезке [a,b] с заданным (h = (b-a)/n) и с половинным (h/2) значением шага приращения аргумента. Построить совмещенные графики решений с шагом h и с шагом h/2, точного решения и решения, уточненного по правилу Рунге. Построить совмещенные графики оценки погрешности и истинной погрешности для решений с шагом h и h/2, и уточненного решения. Проверить, как меняется погрешность при изменении шага приращения аргумента.
ВАРИАНТЫ ЗАДАЧ
- Решить линейную краевую задачу методом редукции к задачам Коши
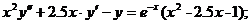
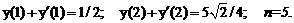
Точное решение: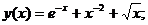
- Решить линейную краевую задачу методом конечных разностей
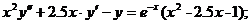
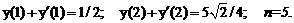
Точное решение: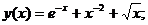
- Решить линейную краевую задачу методом пристрелки
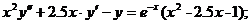
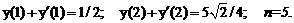
Точное решение: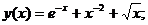
- Решить линейную краевую задачу методом редукции к задачам Коши
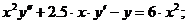
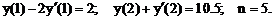
Точное решение: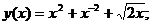 
- Решить линейную краевую задачу методом конечных разностей:
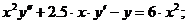
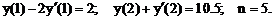
Точное решение: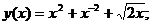
- Решить линейную краевую задачу методом пристрелки:
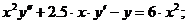
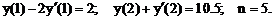
Точное решение: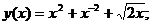
- Решить линейную краевую задачу методом редукции к задачам Коши
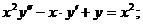
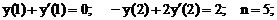
Точное решение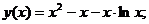 
- Решить линейную краевую задачу методом конечных разностей:
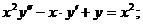
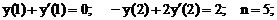
Точное решение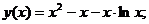
- Решить линейную краевую задачу методом пристрелки:
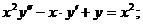
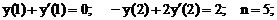
Точное решение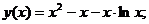
- Решить линейную краевую задачу методом редукции к задачам Коши
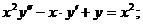
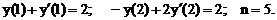
Точное решение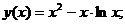 
- Решить линейную краевую задачу методом конечных разностей:
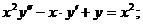
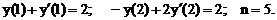
Точное решение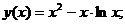
- Решить линейную краевую задачу методом пристрелки:
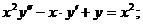
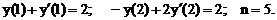
Точное решение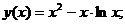
- Решить линейную краевую задачу методом редукции к задачам Коши
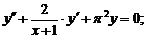
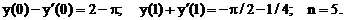
Точное решение: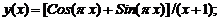
- Решить линейную краевую задачу методом конечных разностей:
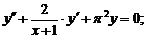
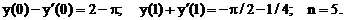
Точное решение: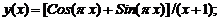
- Решить линейную краевую задачу методом пристрелки:
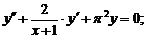
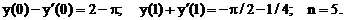
Точное решение: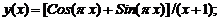
- Решить линейную краевую задачу методом редукции к задачам Коши
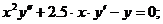
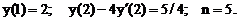
Точное решение: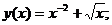 
- Решить линейную краевую задачу методом конечных разностей:
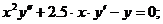
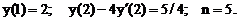
Точное решение: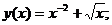
- Решить линейную краевую задачу методом пристрелки:
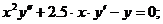
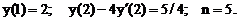
Точное решение: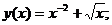
- Решить линейную краевую задачу методом редукции к задачам Коши
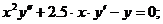
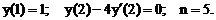
Точное решение: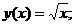 
- Решить линейную краевую задачу методом конечных разностей:
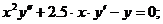
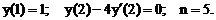
Точное решение: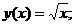
- Решить линейную краевую задачу методом пристрелки:
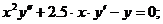
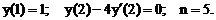
Точное решение: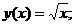
- Решить линейную краевую задачу методом редукции к задачам Коши
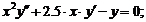
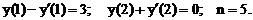
Точное решение: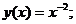 
- Решить линейную краевую задачу методом конечных разностей:
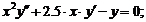
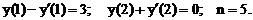
Точное решение: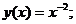
- Решить линейную краевую задачу методом пристрелки:
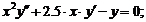
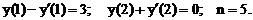
Точное решение: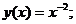
- Решить линейную краевую задачу методом редукции к задачам Коши
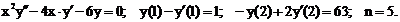
Точное решение: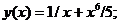 
- Решить линейную краевую задачу методом конечных разностей:
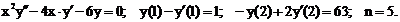
Точное решение: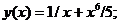
- Решить линейную краевую задачу методом пристрелки:
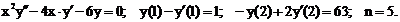
Точное решение: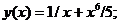
- Решить линейную краевую задачу методом редукции к задачам Коши
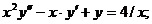
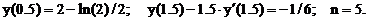
Точное решение: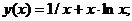 
- Решить линейную краевую задачу методом конечных разностей:
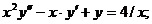
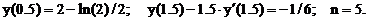
Точное решение: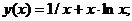
- Решить линейную краевую задачу методом пристрелки:
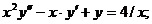
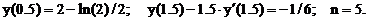
Точное решение: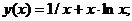
- Решить линейную краевую задачу методом редукции к задачам Коши
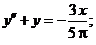
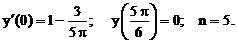
Точное решение: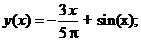
- Решить линейную краевую задачу методом конечных разностей:
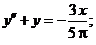
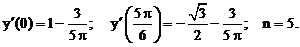
Точное решение: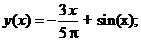
- Решить линейную краевую задачу методом пристрелки:
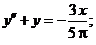
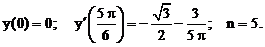
Точное решение: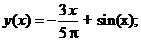
- Решить линейную краевую задачу методом редукции к задачам Коши
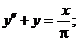
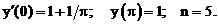
Точное решение: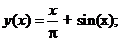
- Решить линейную краевую задачу методом конечных разностей:
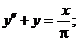
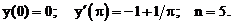
Точное решение: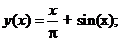
- Решить линейную краевую задачу методом пристрелки:
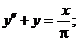
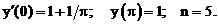
Точное решение: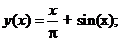
- Решить линейную краевую задачу методом редукции к задачам Коши
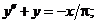
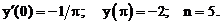
Точное решение: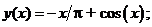 
- Решить линейную краевую задачу методом конечных разностей:
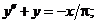
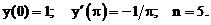
Точное решение: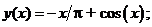
- Решить линейную краевую задачу методом пристрелки:
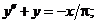
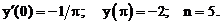
Точное решение: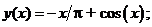
ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ
Требуется выполнить два задания.
а) Построить график изменения подинтегральной функции. Вычислить интеграл с помощью формул Гаусса и Ньютона-Котеса, предварительно выбрав весовую функцию и определив узлы интерполяции и коэффициенты интерполяционной формулы. Расчет провести для трех и четырех узлов. В случае бесконечных пределов интегрирования крайние узлы в формуле Ньютона-Котеса располагать в тех же точках, что и узлы формулы Гаусса. Для каждого из методов найти погрешность вычислений, сравнив результаты расчетов с точным значением интеграла.
б) Построить график изменения подынтегральной функции. Вычислить интеграл, используя составную формулу Симпсона, а также формулу Симпсона совместно с процессом Эйткена. Найти эффективный порядок формулы. Для каждого из методов найти погрешность вычислений. Проверить, как меняется погрешность вычислений при изменении числа подотрезков, на которые делится отрезок интегрирования.
Замечание. Программы Mathcad и Mathematica по умолчанию не раскрывают неопределенности вида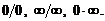 
Во избежание ошибок в точках, где имеют место неопределенности, следует в явном виде вычислять пределы.
Для получения зачета студент должен продемонстрировать на экране компьютера действующую программу, реализующую решение поставленных задач. Студент должен уметь объяснить все детали представленной программы и ответить на связанные с темой теоретические вопросы.
ВАРИАНТЫ ЗАДАНИЙ И ОТВЕТЫ
Обозначения:
ErrHauss3, ErrHauss4 – погрешность вычислений по формуле Гаусса с тремя и четырьмя узлами.
ErrNewtCot3, ErrNewtCot4 – погрешность вычислений по формуле Ньютона-Котеса с тремя и четырьмя узлами.
ErrSimps – погрешность вычислений по формуле Симпсона при разбиении отрезка интегрирования [a,b] на 4m подотрезков.
ErrAtk – погрешность вычислений по формуле Эйткена при использовании разбиений отрезка интегрирования [a,b] на m, 2 m и 4m подотрезков.
1. а)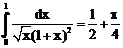 
б) 
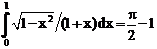
ErrHauss3=-0.000330 ErrHauss4=-0.0000125 ErrSimps=-0.000894 m=2
ErrNewtCot3=0.0220 ErrHauss4=0.00589 ErrAtk=0.0000158 p=1.48
--------------------------------------------------------------------------------------------------------------------
2. а)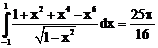 
б) 
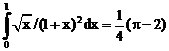
ErrHauss3=0.0982 ErrHauss4=0. ErrSimps=-0.00130 m=2
ErrNewtCot3=-0.196 ErrNewtCot4=-0.177 ErrAtk=-0.0000752 p=1.60
--------------------------------------------------------------------------------------------------------------------
3. а)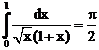 
б) 
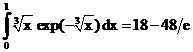
ErrHauss3=-0.0000646 ErrHauss4=-0.00000191 ErrSimps=-0.00298 m=2
ErrNewtCot3=0.00698 ErrNewtCot4=0.00158 ErrAtk=0.0000944 p=1.25
--------------------------------------------------------------------------------------------------------------------
4. а)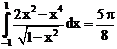 
б) 
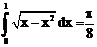
ErrHauss3=0. ErrHauss4=0. ErrSimps=-0.00255 m=2
ErrNewtCot3=-0.393 ErrNewtCot4=-0.218 ErrAtk=0.0000243 p=1.52
--------------------------------------------------------------------------------------------------------------------
5. а)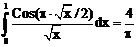 
б) 
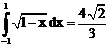
ErrHauss3=-3.3*10-10 ErrHauss4=-3.6*10-15 ErrSimps=-0.00359 m=2
ErrNewtCot3=0.000377 ErrNewtCot4=7.3*10-6 ErrAtk=4.3*10-6 p=1.50
--------------------------------------------------------------------------------------------------------------------
6. а)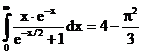 
б) 
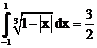
ErrHauss3=-0.000132 ErrHauss4=0.0000410 ErrSimps=-0.0171 m=2
ErrNewtCot3=-0.00144 ErrNewtCot4=0.00602 ErrAtk=0.0000603 p=1.33
--------------------------------------------------------------------------------------------------------------------
7. а)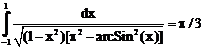 
б) 
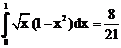
ErrHauss3=-0.00676 ErrHauss4=-0.00388 ErrSimps=-0.00127 m=2
ErrNewtCot3=0.0301 ErrNewtCot4=0.0238 ErrAtk=0.0000212 p=1.48
--------------------------------------------------------------------------------------------------------------------
8. а)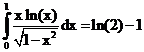 
б) 
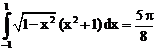
ErrHauss3=-0.00369 ErrHauss4=-0.00148 ErrSimps=-0.0209 m=2
ErrNewtCot3=0.0401 ErrNewtCot4=0.0252 ErrAtk=-0.00194 p=1.64
--------------------------------------------------------------------------------------------------------------------
9. а)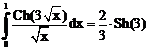 
б) 
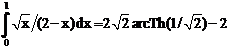
ErrHauss3=-9.6*10-7 ErrHauss4=-1.1*10-10 ErrSimps=-0.000630 m=2
ErrNewtCot3=-0.0232 ErrNewtCot4=0.00173 ErrAtk=0.0000398 p=1.43
--------------------------------------------------------------------------------------------------------------------
10. а)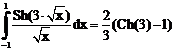 
б) 
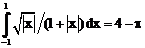
ErrHauss3=0.0569 ErrHauss4=0.0333 ErrSimps=-0.00735 m=2
ErrNewtCot3=-0.324 ErrNewtCot4=-0.201 ErrAtk=-0.000308 p=1.58
--------------------------------------------------------------------------------------------------------------------
11. а)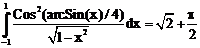 
б) 
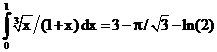
ErrHauss3=0.0163 ErrHauss4=0.00913 ErrSimps=-0.00342 m=2
ErrNewtCot3=-0.0735 ErrNewtCot4=-0.0574 ErrAtk=-0.0000614 p=1.36
--------------------------------------------------------------------------------------------------------------------
12. а)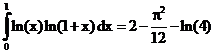 
б) 
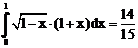
ErrHauss3=-0.00200 ErrHauss4=-0.000676 ErrSimps=-0.00255 m=2
ErrNewtCot3=0.0214 ErrNewtCot4=0.0126 ErrAtk=-0.0000273 p=1.52
--------------------------------------------------------------------------------------------------------------------
13. а)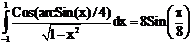 
б) 
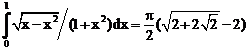
ErrHauss3=0.00876 ErrHauss4=0.00492 ErrSimps=-0.00190 m=2
ErrNewtCot3=-0.0394 ErrNewtCot4=-0.0309 ErrAtk=-0.0000260 p=1.49
-------------------------------------------------------------------------------------------------------------------
14. а)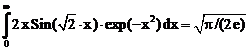 
б) 
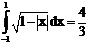
ErrHauss3=0.000240 ErrHauss4=-6.1*10-6 ErrSimps=-0.00717 m=2
ErrNewtCot3=0.0106 ErrNewtCot4=0.00552 ErrAtk=0.0000411 p=1.49
-------------------------------------------------------------------------------------------------------------------
15. а)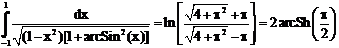 
б) 
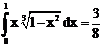
ErrHauss3=0.0268 ErrHauss4=0.00118 ErrSimps=-0.00431 m=2
ErrNewtCot3=-0.0524 ErrNewtCot4=-0.0555 ErrAtk=-0.0000770 p=1.36
-------------------------------------------------------------------------------------------------------------------
16. а)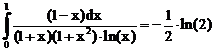 
б) 
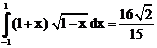
ErrHauss3=-0.00222 ErrHauss4=-0.00113 ErrSimps=-0.00725 m=2
ErrNewtCot3=0.0484 ErrNewtCot4=0.0337 ErrAtk=-0.000158 p=1.54
--------------------------------------------------------------------------------------------------------------------
17. а)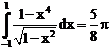 
б) 
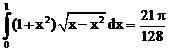
ErrHauss3=0. ErrHauss4=0. ErrSimps=-0.00386 m=2
ErrNewtCot3=-0.393 ErrNewtCot4=-0.218 ErrAtk=-0.000160 p=1.56
--------------------------------------------------------------------------------------------------------------------
18. а)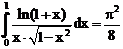 
б) 
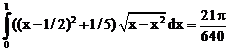
ErrHauss3=-7.5*10-6 ErrHauss4=-1.7*10-7 ErrSimps=-0.00118 m=2
ErrNewtCot3=-0.000354 ErrNewtCot4=0.000252 ErrAtk=-0.000118 p=1.65
--------------------------------------------------------------------------------------------------------------------
19. а)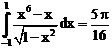 
б) 
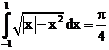
ErrHauss3=-0.0982 ErrHauss4=0. ErrSimps=-0.0145 m=2
ErrNewtCot3=0.589 ErrNewtCot4=0.395 ErrAtk=-0.000181 p=1.53
--------------------------------------------------------------------------------------------------------------------
20. а)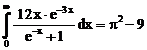 
б) 
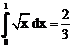
ErrHauss3=-0.0000237 ErrHauss4=5.9*10-6 ErrSimps=-0.00127 m=2
ErrNewtCot3=0.00361 ErrNewtCot4=0.00510 ErrAtk=1.5*10-6 p=1.53
--------------------------------------------------------------------------------------------------------------------
21. а)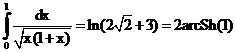 
б) 
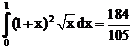
ErrHauss3=-0.0000171 ErrHauss4=-4.4*10-7 ErrSimps=-0.00124 m=2
ErrNewtCot3=0.00246 ErrNewtCot4=0.000505 ErrAtk=0.0000511 p=1.44
--------------------------------------------------------------------------------------------------------------------
22. а)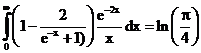 
б) 
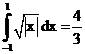
ErrHauss3=-0.0000328 ErrHauss4=-1.2*10-6 ErrSimps=-0.00717 m=2
ErrNewtCot3=0.00191 ErrNewtCot4=0.00185 ErrAtk=0.0000411 p=1.49
--------------------------------------------------------------------------------------------------------------------
23. а)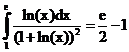 
б) 
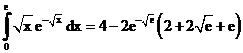
ErrHauss3=0.00142 ErrHauss4=0.000188 ErrSimps=-0.00560 m=2
ErrNewtCot3=-0.0169 ErrNewtCot4=-0.00902 ErrAtk=0.000192 p=1.45
--------------------------------------------------------------------------------------------------------------------
24. а)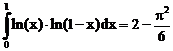 
б) 
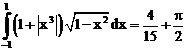
ErrHauss3=0.00349 ErrHauss4=0.00126 ErrSimps=-0.0212 m=2
ErrNewtCot3=-0.0348 ErrNewtCot4=-0.0210 ErrAtk=-0.00326 p=1.74
--------------------------------------------------------------------------------------------------------------------
25. а)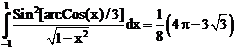 
б) 
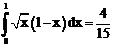
ErrHauss3=-0.0134 ErrHauss4=-0.00748 ErrSimps=-0.00128 m=2
ErrNewtCot3=0.0605 ErrNewtCot4=0.0472 ErrAtk=-0.0000279 p=1.54
--------------------------------------------------------------------------------------------------------------------
а)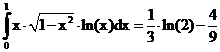 
б) 
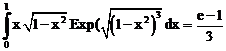
ErrHauss3=-0.00150 ErrHauss4=-0.000569 ErrSimps=-0.00181 m=2
ErrNewtCot3=0.0133 ErrNewtCot4=0.00837 ErrAtk=0.000255 p=1.54
--------------------------------------------------------------------------------------------------------------------
26. а)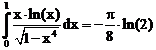 
б) 
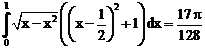
ErrHauss3=-0.00303 ErrHauss4=-0.00122 ErrSimps=-0.00322 m=2
ErrNewtCot3=0.0336 ErrNewtCot4=0.0209 ErrAtk=-0.000152 p=1.57
-------------------------------------------------------------------------------------------------------------------- а)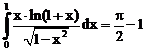 
б) 
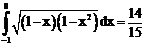
ErrHauss3=-0.0000119 ErrHauss4=-2.5*10-7 ErrSimps=-0.00255 m=2
ErrNewtCot3=-0.00112 ErrNewtCot4=0.000501 ErrAtk=-0.0000273 p=1.52
--------------------------------------------------------------------------------------------------------------------
27. а)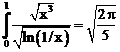 
б) 
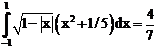
ErrHauss3=-0.000162 ErrHauss4=-0.0000381 ErrSimps=-0.00894 m=2
ErrNewtCot3=-0.00241 ErrNewtCot4=0.00164 ErrAtk=-0.000753 p=1.64
--------------------------------------------------------------------------------------------------------------------а)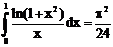 
б) 
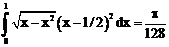
ErrHauss3=0.0000208 ErrHauss4=5.6*10-7 ErrSimps=-0.000669 m=2
ErrNewtCot3=0.00182 ErrNewtCot4=0.000786 ErrAtk=-0.0000988 p=1.74
--------------------------------------------------------------------------------------------------------------------
28. а)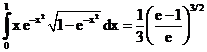 
б) 
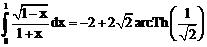
ErrHauss3=0.000142 ErrHauss4=-4.9*10-6 ErrSimps=-0.000630 m=2
ErrNewtCot3=0.00332 ErrNewtCot4=0.00133 ErrAtk=0.0000398 p=1.43
--------------------------------------------------------------------------------------------------------------------
29. а)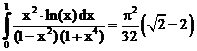 
б) 
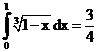
ErrHauss3=0.000325 ErrHauss4=0.0000266 ErrSimps=-0.00339 m=2
ErrNewtCot3=-0.00597 ErrNewtCot4=-0.00302 ErrAtk=2.3*10-6 p=1.33
--------------------------------------------------------------------------------------------------------------------
30. а)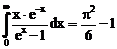 
б) 
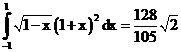
ErrHauss3=0.000326 ErrHauss4=-0.0000128 ErrSimps=-0.0147 m=2
ErrNewtCot3=0.0399 ErrNewtCot4=0.0170 ErrAtk=-0.000783 p=1.58
-------------------------------------------------------------------------------------------------------------------
31. а)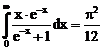 
б) 
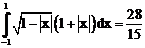
ErrHauss3=-0.00218 ErrHauss4=-0.000632 ErrSimps=-0.0145 m=2
ErrNewtCot3=-0.0482 ErrNewtCot4=-0.0235 ErrAtk=-0.000229 p=1.53
-------------------------------------------------------------------------------------------------------------------
32. а)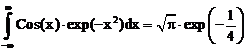 
б) 
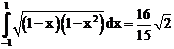
ErrHauss3=0.00164 ErrHauss4=-0.0000587 ErrSimps=-0.0725 m=2
ErrNewtCot3=0.00164 ErrNewtCot4=-0.00410 ErrAtk=-0.000158 p=1.54
-------------------------------------------------------------------------------------------------------------------
33. а)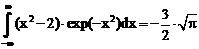 
б) 
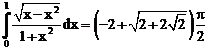
ErrHauss3=0. ErrHauss4=0. ErrSimps=-0.00190 m=2
ErrNewtCot3=0. ErrNewtCot4=0. ErrAtk=0.0000260 p=1.49
-------------------------------------------------------------------------------------------------------------------
34. а)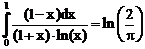 
б) 
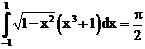
ErrHauss3=-0.00234 ErrHauss4=-0.00114 ErrSimps=-0.0102 m=2
ErrNewtCot3=0.0476 ErrNewtCot4=-0.0334 ErrAtk=-0.0000970 p=1.52
-------------------------------------------------------------------------------------------------------------------
35. а)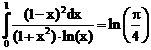 
б) 
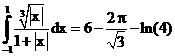
ErrHauss3=-0.00211 ErrHauss4=-0.00113 ErrSimps=-0.0173 m=2
ErrNewtCot3=0.0492 ErrNewtCot4=-0.0339 ErrAtk=-0.000309 p=1.37
--------------------------------------------------------------------------------------------------------------------
36. а)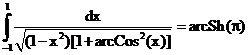 
б) 
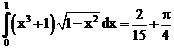
ErrHauss3=0.00141 ErrHauss4=0.00194 ErrSimps=-0.00366 m=2
ErrNewtCot3=0.00489 ErrNewtCot4=0.000219 ErrAtk=-0.000258 p=1.60
--------------------------------------------------------------------------------------------------------------------
37. а)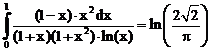 
б) 
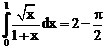
ErrHauss3=-0.000117 ErrHauss4=-1.8*10-6 ErrSimps=-0.00128 m=2
ErrNewtCot3=-0.000777 ErrNewtCot4=-0.000222 ErrAtk=-0.0000405 p=1.55
-------------------------------------------------------------------------------------------------------------------
38. а)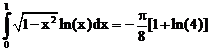 
б) 
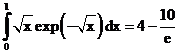
ErrHauss3=-0.000301 ErrHauss4=-0.0000894 ErrSimps=-0.00126 m=2
ErrNewtCot3=-0.0162 ErrNewtCot4=0.0103 ErrAtk=0.0000170 p=1.48
-------------------------------------------------------------------------------------------------------------------
39. а)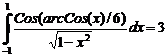 
б) 
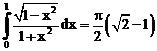
ErrHauss3=0.00381 ErrHauss4=0.00214 ErrSimps=-0.000890 m=2
ErrNewtCot3=-0.0171 ErrNewtCot4=-0.0134 ErrAtk=0.0000123 p=1.48
-------------------------------------------------------------------------------------------------------------------
40. а)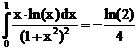 
б) 
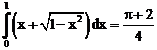
ErrHauss3=-0.00116 ErrHauss4=-0.000655 ErrSimps=-0.00180 m=2
ErrNewtCot3=0.0254 ErrNewtCot4=0.0135 ErrAtk=0.0000101 p=1.51
-------------------------------------------------------------------------------------------------------------------
41. а)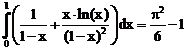 
б) 
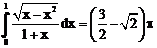
ErrHauss3=-0.00150 ErrHauss4=-0.000572 ErrSimps=-0.00192 m=2
ErrNewtCot3=0.0142 ErrNewtCot4=0.00878 ErrAtk=-0.0000587 p=1.55
-------------------------------------------------------------------------------------------------------------------
42. а)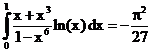 
б) 
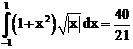
ErrHauss3=-0.00214 ErrHauss4=-0.000642 ErrSimps=-0.00720 m=2
ErrNewtCot3=0.0166 ErrNewtCot4=0.0106 ErrAtk=-0.000298 p=1.55
-------------------------------------------------------------------------------------------------------------------
43. а)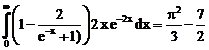 
б) 
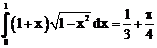
ErrHauss3=0.000132 ErrHauss4=-0.0000410 ErrSimps=-0.00362 m=2
ErrNewtCot3=0.00144 ErrNewtCot4=-0.00602 ErrAtk=-0.0000615 p=1.53
-------------------------------------------------------------------------------------------------------------------
44. а)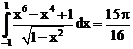 
б) 
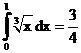
ErrHauss3=-0.0982 ErrHauss4=0. ErrSimps=-0.00339 m=2
ErrNewtCot3=0.196 ErrNewtCot4=0.177 ErrAtk=2.3*10-6 p=1.33
--------------------------------------------------------------------------------------------------------------------
45. а)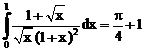 
б) 
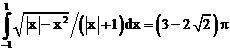
ErrHauss3=0.0220 ErrHauss4=0.0122 ErrSimps=-0.0110 m=2
ErrNewtCot3=-0.109 ErrNewtCot4=-0.0769 ErrAtk=-0.000445 p=1.58
--------------------------------------------------------------------------------------------------------------------
46. а)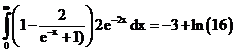 
б) 
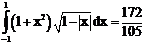
ErrHauss3=-0.00003423 ErrHauss4=-0.0000317 ErrSimps=-0.0147 m=2
ErrNewtCot3=-0.00413 ErrNewtCot4=-0.0114 ErrAtk=-0.000798 p=1.59
--------------------------------------------------------------------------------------------------------------------
47. а)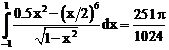 
б) 
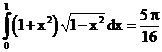
ErrHauss3=-0.00153 ErrHauss4=0. ErrSimps=-0.00364 m=2
ErrNewtCot3=-0.00920 ErrNewtCot4=-0.00617 ErrAtk=-0.000152 p=1.56
-------------------------------------------------------------------------------------------------------------------
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Решение задачи Коши
Задача Коши или начальная задача для системы дифференциальных уравнений
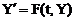, (1)
где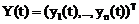 
– неизвестный вектор, 
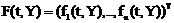– вектор-функция, состоит в нахождении решения системы, удовлетворяющего начальным условиям:
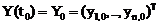(2)
Дифференциальное уравнение n-го порядка,
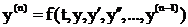
сводится к системе (1) с помощью подстановок:
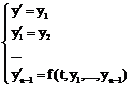
При численном решении задачи Коши рассматривается последовательность точек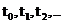 
, в общем случае, с переменной длиной шага 
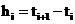. В каждой точке 
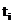решение системы 
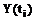аппроксимируется вектором 
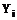, значение которого вычисляется по найденным значениям в предыдущих точках 
.
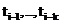Погрешность аппроксимации, возникающая на каждом шаге, может быть описана следующим образом. Пусть рассматривается дифференциальное уравнение:
,
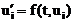где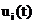 
- точное решение уравнения, удовлетворяющее условию: 
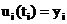. Локальной ошибкой дискретизации называется величина:
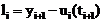
Численный метод имеет порядок точности p, если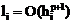 
.
Рассмотрим методы решения задачи Коши на примере уравнения первого порядка
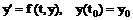. (3)
Отметим, что все изло