Закон распределения дискретной случайной величины.

Если возможными значениями дискретной случайной величины 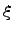являются 0, 1, 2, …, n, а соответствующие им вероятности вычисляются по формуле Бернулли:

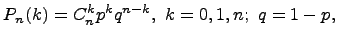
то говорят, что случайная величина 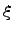имеет биномиальный закон распределения:

64. Испытания Бернулли

Формула Бернулли — формула в теории вероятностей, позволяющая находить вероятность появления события A при независимых испытаниях. Формула Бернулли позволяет избавиться от большого числа вычислений — сложения и умножения вероятностей — при достаточно большом количестве испытаний. Названа в честь выдающегося швейцарского математика Якоба Бернулли, выведшего формулу.

Формулировка

Теорема: Если Вероятность p наступления события Α в каждом испытании постоянна, то вероятность 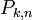того, что событие A наступит k раз в n независимых испытаниях, равна: , где .

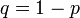[Доказательство

Так как в результате 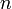независимых испытаний, проведенных в одинаковых условиях, событие 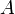наступает с вероятностью 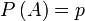, следовательно противоположное ему событие с вероятностью .

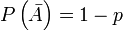Обозначим 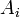— наступление события 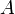в испытании с номером 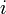. Так как условия проведения опытов одинаковые, то эти вероятности равны. Пусть в результате 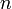опытов событие 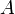наступает 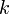раз, тогда остальные раз это событие не наступает. Событие 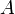может появиться 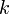раз в 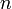испытаниях в различных комбинациях, число которых равно количеству сочетаний из 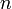элементов по 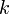. Это количество сочетаний находится по формуле:

.

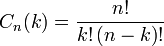При этом вероятность каждой комбинации равна произведению вероятностей:

.

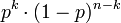Применяя теорему сложения вероятностей несовместных событий, получим окончательную Формулу Бернулли:

, где .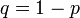

Схема испытаний Бернулли

Пусть один и тот же опыт повторяется п раз, испытания независимы, в результате каждого испытания может наступить или нет событие А. Пусть Р(А) = р — вероятность наступления А, тогда 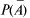= q = 1 - р. Такая схема испытаний называется схемой Бернулли. Найдем вероятность 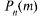того, что событие А произойдет при n испытаниях m раз.

Пространство элементарных событий состоит из произведений п событий А или 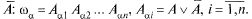Событие

В, состоящее в том, что событие А произойдет при п испытаниях т раз, включает те 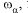в которых А содержится 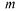раз, их 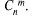По формуле (34.7) 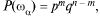поэтому по (34.3)

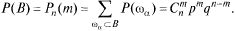
Формула 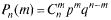(34.10) называется формулой Бернулли.

Пример: Найти вероятность того, что четырехзначный номер первого встречного автомобиля содержит две цифры 5.

Так как 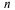= 4 (число цифр в номере), 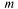= 2, событие А — данная цифра номера 5, 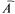— не 5, Р(А) = 1/10, 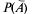= 9/10, то

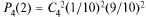= 6 · 0,01· 0,81 = 0,0486

При больших значениях подсчет проводится по при-

ближенной формуле (локальная теорема Лапласа)

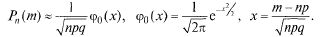
Если 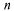велико, а 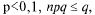то применяют приближенную

формулу Пуассона:

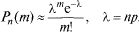
65. Математическое ожидание дискретной величины, его свойства

МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ [ mathematical expectation ]

Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности: M(X) = x₁ p₁+ x₂ p₂+...+ x_n p_n.
Реально на основе данных выборки мы не можем вычислить M(X). Однако эту характеристику можно оценить. В качествеоценки можно использовать среднее арифметическое, то есть M(X) ≈`X. Чем больше объём выборки (число наблюдений), тем точнее эта оценка. Математическое ожидание обладает следующими свойствами:
1. Математическое ожидание постоянной величины равно самой постоянной: M(C) = C.
2. Постоянный множитель можно выносить за знак математического ожидания: M(CX) = CM(X).
3. Математическое ожидание суммы нескольких случайных величин равно сумме математических ожиданий слагаемых: M(X+Y+Z) = M(X)+M(Y)+M(Z).
4. Математическое ожидание произведения нескольких взаимно независимых случайных величин равно произведению их математических ожиданий: M(X×Y×Z) = M(X)×M(Y)×M(Z). Все эти свойства имеют большое практическое значение.

Математи́ческое ожида́ние — среднее значение случайной величины, распределение вероятностей случайной величины, рассматривается в теории вероятностей.^[1] В англоязычной литературе и в математическом сообществе Санкт-Петербурга обозначается через 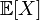(например, от англ. Expectedvalue или нем. Erwartungswert), в русской — 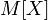(возможно, отангл. Meanvalue или нем. Mittelwert, а возможно от рус. Математическое ожидание). В статистике часто используют обозначение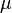

Определение

Пусть задано вероятностное пространство 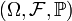и определённая на нём случайная величина 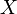. То есть, по определению, 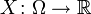— измеримая функция. Если существуетинтеграл Лебега от 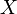по пространству 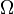, то он называется математическим ожиданием, или средним (ожидаемым) значением и обозначается 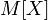или .

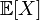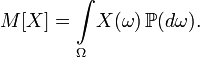
Дискретные распределения

Определение 3. Случайная величина называется простой или дискретной, если она принимает не более, чем счётное число значений. То есть 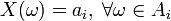, где 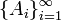— разбиение .

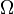Распределение простой случайной величины тогда по определению задаётся: 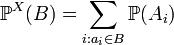. Введя обозначение 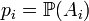, можно задать функцию 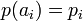. Очевидно, что 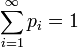. Используя счётную аддитивность 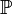, легко показать, что эта функция однозначно определяет распределение .

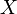Определение 4. Функция 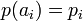, где 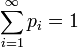часто называется дискретным распределением.

Пример 1. Пусть функция 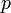задана таким образом, что 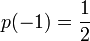и 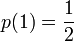. Эта функция задаёт распределение случайной величины 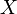такой, что 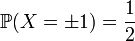(распределение Бернулли).

Теорема 3. Дискретное распределение обладает следующими свойствами:

1. ;

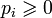2. .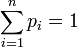