Аппроксимация функции с помощью Excel
Для проведения расчетов, данные целесообразно расположить в виде таблицы (рис.2), используя средства табличного процессора MS Excel.
Рис.2 Фрагмент рабочего листа MS Excel в режиме отображения данных для линейной аппроксимации
Поясним как таблица (рис.2) составляется:
Шаг 1. В ячейки B2:B26 заносим значения 
.
Шаг 2. В ячейки С2:С26 заносим значения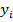 
.
Шаг 3. В ячейки D2 вводим формулу = В2^2.
Шаг 4. В ячейки D3:D26 эта формула копируется.
Шаг 5. В ячейку Е2 вводим формулу = В2*С2.
Шаг 6. В ячейки Е3:Е26 эта формула копируется.
Шаг 7. В ячейку F2 вводим формулу = В2^3.
Шаг 8. В ячейки F3:F26 эта формула копируется.
Шаг 9. В ячейку G2 вводим формулу = G2^4.
Шаг 10. В ячейки G3: G26 эта формула копируется.
Шаг 11. В ячейку H2 вводим формулу = В2^2* С2.
Шаг 12. В ячейки H3: H26 эта формула копируется.
Шаг 13. В ячейку I2 вводим формулу =Ln(C2).
Шаг 14. В ячейки I3: I26 эта формула копируется.
Шаг 15. В ячейку J2 вводим формулу =В2* Ln(C2).
Шаг 16. В ячейки J3: J26 эта формула копируется.
Следующие шаги делаем с помощью автосуммирования Σ.
Шаг 17. В ячейку В27 вводим формулу =СУММ(В2:В26).
Шаг 18. В ячейку C27 вводим формулу = СУММ(C2: C26).
Шаг 19. В ячейку D27 вводим формулу = СУММ(D2: D26).
Шаг 20. В ячейку E27 вводим формулу = СУММ(Е2: Е26).
Шаг 21. В ячейку F27 вводим формулу =СУММ(F2: F26).
Шаг 22. В ячейку G27 вводим формулу =СУММ(G2: G26).
Шаг 23. В ячейку H27 вводим формулу = СУММ(Н2: Н26).
Шаг 24. В ячейку I27 вводим формулу = СУММ(I2: I26).
Шаг 25. В ячейку J27 вводим формулу = СУММ(J2: J26).
Аппроксимируем функцию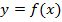 
линейной функцией 
.
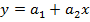Используя итоговые суммы (рис.2), находящиеся в ячейках В27, C27, D27 и Е27, запишем систему в виде:
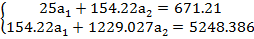
Решив её методом обратной матрицы, получим,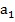 
=2,2370 и 
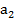= 3,9897.
Таким образом, линейная аппроксимация имеет вид y=-2,2370+3,9897x.
Система уравнений решена средствами MS Excel. Фрагмент рабочего листа с выполненными расчетами представлен на рис.3. Матрица, соответствующая системе уравнений, расположена в интервале ячеек A30:C31. Элементами матрицы являются значения сумм.
Рис.3. Фрагмент рабочего листа в режиме отображения данных с результатами расчетов коэффициентов линейной аппроксимации
На рисунке 3 в ячейках А34:В35 записана формула {=МОБР(А30:В31)}
В ячейках Е34:Е35 записана формула {=МУМНОЖ(А34:В35;С30:С31)}
Далее аппроксимируем функцию 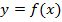квадратичной функцией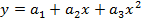 
Используя итоговые суммы на рис.2, расположенные в ячейках В27, С27, D27, E27, F27, G27 и H27 запишем систему в виде:
решив которую, получим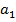 
=2,54564 
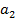=3,851584и 
=0,011048.
Таким образом, квадратичная аппроксимация имеет вид y=2,54564 +3,851584x+0,011048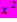 
Решение системы проводили, пользуясь средствами Microsoft Excel. Результаты представлены на рис.4.
Рис.4. Фрагмент рабочего листа в режиме отображения данных с результатами расчетов коэффициентов квадратичной аппроксимации
В рис.4 в ячейках А43:С435 записана формула {=МОБР(А38:С40)}
В ячейках F43:F45 записана формула {=МУМНОЖ(А43:С45;D38:D40}
Теперь аппроксимируем функцию в 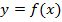в экспоненциальной функцией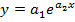 
Для определения коэффициентов 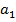и 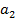прологарифмируем значения 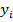и, используя готовые суммы рис.2, расположенные в ячейках В27, D27, I27 и J27, получим систему:
где с = 
.
Решив систему, найдем с=2,453832299 и 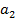=0,124989592.
После потенцирования получим 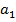=11,63284194.
Таким образом, экспоненциальная аппроксимация имеет вид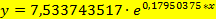 
Результаты расчетов представлены на рис.5.
Рис.5. Фрагмент рабочего стола в режиме отображения формул с результатами расчетов коэффициентов экспоненциальной аппроксимации
На рис.5 в ячейках А52:В53 записана формула {=МОБР(А48:В49)}.
В ячейках E451:E52 записана формула {=МУМНОЖ(А52:В53;С48:С49}.
В ячейке E53 записана формула =EXP(E51).
Вычислим средние арифметическое х и у по формулам:
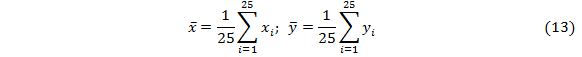
Результаты расчета 
и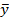 
представлены на рис 6.
Рис 6. Фрагмент рабочего листа в режиме отображения данных с результатами вычисления среднего арифметического и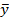
В ячейке В56 записана формула =В27/25.
В ячейку В57 записана формула =С27/25.