Раздел 5 Основы теории вероятности и математической статистики

Содержание

Виды случайных событий. Понятие вероятности. Операции над событиями. Теоремы сложения и умножения вероятностей. Формула полной вероятности. Схема независимых испытаний. Формула Бернулли. Элементы комбинаторного анализа: размещения, перестановки, сочетания.

Основные задачи математической статистики. Основные понятия математической статистики: генеральная совокупность и выборка. Статистическое распределение. Гистограмма. Полигон. Оценка параметров генеральной совокупности по ее выборке. Интервальная оценка. Доверительный интервал и доверительная вероятность.

Вопросы для самоконтроля

1. Что такое комбинаторика?

2. Что такое перестановки?

3. Как вычислить количество перестановок?

4. Что такое размещения?

5. Как вычислить количество размещений?

6. Что такое сочетания?

7. Как вычислить количество сочетаний?

8. Какое событие называется достоверным?

9. Как обозначается достоверное событие?

10. Какое событие называется невозможным?

11. Как обозначается невозможное событие?

12. Какое событие называется случайным?

13. Как обозначается случайное событие?

14. Какие события называют несовместными?

15. Какое событие называют противоположным данному событию?

16. Что такое сумма событий?

17. Что такое произведение событий?

18. Что называют испытанием или опытом?

19. Какое событие называют элементарным?

20. Как обозначаются элементарные события?

21. Что изучает теория вероятностей?

22. Как классически определяется вероятность?

23. Какова вероятность достоверного события?

24. Какова вероятность невозможного события?

25. Каков диапазон вероятностной оценки случайного события?

26. Как статистически определяется вероятность?

27. В чем заключается правило сложения вероятностей?

28. В чем заключается правило умножения совместных случайных событий?

29. В чем заключается правило умножения независимых случайных событий?

30. Как определяется полная вероятность попарно несовместных событий?

31. Назовите основные задачи математической статистики.

32. Что такое генеральная совокупность?

33. Что такое выборка?

34. Что такое статистическое распределение?

35. Как построить гистограмму?

36. Что такое полигон частот?

37. Как найти математическое ожидание?

38. Как найти среднее квадратическое отклонение?

39. Что такое интервальная оценка?

40. Что такое доверительный интервал?

41. Что такое доверительная вероятность?

Раздел 6 Основы дискретной математики

Содержание

Сложные высказывания.Логические операции: отрицание или инверсия, дизъюнкция, конъюнкция, строгая дизъюнкция, импликация, эквиваленция. Словарь перевода на язык алгебры логики. Необходимое и достаточное условие импликации. Формулы алгебры логики. Законы алгебры. Логические функции. Определение булевой функции. Равенство функций. Определение формулы. Определение композиции двух булевых функций. Булевы функции. Определение инверсии. Булевы функции двух переменных. Способы задания булевых функций. Разложение функций по переменным. Нормальные формы. Логические схемы. Язык логики предикатов. Логические операции над предикатами. Кванторы. Правила вывода исчисления предикатов. Отрицания в исчислении предикатов

Вопросы для самоконтроля

1. Что называют высказыванием.

2. Как определяется формула алгебры логики.

3. Что представляют собой таблицы истинности.

4. Что такое конъюнкция.

5. Что такое дизъюнкция.

6. Что такое импликация.

7. Что такое эквиваленция.

8. Что такое булева функция.

9. Перечислите тождества.

10. Что такое предикат.

11. Что такое квантор всеобщности.

12. Что такое квантор существования.

13. Что такое предикатная формула.

ПЕРЕЧЕНЬ РЕКОМЕНДУЕМЫХ УЧЕБНЫХ ИЗДАНИЙ, ИНТЕРНЕТ-РЕСУРСОВ, ДОПОЛНИТЕЛЬНОЙ ЛИТЕРАТУРЫ

Основные источники

1. Григорьев, В.П. Элементы высшей математики: учебник для студентов учреждений среднего профессионального образования / В.П. Григорьев, Ю.А. Дубинский.- М.: Издательский центр «Академия», 2013.

Дополнительные источники

1.Высшая математика: учебник и практикум для академического бакалавриата / М.Б. Хрипунова [и др.]; под общ. ред. М.Б. Хрипуновой, И.И. Цыганок [Электронный ресурс]. – М.: Издательство Юрайт, 2017.

2.Красс, М.С. Математика в экономике: математические методы и модели: учебник для бакалавров / М.С. Красс, Б.П. Чупрынов; под ред. М.С. Красс [Электронный ресурс]. – М.: Издательство Юрайт, 2017.

3.Кремер, Н.Ш. Элементы линейной алгебры: учебник и практикум для СПО / Н.Ш. Кремер, М.Н. Фридман; под ред. Н.Ш. Кремера [Электронный ресурс]. – М.: Издательство Юрайт, 2017.

4.Макаров, С.И. Математика для экономистов: учебное пособие/С.И. Макаров [Электронный ресурс]. - М.: КНОРУС, 2016.

5.Математика для экономистов Задачник: учебно-практическое пособие /коллектив авторов; под ред. С.И. Макарова, М.В. Мищенко. – М.: КНОРУС, 2016.

6.Седых, И.Ю. Математика: учебник и практикум для СПО / И.Ю. Седых, Ю.Б. Гребенщиков, А.Ю. Шевелев [Электронный ресурс]. – М.: Издательство Юрайт, 2016.

Периодические издания:

Журналы

1. Потенциал [Электронный ресурс]

2. Математика и ее приложения [Электронный ресурс].

3. Фундаментальная и прикладная математика [Электронный ресурс].

Интернет-ресурсы

1. http://www.ict.edu.ru/

2. http://www.itpedia.ru

3. http://www.exponenta.ru/

4. http://reshebnik.ru/solutions/

5. http://college.ru/matematika/

6. http://www.etudes.ru

7. http://www.uztest.ru

8. http://www.kvant.info

ЗАДАНИЯ ДЛЯ КОНТРОЛЬНОЙ РАБОТЫ

Вариант 1

1. Решить систему уравнений по формулам Крамера

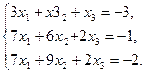
2. Вычислить пределы функций

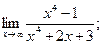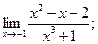1) 2) 3)

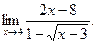
3. Вычислить производные функций

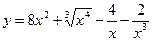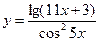1) ; 2) ; 3) .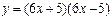

4. Провести полное исследование функции и построить ее график

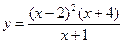
5. Вычислить неопределенный интеграл

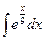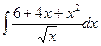1) ; 2) ; 3) .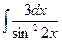

6. Вычислить определенный интеграл

1) 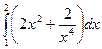; 2) 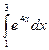; 3) Вычислить площадь фигуры, ограниченной графиками функций , .

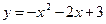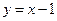7. Даны числа , , ,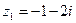

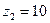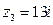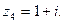
1. Изобразить на числовой плоскости

2. Найти модули и аргументы чисел 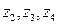. Записать 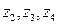в тригонометрической форме.

3. Вычислить , , .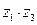

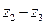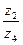Вариант 2

1. Решить систему уравнений по формулам Крамера

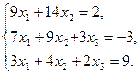
2. Вычислить пределы функций

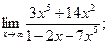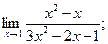1) 2) 3)

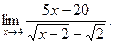
3. Вычислить производные функций

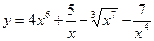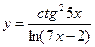1) ; 2) ; 3)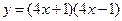

4. Провести полное исследование функции и построить ее график

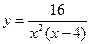
5. Вычислить неопределенный интеграл

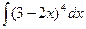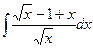1) ; 2) ; 3)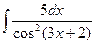

6. Вычислить определенный интеграл

1) 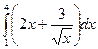; 2) 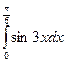; 3) Вычислить площадь фигуры, ограниченной графиками функций , .

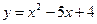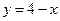7. Даны числа , , ,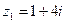

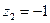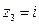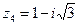
1. Изобразить на числовой плоскости

2. Найти модули и аргументы чисел 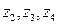. Записать 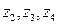в тригонометрической форме.

3. Вычислить , , .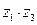

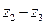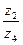Вариант 3

1. Решить систему уравнений по формулам Крамера

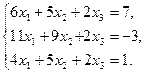
2. Вычислить пределы функций

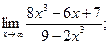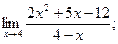1) 2) 3)

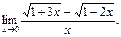
3. Вычислить производные функций

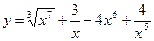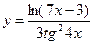1) ; 2) ; 3) .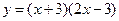

4. Провести полное исследование функции и построить ее график

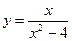
5. Вычислить неопределенный интеграл

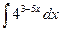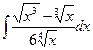1) ; 2) ; 3) .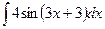

6. Вычислить определенный интеграл

1) 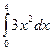; 2) 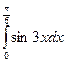; 3) Вычислить площадь фигуры, ограниченной графиками функций ,

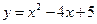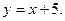
7. Даны числа , , ,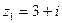

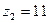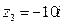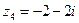
1. Изобразить на числовой плоскости

2. Найти модули и аргументы чисел 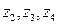. Записать 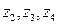в тригонометрической форме.

3. Вычислить , , .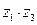

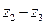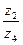Вариант 4

1. Решить систему уравнений по формулам Крамера

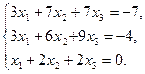
2. Вычислить пределы функций

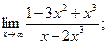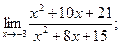1) 2) 3)

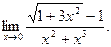
3. Вычислить производные функций

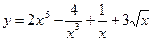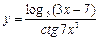1) ; 2) ; 3) .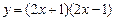

4. Провести полное исследование функции и построить ее график

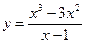
5. Вычислить неопределенный интеграл

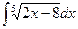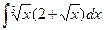1) ; 2) ; 3) .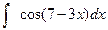

6. Вычислить определенный интеграл

1) 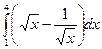; 2) 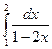; 3) Вычислить площадь фигуры, ограниченной графиками функций , .

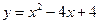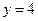7. Даны числа , , ,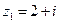

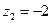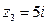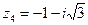
1. Изобразить на числовой плоскости

2. Найти модули и аргументы чисел 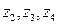. Записать 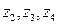в тригонометрической форме.

3. Вычислить , , .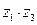

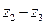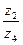Вариант 5

1. Решить систему уравнений по формулам Крамера

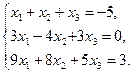
2. Вычислить пределы функций

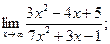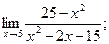1) 2) 3)

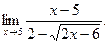
3. Вычислить производные функций

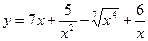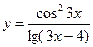1) ; 2) ; 3) .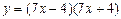

4. Провести полное исследование функции и построить ее график

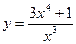
5. Вычислить неопределенный интеграл

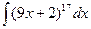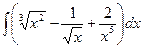1) ; 2) ; 3) .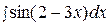

6. Вычислить определенный интеграл

1) 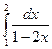; 2) 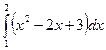; 3) Вычислить площадь фигуры, ограниченной графиками функций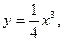

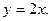
7. Даны числа , , ,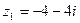

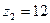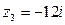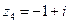
1. Изобразить на числовой плоскости

2. Найти модули и аргументы чисел 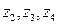. Записать 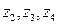в тригонометрической форме.

3. Вычислить , , .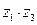

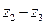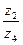Вариант 6

1. Решить систему уравнений по формулам Крамера

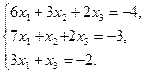
2. Вычислить пределы функций

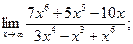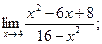1) 2) 3)

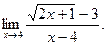
3. Вычислить производные функций

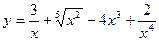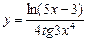1) ; 2) ; 3) .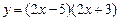

4. Провести полное исследование функции и построить ее график

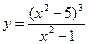
5. Вычислить неопределенный интеграл

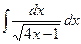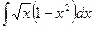1) ; 2) ; 3) .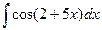

6. Вычислить определенный интеграл

1) 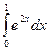; 2) 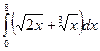; 3) Вычислить площадь фигуры, ограниченной графиками функций , .

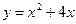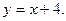7. Даны числа , , ,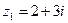

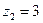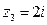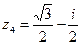
1. Изобразить на числовой плоскости

2. Найти модули и аргументы чисел 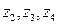. Записать 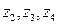в тригонометрической форме.

3. Вычислить , , .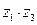

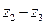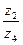Вариант 7

1. Решить систему уравнений по формулам Крамера

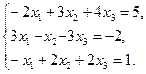
2. Вычислить пределы функций

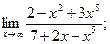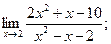1) 2) 3)

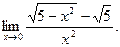
3. Вычислить производные функций

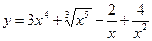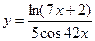1) ; 2) ; 3)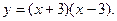

4. Провести полное исследование функции и построить ее график

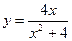
5. Вычислить неопределенный интеграл

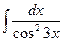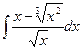1) ; 2) ; 3) .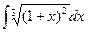

6. Вычислить определенный интеграл

1) 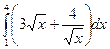; 2) 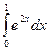; 3) Вычислить площадь фигуры, ограниченной графиками функций , .

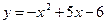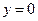7. Даны числа , , ,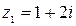

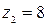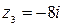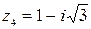
1. Изобразить на числовой плоскости

2. Найти модули и аргументы чисел 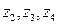. Записать 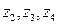в тригонометрической форме.

3. Вычислить , , .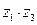

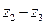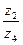Вариант 8

1. Решить систему уравнений по формулам Крамера

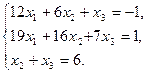
2. Вычислить пределы функций

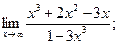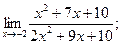1) 2) 3)

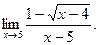
3. Вычислить производные функций

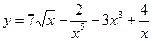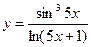1) ; 2) ; 3) .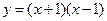

4. Провести полное исследование функции и построить ее график

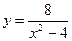
5. Вычислить неопределенный интеграл

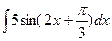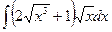1) ; 2) ; 3) .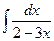

6. Вычислить определенный интеграл

1) 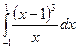; 2) 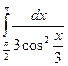; 3) Вычислить площадь фигуры, ограниченной графиками функций ,

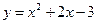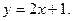
7. Даны числа , , ,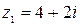

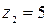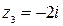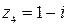
1. Изобразить на числовой плоскости

2. Найти модули и аргументы чисел 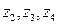. Записать 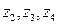в тригонометрической форме.

3. Вычислить , , .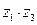

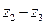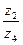Вариант 9

1. Решить систему уравнений по формулам Крамера

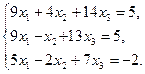
2. Вычислить пределы функций

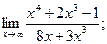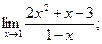1) 2) 3)

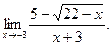
3. Вычислить производные функций

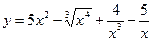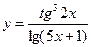1) ; 2) ; 3)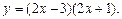

4. Провести полное исследование функции и построить ее график

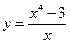
5. Вычислить неопределенный интеграл

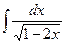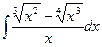1) ; 2) ; 3) .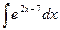

6. Вычислить определенный интеграл

1) 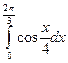; 2) 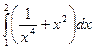; 3) Вычислить площадь фигуры, ограниченной графиками функций , .

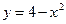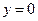7. Даны числа , , ,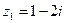

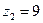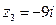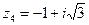
1. Изобразить на числовой плоскости

2. Найти модули и аргументы чисел 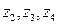. Записать 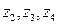в тригонометрической форме.

3. Вычислить , , .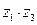

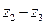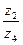Вариант 10

1. Решить систему уравнений по формулам Крамера

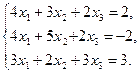
Вычислить пределы функций

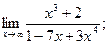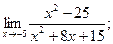1) 2) 3)

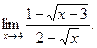
3. Вычислить производные функций

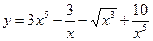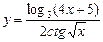1) ; 2) ; 3) .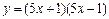

4. Провести полное исследование функции и построить ее график

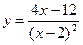
5. Вычислить неопределенный интеграл

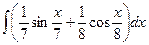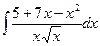1) ; 2) ; 3) .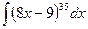

6. Вычислить определенный интеграл

1) 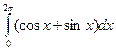; 2) 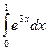; 3) Вычислить площадь фигуры, ограниченной графиками функций , .

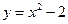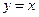7. Даны числа , , ,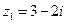

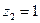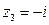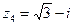
1. Изобразить на числовой плоскости

2. Найти модули и аргументы чисел 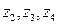. Записать 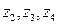в тригонометрической форме.

3. Вычислить , , .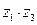

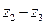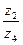ВОПРОСЫ ДЛЯ ПОДГОТОВКИ К ДИФФЕРЕНЦИРОВАННОМУ ЗАЧЕТУ ПО ДИСЦИПЛИНЕ «МАТЕМАТИКА»

14. Матрицы. Виды матриц.

15. Действия над матрицами.

16. Определители 1-го, 2-го порядков.

17. Определители 3-го порядка. Правило треугольников.

18. Система линейных алгебраических уравнений. Формулы Крамера.

19. Предел функции в точке. Основные теоремы о пределах.

20. Предел функции при x стремящемся к бесконечности. Замечательные пределы.

21. Непрерывность функции в точке и на промежутке. Свойства непрерывных функций.

22. Точки разрыва функции. Классификация точек разрыва.

23. Производная функции.

24. Геометрический смысл производной.

25. Механический смысл производной.

26. Таблица производных.

27. Понятие сложной функции. Производная сложной функции.

28. Схема исследования функции. Область определения функции. Четность и нечетность функции. Нули функции. Возрастание и убывание функции, правило нахождения промежутков монотонности. Точки экстремума функции, правило нахождения экстремумов функции.

29. Асимптоты функции.

30. Первообразная. Свойства первообразной.

31. Неопределенный интеграл. Основные свойства неопределенного интеграла.

32. Таблица неопределенных интегралов.

33. Методы интегрирования: метод непосредственного интегрирования; метод замены переменной (метод подстановки).

34. Определенный интеграл. Понятие интегральной суммы.

35. Основные свойства определенного интеграла.

36. Геометрический смысл определенного интеграла.

37. Методы вычисления определенных интегралов. Формула Ньютона-Лейбница.

38. Геометрические и физические приложения определенного интеграла.

39. Комплексные числа. Алгебраическая и геометрическая записи комплексного числа.

40. Действия над комплексными числами.

41. Понятие события. Достоверные, невозможные, совместные, несовместные, противоположные события. Классическое определение вероятности.

42. Теорема сложения вероятностей. Теорема умножения вероятностей.

43. Случайная величина. Дискретная и непрерывная случайные величины.

44. Закон распределения дискретной случайной величины.

45. Математическое ожидание дискретной случайной величины. Отклонение случайной величины. Дисперсия дискретной случайной величины. Среднее квадратичное отклонение случайной величины.

46. Логические операции: отрицание, дизъюнкция, конъюнкция, строгая конъюнкция, импликация, эквиваленция.

47. Булевы функции.

Дифференцированный зачет проводится в форме тестирования.

Приложение 1

Сургутский филиал Финуниверситета

КОНТРОЛЬНАЯ РАБОТА

по дисциплине «Математика»

Выполнил: студент (ка) __ курса ___ группы Иванов И.И. Проверил: преподаватель Юдина О.Г.   Дата проверки:   «____»_____________20___   ________________________ (подпись преподавателя)

Сургут 201_