Зависимость крутящего момента от частоты вращения коленчатого вала

Опытные данные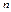
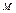Расчетные данные		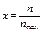0,25	0,375	0,500	0,625	0,750	0,875	1,0
	0,0625	0,1406	0,2500	0,3906	0,5625	0,7656	1,0
	394,7	408,3		405,64	389,35	363,1	326,89
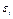	-4,7	1,7	3,0	-0,64	0,65	6,9	3,11

Р е ш е н и е. Из опытов предшествующих исследований известно, что зависимость 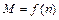описывается следующей функцией

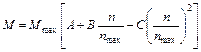, (79)

где 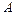, , 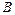- опытные коэффициенты, зависящие от типа двигателя; - крутящий момент при максимальной частоте вращения коленчатого вала .

Будем искать эмпирическую формулу в виде квадратичной зависимости

, (80)

где 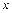- отношение текущей частоты вращения коленчатого вала 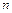к .

Для определения коэффициентов 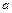, , 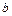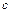применим метод средних. Подставляя опытные данные в формулу (80), получаем выражения для отклонений

;

;

;

;

;

;

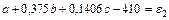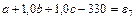. (81)

Отклонения 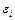(81) разобьем на три группы, получив 3 системы уравнений. В первую систему входят уравнения с отклонениями 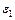, , , 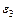во вторую - , 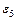и в третью - 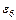, . Почленно сложим уравнения в каждой системе (группе), предварительно сделав допущение, что отклонения равны нулю. Таким образом получим систему трех уравнений

;

;

. (82)

Решая систему (82), находим 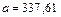; ; . Следовательно, эмпирическая формула, описывающая зависимость крутящего момента от частоты коленчатого вала двигателя внутреннего сгорания имеет вид

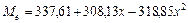. (83)

Сумма квадратов отклонений равна .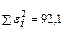

7.3. Точечный метод наименьших квадратов

Наилучшие результаты при определении коэффициентов эмпирической формулы дает метод наименьших квадратов. Суть метода заключается в том, что если все измерения функции ,…, равноточные и распределение ошибок измерений соответствует нормальному закону, то параметры исследуемого уравнения определяются из условия минимума суммы квадратов отклонений измеренных значений функции 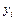от расчетных , т.е.

. (84)

Значения неизвестных коэффициентов формулы, которые обеспечивают минимизацию суммы (84), находят по правилам дифференциального исчисления. Обычно находят частные производные по искомым коэффициентам от выражения типа (84), приравнивают их к нулю и решают полученную систему уравнений относительно неизвестных коэффициентов аппроксимирующей функции.

Для линейной функции (все аппроксимирующие функции можно привести к линейной)

, (85)

подставляя в (84) вместо ее аналитическое выражение (85), будем иметь

. (86)

Найдем частные производные по параметрам 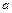и и приравняем их к нулю.

;

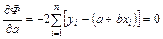. (87)

Из (87) получим, так называемую, нормальную систему уравнений

,

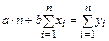, (88)

решая которую находятся неизвестные коэффициенты

; , (89)

где , , 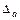- определители системы (88).

;

;

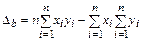. (90)

Здесь суммирование ведется по всем 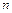экспериментальным точкам.

Для составления системы нормальных уравнений можно использовать следующий формальный прием, суть которого покажем на примере полинома второй степени

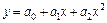. (91)

Полагая 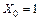, , 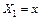, приведем (91) к виду

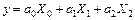. (92)

Система нормальных уравнений для (92), из решения которой находятся коэффициенты 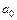, 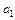и имеет вид

;

;

, (93)

где 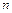- количество экспериментальных точек .

Принцип составления системы нормальных уравнений сводится к следующему формальному приему. Для получения левой части первого уравнения системы (93) необходимо просуммировать по всем опытам произведения значений фиктивного фактора поочередно на значения факторов , , 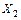. Для получения второго уравнения суммируются произведений фактора на факторы , , 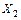. Третье уравнение получается суммированием произведения фактора 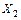на факторы , , 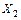. Правые части уравнений состоят из суммы произведений значений факторов , , 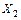на значения величины .

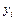П р и м е р 11. Зависимость мощности от частоты вращения коленчатого вала 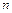двигателя при испытании его по скоростной характеристике представлена в таблице 13. Составить эмпирическую формулу для зависимости .

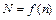Таблица 13