Приведение дифференциальных уравнений к канонической форме и определение начальных условий

На рис. 4.2 показана взаимосвязь переменных разных элементов модели.

СГ

Нагрузка

АРН

U

I

КН

U

I

Iу

If

МРЧВ

Мэ

ПД

ω

μр

Рис. 4.2.

Для численного решения дифференциальных уравнений они должны быть приведены к канонической форме. Как следует из рис. 4.2, решение этой задачи для части модели, содержащей СГ, АРН, КН и нагрузку, («электрическая» часть) отличается от части с ПД и МРЧВ («механической» части).

Приведение уравнений «электрической» части к канонической форме:

- приравниваются соответствующие составляющие напряжения СГ и статической нагрузки ((4.1)=(4.17), (4.2)=(4.18)), а также СГ и АРН – ((4.3)=(4.12));

- производится подстановка составляющих потокосцеплений ((4.6)…(4.10)) и 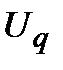из (4.18) в полученные равенства и в уравнения (4.4) и (4.5);

- в левой части уравнений группируются члены, содержащие производные токов, а в правой – свободные члены.

В результате будет получена система из пяти дифференциальных уравнений следующего вида:

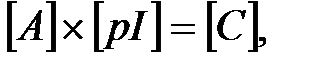(4.19)

где

.

Для приведения системы уравнений (4.19) к канонической форме необходимо разрешить ее относительно производных:

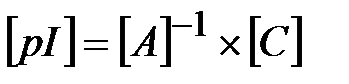. (4.20)

Таким образом, совокупность дифференциальных уравнений (4.20) и дифференциального уравнения (4.13), описывают процессы в «электрической» части модели.

Приведение уравнений «механической» части к канонической форме:

В систему дифференциальных уравнений ПД входит уравнение 2-го порядка (4.16), описывающее действие МРЧВ. Понижение порядка дифференциального уравнения производится традиционным способом – введением вспомогательной переменной. Так, если в качестве вспомогательной переменной взять h, то система уравнений ПД с МРЧВ примет следующий вид:

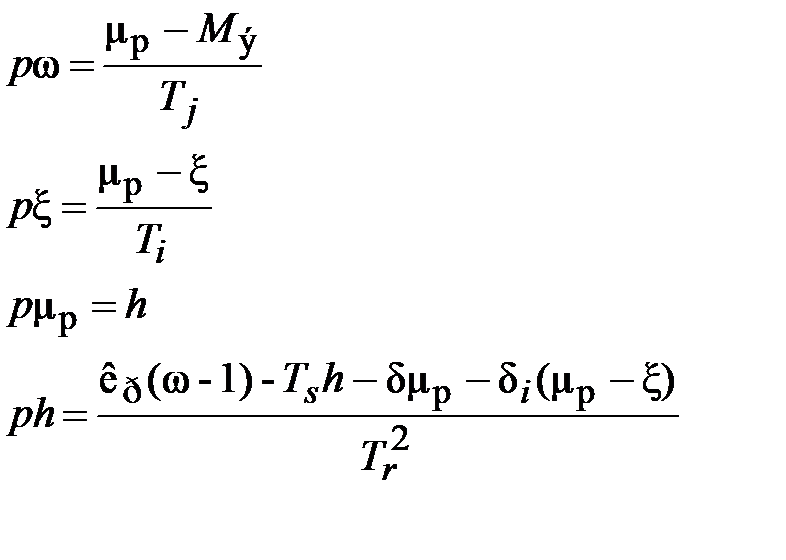. (4.21)

В рассматриваемой математической модели ГА необходимо учесть следующие ограничения: .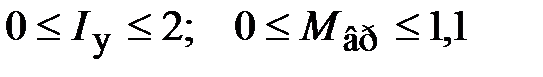

Для численного решения дифференциальных уравнений (2.41) и (2.37) применяются стандартные методы: Эйлера – Коши, Рунге – Кутта, Рунге – Кутта – Мерсона, Рунге – Кутта – Фельберга и др.

Применение любого из этих методов требует определения начальных значений переменных (начальных условий). Начальные условия определяются из исходной системы уравнений (4.1…4.16) с учетом особенностей предшествующего режима.

Непосредственно из особенностей холостого хода следует:

;

.

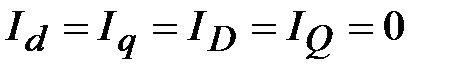Для определения 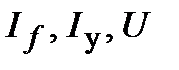положим производные всех переменных равными нулю, что соответствует установившемуся режиму. В результате получим:

;

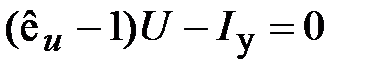; (4.22)

. (4.23)

Решая совместно уравнения (4.22) и (4.23), находим недостающие начальные значения переменных:

;

.

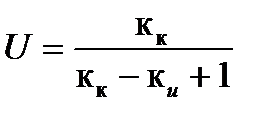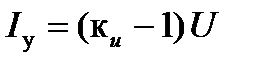Данные для СГ, выбранного в 1-ой работе, берутся из табл. П1. Параметры регуляторов представлены в табл. П2.

Пример программной реализации в пакете Matlab и вид представляемой информации

В приводимом примере исследуется процесс наброса нагрузки и анализируется максимальные отклонения напряжения.

Программная реализация включает в себя пять файлов c расширением «m»:

1.В файле Prac_4.m:

· определяется множество значений отклонения напряжения при всех сочетаниях 6 значений нагрузки 6 значений коэффициента мощности;

· определяются c помощью оператора «polyfit» 6 полиномов 5 степени и 6 полиномов 3 степени вида: ΔU_min=f(cosφ), при I_n=const, и такое же количество – ΔU_min=f(I), при cosφ_n=const, где n=1…6;

· определяются значения отклонения напряжения по полученным полиномам для исходных данных с помощью оператора «polyval»;

· осуществляется сравнение значений отклонений напряжения, полученных на основе математической модели и полиномов, по результатам сравнения выбирается степень полинома;

· формируется графическое представление полученных полиномиальных зависимостей;

· с помощью оператора «save» создается файл данных poldu.mat, используемый в других файлах.

Вид информации, представляемой по результатам выполнения файла:

1. Кривые изменения U для cosφ, последовательно принимающего значения:0 0,2 0,4 0,6 0,8 1,0, (рис 4.3); ω для таких же условий (рис. 4.4) и переменных математической модели для cosφ=0,8 (рис. 4.5) при набросе номинальной нагрузки.

2. Значения отклонения напряжения (табл. 4.2).

Таблица 4.2

Нагрузка, о.е.	Отклонение напряжения, %, при следующих значениях коэффициента мощности (cosφ)
	0,2	0,4	0,6	0,8	1,0
0,1	5,5	2,7	1,8	1,5	1,1	0,1
0,2	10,6	5,6	4,0	3,2	2,4	0,4
0,4	19,0	10,9	8,0	6,4	4,7	0,2
0,5	22,4	13,3	9,9	7,9	5,8	-0,1
0,8	31,3	19,8	15,2	12,1	8,9	-1,2
1,0	35,6	23,6	18,5	14,9	10,9	0,1

В представленных данных провал напряжения имеет знак «+», превышение – «-».

Рис. 4.3

Рис. 4.4

Рис. 4.5

3. Совокупности полиномов:

· 1-го вида ΔU_min=f(cosφ), при I_n=const (табл. 4.3):

Таблица 4.3

Нагрузка, %	Полиномы
5-ой степени
0,1	ΔUmin=-30,3953(cosφ)5+87,2125(cosφ)4-104,5607(cosφ)3+65,9469(cosφ)2-23,5276(cosφ) +5,4715
0,2	ΔUmin=-50,4019(cosφ)5+142,2689(cosφ)4-171,3676(cosφ)3+110,6125(cosφ)2-41,3199(cosφ)+10,6381
0,4	ΔUmin=-109,2913(cosφ)5+286,7041(cosφ)4-316,0632(cosφ)3+187,3897(cosφ)2-67,5573(cosφ)+19,0390
0,5	ΔUmin=-132,1801(cosφ)5+338,2267(cosφ)4-363,7093(cosφ)3+211,1021(cosφ)2-75,9210(cosφ)+22,4156
0,8	ΔUmin=-227,2099(cosφ)5+551,1781(cosφ)4-546,3974(cosφ)3+287,1136(cosφ)2-97,1023(cosφ)+31,2532
1,0	ΔUmin=-206,1761(cosφ)5+501,7216(cosφ)4-506,8194(cosφ)3+273,6460(cosφ)2-97,8407(cosφ)+35,5661
3-ей степени
0,1	ΔUmin=-15,9180(cosφ)3+28,8540(cosφ)2-18,2510(cosφ)+5,4361
0,2	ΔUmin=-29,0750(cosφ)3+51,9893(cosφ)2-33,1068(cosφ)+10,5858
0,4	ΔUmin=-51,0992(cosφ)3+87,0435(cosφ)2-54,7290(cosφ)+18,9854
0,5	ΔUmin=-60,2975(cosφ)3+100,2101(cosφ)2-62,3539(cosφ)+22,3741
0,8	ΔUmin=-85,2780(cosφ)3+133,6166(cosφ)2-80,6873(cosφ)+31,2648
1,0	ΔUmin=-85,2508(cosφ)3+132,4319(cosφ)2-82,5868(cosφ)+35,5723

· 2-го вида ΔU_min=f(I), при cosφ_n=const (табл. 4.4):

Таблица 4.4

cosφ	Полиномы 5-ой степени
	ΔUmin=-75,6348 I5+174,0991 I4-125,2196 I3+6,2401 I2+56,1819 I-0,1005
0,2	ΔUmin=-24,6429 I5+60,6236 I4-48,5908 I3+6,5376 I2+30,0267 I-0,3281
0,4	ΔUmin=-18,5867 I5+48,5478 I4-43,8452 I3+12,8175 I2+19,8041 I-0,2279
0,6	ΔUmin=4,9985 I5-12,3939 I4+13,2316 I3-9,9762 I2+19,4383 I-0,4062
0,8	ΔUmin=-2,6808 I5+4,2968 I4+1,6542 I3-7,0776 I2+15,0410 I-0,3527
1,0	ΔUmin=57,5719 I5-129,7957 I4+118,1457 I3-59,1112 I2+14,0604 I-0,7734

4. Результаты выбора степени полиномов на основании сравнения значений отклонения напряжения, рассчитанных по исходным данным с помощью математической модели (табл. 4.2) и полиномов (табл. 4.5 и 4.6):

· значения отклонения напряжения, полученные по полиномам 1-го вида (табл. 4.3):

Таблица 4.5

Нагрузка, о.е.	Отклонение напряжения, %, при следующих значениях коэффициента мощности (cosφ)
	0,2	0,4	0,6	0,8	1,0
По полиномам 5-ой степени
0,1	5,5	2,7	1,8	1,5	1,1	0,1
0,2	10,6	5,6	4,0	3,2	2,4	0,4
0,4	19,0	10,9	8,0	6,4	4,7	0,2
0,5	22,4	13,3	9,9	7,9	5,8	-0,1
0,8	31,3	19,8	15,2	12,1	8,9	-1,2
1,0	35,6	23,6	18,5	14,9	10,9	0,1
По полиномам 3-ей степени
0,1	5,4	2,8	1,7	1,5	1,2	0,1
0,2	10,6	5,8	3,8	3,2	2,5	0,4
0,4	19,0	11,1	7,8	6,4	4,7	0,2
0,5	22,4	13,4	9,6	8,0	5,8	-0,1
0,8	31,3	19,8	14,9	12,5	8,6	-1,1
1,0	35,6	23,7	18,3	15,3	10,6	0,2

· значения отклонения напряжения, полученные по полиномам 2-го вида (табл. 4.4):

Таблица 4.6

cosφ	Отклонение напряжения, %, при следующих значениях нагрузки,о.е.
0,1	0,2	0,4	0,5	0,8	1,0
0,0	5,5	10,6	19,0	22,4	31,3	35,6
0,2	2,7	5,6	10,9	13,3	19,8	23,6
0,4	1,8	4,0	8,0	9,9	15,2	18,5
0,6	1,5	3,2	6,4	7,9	12,1	14,9
0,8	1,1	2,4	4,7	5,8	8,9	10,9
1,0	0,1	0,4	0,2	-0,1	-1,2	0,1

Вывод: значения отклонений напряжения, полученные по полиномам 5-ой степени, полностью совпадают с результатами математической модели.

5. Графическое представление:

· полиномиальных зависимостей 1-го вида (табл. 4.3) представлено на рис. 4.6:

Рис. 4.6

· полиномиальных зависимостей 2-го вида (табл. 4.4) представлено на рис. 4.7:

Рис. 4.7

2.Файл vspuga.mвызываетсяиз файлов Prac_4.m и Prov_P4.m оператором «[t,y]=ode45('vspuga',[0 1.5],y0)». Он содержажит информацию о методе решения дифференциальных уравнений (ode45 – Рунге-Кутта 4..5 порядков), о диапазоне времени (время начала расчета, время конца расчета) – [0 1.5], и начальных условиях, формируемых в виде массива y0. В нем находятся дифференциальные уравнения, разрешенные относительно производных. Он начинается с function pry=vspuga(t,y), где pry – массив производных.

3.Файл Opr_hpr4.m.Вэтом файле решается задача определения отклонения напряжения по полиномиальным зависимостям, полученным в файле Prac_4.m, для произвольных значений I_зад и cosφ_зад. Он начинается с загрузки с помощью оператора «load» файла данных poldu.mat,содержащим полиномы и исходные данные.

Реализованный в примере алгоритм базируется на полиномах 5-ой степени 2-х видов табл. 4.3 и 4.4. Условно его можно разбить на 2-е части: расчет отклонения напряжения по полиномам и выбор из полученных 2-х результатов наиболее близкого к значению, получаемому на математической модели.

Основной задачей первой части является поиск расчетного полинома по I из совокупности полиномов 1-го вида и по cosφ – 2-го вида. Поиск осуществляется на основе следующих проверок:

· если I_зад= I или (и) cosφ_зад=cosφ, то при подстановке в соответствующий этим параметрам полином 1-го вида cosφ_зад или (и) I_зад – 2-го будут получены значения отклонения напряжения;

· если I_зад≠ I или (и) cosφ_зад≠cosφ, то для расчета по полиномам 1-го вида предлагается брать ближайший в направлении увеличения нагрузки, а для полиномов 2-го вида – ближайший в направлении уменьшения коэффициента мощности.

После получения 2-х значений отклонений U необходимо перейти ко 2-ой части алгоритма. В примере для выбора одного из двух значений отклонений U использовался следующий алгоритм: преимущество имеет значение, полученное по полиному, выбранному по условию I_зад= I или (и) cosφ_зад=cosφ, если это условие не выполняется, то выбирается меньшее значение.

Для проверки правильности алгоритма, по рекомендациям табл.4.1 были выбраны значения I_зад и cosφ_зад. Выбранные значения, а также результаты расчета отклонений U, полученные с помощью полиномов 2-х видов и математической модели (Prov_P4.m), представлены в табл. 4.7.

Таблица 4.7

Параметры	№ опыта
Нагрузка, о.е.	0,5	0,3	0,7	0,8
Коэффициент мощности	0,7	0,6	0,3	0,8
ΔU по математической модели	6.9620	4.7938	15.3183	8.8789
ΔU по полиному 1-го вида	6.9147	6.3537	17.1087	8.8789
ΔU по полиному 2-го вида	7.8544	4.7964	17.6413	8.8789

В табл.4.7 выделены параметры, совпадающие с исходными данными.

Полученные данные подтверждают правильность разработанного алгоритма.

Вид информации, представляемой по результатам выполнения файла:

Необходимо представить алгоритм и результаты расчета для 4-х точек в форме табл. 4.7.

4.Файл Gr_pr4.mреализует решение задачи нахождения границы между областями с допустим (ΔU≤15%) и недопустимым (ΔU>15%) значениями отклонения напряжения в полиномиальной форме cosφ=f(I). Алгоритм включает в себя решение следующих задач:

· нахождение значений cosφ, при заданных значениях I, которые являются положительными вещественными корнями полиномиальных зависимостей 1-го вида, приравненных к 15, и определяются с помощью оператора «roots»;

· нахождение значений I, при заданных значениях cosφ, которые являются положительными вещественными корнями полиномиальных зависимостей 2-го вида, приравненных к 15, и определяются с помощью оператора «roots»;

· объединение и сортировка полученных множеств значений cosφ и I, характеризующих координаты границы;

· определение отклонений U по математической модели (Prov_P4.m) в точках, определяющих координаты границы;

· получение на множествах cosφ и I полиномиальной зависимости границы вида cosφ=f(I) с помощью оператора «polyfit»;

Вид информации, представляемой по результатам выполнения файла:

· значения полученных координат границы и отклонений напряжения в них, полученные с помощью математической модели (табл. 4.8);

Таблица 4.8

I, о.е.	0.2962	0.4000	0.5000	0.5778	0.7906	0.8000	1.0000
cosφ		0.0734	0.1421	0.2000	0.4000	0.4095	0.5936
ΔU, %	14.9710	15.0413	14.9910	15.0195	15.0121	15.0002	15.0002

· полином:

cosφ=-2,9767 I⁵+6,0835 I⁴-3,2936 I³-0,0798 I²+1,1475 I-0,2873

· графическое представление полиномиальной зависимости (рис. 4.8):

Рис. 4.8

· проверка правильности определения выполнения условия ΔU≤15%, которая проводится с помощью файла Prov_P4.mдля произвольно заданного значения I и 2-х значений cosφ, находящихся выше и ниже полученной границы. В примере проверка была проведена для I=0,6 и cosφ=0,2 и cosφ=0,3. В результате были получены следующие значения: ΔU=15,5324 и ΔU=13,3049, которые показали правильность координатполученной границы.

5.Файл Prov_P4.mпредназначен для реализации проверок по математической модели. Он работает совместно с файлом vspuga.m.Допускается функции проверки предусмотреть в файле Prac_4.m.

Программные реализации приведены в Приложении 3.