Парная регрессия и корреляция.

ЭКОНОМЕТРИКА

Методические указания

по выполнению контрольной работы

для студентов заочной формы обучения

Казань

Введение

Моделирование экономических процессов сопряжено с рядом трудно­стей. Это и многообразие экономической жизни и конфликт интересов различных соци­альных групп и внешний фактор в силу открытости современной экономики. Возникает определенный пессимизм по отношению к возможностям и полез­ности количественного моделирования, стремление к качественному описанию взаимосвязей экономических величин. Тем не менее, конкретные решения, влекущие ма­териальную ответственность, не могут опираться на качественные рассуждения и требуют точных вычислений. Востребованные практикой средства анализа данных, на которые можно опираться в процессе принятия решений, предоставляет эконометрика. В этой науке соединились возможности экономической теории и математики.

Данные методические указания вклю­чают теоретические выкладки, пример решения эконометрической задачи и задания к контрольной работе. В конце методических указаний приведен пример оформления контрольной работы и правила выбора варианта. Уровень сложности предлагаемых заданий и относительно небольшое количество наблюдений по­зволяют выполнить предлагаемую работу с помощью обычного калькулятора. Однако предполагается, что при выполнении работы студенты будут использовать оболочку Excel.

Выполнение работы следует начинать с проработки методических указаний, парал­лельно изучая теорию в соответствии со стандартом и рабочей программой курса. Затем выполняются задания своего варианта.

Парная регрессия и корреляция.

Постановка задачи.

По имеющимся данным 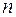наблюдений за совместным изменением двух параметров и необходимо определить аналитическую зависимость 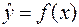, наилучшим образом описывающую данные наблюдений.

2.2 Понятие линейной регрессии.

Функция 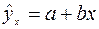, задающая среднее значение переменной , при условии, что независимая переменная приняла фиксированное значение, называется функцией (линейной) регрессии.

Оценка параметров модели.

Для оценки параметров линейной регрессии используется метод наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров, при которых сумма отклонений фактических значений результативного признака от теоретических значений 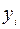при тех же значениях фактора 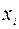минимальна, т.е.

.

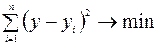В случае линейной регрессии параметры 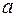и 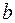находятся из следующей системы нормальных уравнений МНК:

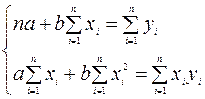
Можно воспользоваться готовыми формулами, которые вытекают из этой системы:

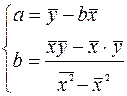
Оценка тесноты связи.

В качестве меры для тесноты линейной связи между переменными используется коэффициент корреляции. Приведем формулу выборочного коэффициента корреляции переменных и :

.

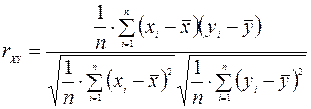Коэффициент корреляции будет положителен, если отклонения переменных и от своих средних значений, как правило, имеют одинаковый знак, и отрицательным – если разные знаки. Коэффициент корреляции является безразмерной величиной. Его величина меняется от -1 в случае строгой линейной отрицательной связи до +1 в случае строгой линейной положительной связи. Близкая к 0 величина коэффициента корреляции говорит об отсутствии линейной связи между переменными, но не об отсутствии связи между ними вообще.

Пример.

По 21 региону страны изучается зависимость розничной продажи телевизоров ( ) от среднедушевого денежного дохода в месяц ( ).

Номер региона	Среднедушевой денежный доход в месяц, тыс. руб.,	Объем розничной продажи телевизоров, тыс. шт.,
	2,4	21,3
	2,1
	2,6	23,3
	1,7	15,8
	2,5	21,9
	2,4
	2,6
	2,8	23,9
	2,6
	2,6	24,6
	2,5
	2,9
	2,6
	2,2
	2,6
	3,3	31,9
	3,9
		35,4
	3,7
	3,4

Необходимо найти зависимость, наилучшим образом отражающую связь между переменными и .

Рассмотрим вопрос применения модели линейной регрессии в этой задаче.

Построим поле корреляции, т.е. нанесем исходные данные на координатную плоскость. Для этого воспользуемся, например, возможностями MS Excel 2003.

Подготовим таблицу исходных данных.

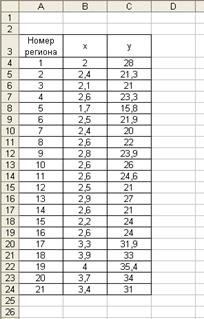
Нанесем на координатную плоскость исходные данные:

Характер расположения точек на графике дает нам основание предположить, что искомая функция регрессии линейная: 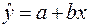. Для оценки коэффициентов уравнения регрессии необходимо составить и решить систему нормальных уравнений ( ).

По исходным данным рассчитываем необходимые суммы:

Номер региона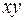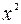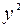
	2,4	21,3	51,12	5,76	453,69
	2,1		44,1	4,41
	2,6	23,3	60,58	6,76	542,89
	1,7	15,8	26,86	2,89	249,64
	2,5	21,9	54,75	6,25	479,61
	2,4			5,76
	2,6		57,2	6,76
	2,8	23,9	66,92	7,84	571,21
	2,6		67,6	6,76
	2,6	24,6	63,96	6,76	605,16
	2,5		52,5	6,25
	2,9		78,3	8,41
	2,6		54,6	6,76
	2,2		52,8	4,84
	2,6		62,4	6,76
	3,3	31,9	105,27	10,89	1017,61
	3,9		128,7	15,21
		35,4	141,6		1253,16
	3,7		125,8	13,69
	3,4		105,4	11,56
Сумма	57,4	530,1	1504,46	164,32	13926,97

Составляем систему уравнений:

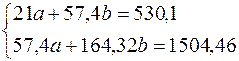
Имеем систему линейных алгебраических уравнений, которая может быть решена, например, по формулам Крамера. Для этого вычислим следующие определители:

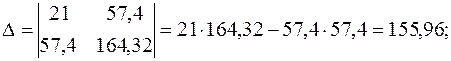
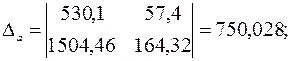
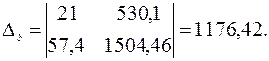
Тогда, согласно теореме Крамера,

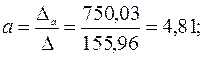
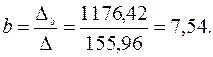
Получаем уравнение регрессии:

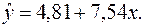
Величина коэффициента регрессии 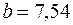означает, что увеличение среднедушевого месячного дохода на 1 тыс. руб. приведет к увеличение объема розничной продажи в среднем на 7 540 телевизоров. Коэффициент 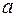в данном случае не имеет содержательной интерпретации.

Оценим тесноту линейной связи между переменными и качество построенной модели в целом.

Для оценки тесноты линейной зависимости рассчитаем коэффициент детерминации. Для этого необходимо провести ряд дополнительных вычислений.

Прежде всего, найдем выборочное среднее 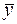по формуле:

.

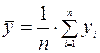Для рассматриваемого примера имеем:

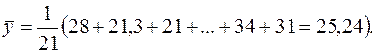
Теперь произведем расчет остальных вспомогательных величин:

Номер региона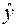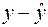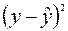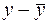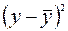
			19,76	8,24	67,89	2,76	7,60
	2,4	21,3	22,75	-1,45	2,11	-3,94	15,55
	2,1		20,51	0,49	0,24	-4,24	18,00
	2,6	23,3	24,25	-0,95	0,90	-1,94	3,77
	1,7	15,8	17,52	-1,72	2,95	-9,44	89,17
	2,5	21,9	23,50	-1,60	2,56	-3,34	11,17
	2,4		22,75	-2,75	7,57	-5,24	27,49
	2,6		24,25	-2,25	5,04	-3,24	10,52
	2,8	23,9	25,74	-1,84	3,39	-1,34	1,80
	2,6		24,25	1,75	3,08	0,76	0,57
	2,6	24,6	24,25	0,35	0,13	-0,64	0,41
	2,5		23,50	-2,50	6,24	-4,24	18,00
	2,9		26,49	0,51	0,26	1,76	3,09
	2,6		24,25	-3,25	10,54	-4,24	18,00
	2,2		21,26	2,74	7,53	-1,24	1,54
	2,6		24,25	-0,25	0,06	-1,24	1,54
	3,3	31,9	29,48	2,42	5,86	6,66	44,32
	3,9		33,96	-0,96	0,93	7,76	60,17
		35,4	34,71	0,69	0,47	10,16	103,17
	3,7		32,47	1,53	2,34	8,76	76,69
	3,4		30,23	0,77	0,60	5,76	33,14
Сумма	57,4	530,1			130,68		545,73

Здесь столбец « 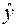» – это значения 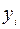, 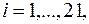рассчитанные с помощью построенного уравнения регрессии, столбцы « 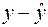» и 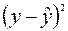– это столбцы, так называемых, «остатков»: разностей между исходными значениями 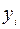, 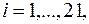и рассчитанными с помощью уравнения регрессии 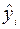, а также их квадратов, а в последних двух столбцах – разности между исходными значениями 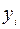, выборочным средним 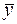, а также их квадраты.

Для вычисления коэффициента детерминации воспользуемся формулой ( ):

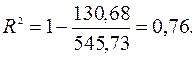
Значение коэффициента детерминации позволяет сделать предварительный вывод о том, что у нас имеются основания использовать модель линейной регрессии в данной задаче, поскольку .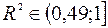

Построим линию регрессии на корреляционном поле, для чего добавим на координатной плоскости точки, соответствующие уравнению регрессии ( ).

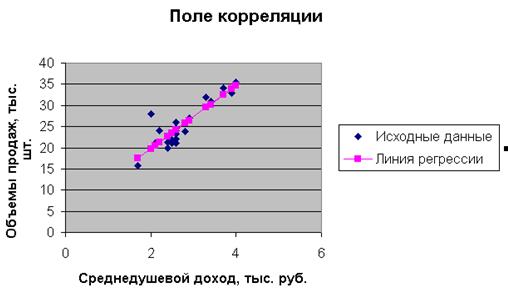
Нанесем теперь уравнение регрессии на диаграмму, используя специальные средства Excel. Для этого необходимо выделить правой кнопкой мыши исходные точки и выбрать опцию Добавить линию тренда.

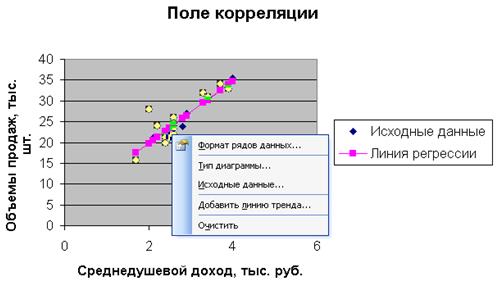
В открывшемся меню Параметры линии тренда выбрать Линейную аппроксимацию. Далее поставить флажок напротив полей Показывать уравнение на диаграмме и Поместить на диаграмму величину достоверности аппроксимации .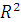

Нажав на ОК, получаем еще одну прямую на диаграмме, которая совпадает с построенными ранее точками линии регрессии:

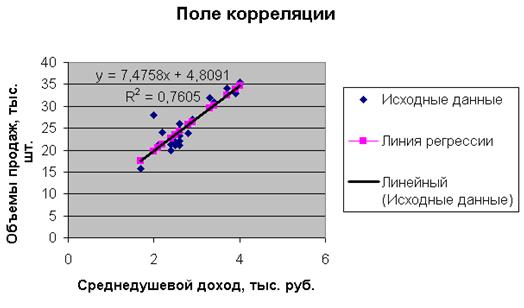
Сплошная черная линия на диаграмме – это линия регрессии, рассчитанная средствами Excel. Линия регрессии, построенная нами ранее, совпала с данной линией регрессии. Нетрудно убедиться, что уравнение регрессии и коэффициент детерминации тоже совпадают с полученными ранее вручную.

Найдем теперь среднюю ошибку аппроксимации для оценки погрешности модели. Для этого нам потребуется вычислить еще ряд промежуточных величин:

Номер региона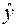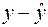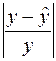
			19,76	8,24	0,29
	2,4	21,3	22,75	-1,45	0,07
	2,1		20,51	0,49	0,02
	2,6	23,3	24,25	-0,95	0,04
	1,7	15,8	17,52	-1,72	0,11
	2,5	21,9	23,50	-1,60	0,07
	2,4		22,75	-2,75	0,14
	2,6		24,25	-2,25	0,10
	2,8	23,9	25,74	-1,84	0,08
	2,6		24,25	1,75	0,07
	2,6	24,6	24,25	0,35	0,01
	2,5		23,50	-2,50	0,12
	2,9		26,49	0,51	0,02
	2,6		24,25	-3,25	0,15
	2,2		21,26	2,74	0,11
	2,6		24,25	-0,25	0,01
	3,3	31,9	29,48	2,42	0,08
	3,9		33,96	-0,97	0,03
		35,4	34,71	0,69	0,02
	3,7		32,47	1,53	0,05
	3,4		30,23	0,77	0,02

Здесь столбец « 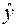» – это значения 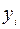, 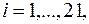рассчитанные с помощью построенного уравнения регрессии, столбец « 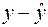» – это столбец так называемых «остатков»: разностей между исходными значениями 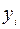, и рассчитанными с помощью уравнения регрессии 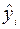, 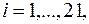и, наконец, последний столбец « 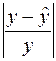» – это вспомогательный столбец для вычисления элементов суммы по формуле ( ). Просуммируем теперь элементы последнего столбца и разделим полученную сумму на 21 – общее количество исходных данных:

.

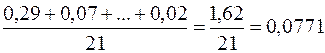Переведем это число в проценты и запишем окончательное выражение для средней ошибки аппроксимации:

.

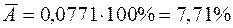Итак, средняя ошибка аппроксимации оказалась около 8%, что говорит о небольшой погрешности построенной модели. Данную модель, с учетом неплохих характеристик ее качества, вполне можно использовать для прогноза – одной из основных целей эконометрического анализа. Предположим, что среднедушевой месячный доход в одном из регионов составит 4,1 тыс. руб. Оценим, каков будет уровень продаж телевизоров в этом регионе согласно построенной модели? Для этого необходимо выбранное значение фактора подставить в уравнение регрессии ( ):

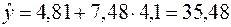(тыс. руб.),

т.е. при таком уровне дохода, розничная продажа телевизоров составит, в среднем, 35 480 телевизоров.

Приложение 1. Варианты заданий.

Вариант №1 (студенты фамилия которых начинается на А)

В таблице представлены статистические данные о размере товарооборота Х и суммы издержек обращения Y по десяти магазинам.

Товарооборот Х
Издержки обращения Y

Вариант №2 (студенты фамилия которых начинается на Б, В)

Образцы некоторого сплава были изготовлены при различных температурах, после чего была измерена прочность каждого образца. Обозначим через Х температуру изготовления сплава, через Y – величину прочности образца. В таблице приведены результаты измерений.

Х	0,5	1,0	1,5	2,0	2,5	3,0	3,5	4,0	4,5	5,0
Y

Вариант №3 (студенты фамилия которых начинается на Г, Д)

Обозначим через Х цену оптовой продажи некоторого товара, через Y—цену его розничной продажи.

Х

Y

Вариант №4 (студенты фамилия которых начинается на З, К)

Таблица содержит данные о росте (Х) и массе (Y) 25 выбранных наугад студентов.

Х

Y

Вариант №5 (студенты фамилия которых начинается на М, Н)

Х	6,7	6,9	7,2	7,3	8,4	8,8	9,1	9,8	10,6	10,7	11,1	11,8	12,1	12,4
Y	2,8	2,2	3,0	3,5	3,2	3,7	4,0	4,8	6,0	5,4	5,2	5,4	6,0	9,0

Приведены данные о годовой производительности труда в расчете на одного рабочего (Y) и энерговооруженности труда (Х) на предприятиях одной отрасли.

Вариант №6 (студенты фамилия которых начинается на П, Р)

На 10 территориях были измерены процентный показатель перенаселенности (Х) и показатель детской смертности (Y).

Х
Y

Вариант №7 (студенты фамилия которых начинается на С, Т)

Х	1,47	1,25	1,82	1,45	1,75	1,37	1,61	1,93	1,68	1,66
Y	34,08	35,89	36,93	32,31	34,91	30,20	31,23	48,13	30,08	42,86

Имеются данные о фондоотдаче оборудования (Х) и удельном весе продукции высшей категории качества (Y):

Вариант №8 (студенты фамилия которых начинается на Х, Ч)

В таблице содержатся данные, показывающие связь между количеством дней (Х), проведенных пациентами в больнице, и затратами больницы (Y), которые компенсируются страховой компанией.

Х

Y

Приложение 2. Образец оформления контрольной работы.

Государственное образовательное учреждение высшего профессионального образования

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ»

ПРЕПОДАВАТЕЛЬ

должность, уч. степень, звание		подпись, дата		инициалы, фамилия

КОНТРОЛЬНАЯ РАБОТА

по дисциплине: эконометрика

РАБОТУ ВЫПОЛНИЛА

СТУДЕНТ(КА) ГР.
			подпись, дата		инициалы, фамилия

Санкт-Петербург
2010

Задача.

По 21 региону страны изучается зависимость розничной продажи телевизоров ( 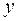) от среднедушевого денежного дохода в месяц ( ).

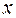Номер региона	Среднедушевой денежный доход в месяц, тыс. руб.,	Объем розничной продажи телевизоров, тыс. шт.,
	2,4	21,3
	2,1
	2,6	23,3
	1,7	15,8
	2,5	21,9
	2,4
	2,6
	2,8	23,9
	2,6
	2,6	24,6
	2,5
	2,9
	2,6
	2,2
	2,6
	3,3	31,9
	3,9
		35,4
	3,7
	3,4

Решение.

1. Построим поле корреляции.

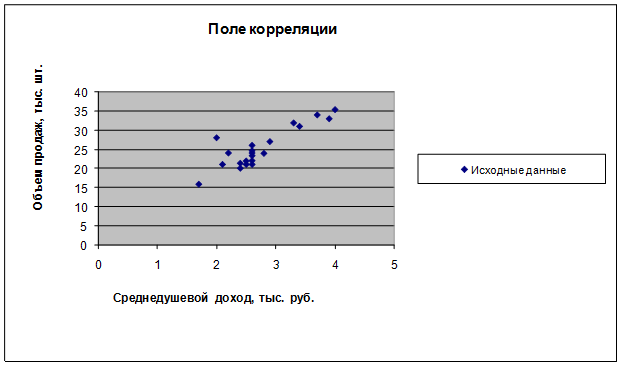
Расположение точек на диаграмме дает нам право предположить, что переменные связаны линейной зависимостью. Рассчитаем выборочные коэффициенты корреляции. Для этого проведем промежуточные вычисления, по формулам ( ) и поместим результаты вычислений в таблицу:

Номер региона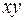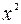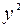
	2,4	21,3	51,12	5,76	453,69
	2,1		44,1	4,41
	2,6	23,3	60,58	6,76	542,89
	1,7	15,8	26,86	2,89	249,64
	2,5	21,9	54,75	6,25	479,61
	2,4			5,76
	2,6		57,2	6,76
	2,8	23,9	66,92	7,84	571,21
	2,6		67,6	6,76
	2,6	24,6	63,96	6,76	605,16
	2,5		52,5	6,25
	2,9		78,3	8,41
	2,6		54,6	6,76
	2,2		52,8	4,84
	2,6		62,4	6,76
	3,3	31,9	105,27	10,89	1017,61
	3,9		128,7	15,21
		35,4	141,6		1253,16
	3,7		125,8	13,69
	3,4		105,4	11,56
Сумма	57,4	530,1	1504,46	164,32	13926,97

Составляем систему уравнений:

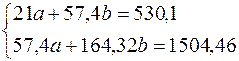
и решаем ее по формулам Крамера:

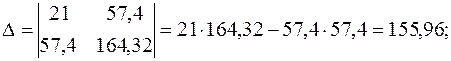
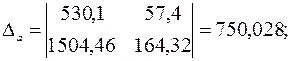
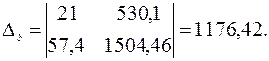
Тогда, согласно теореме Крамера,

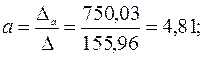
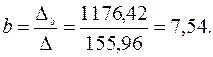
2. Получаем уравнение регрессии:

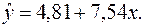
Величина коэффициента регрессии 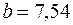означает, что увеличение среднедушевого месячного дохода на 1 тыс. руб. приведет к увеличение объема розничной продажи в среднем на 7 540 телевизоров. Коэффициент 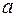в данном случае не имеет содержательной интерпретации.

3. Нанесем построенную линию регрессии на диаграмму. Для этого рассчитаем значения 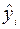, , 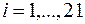по формуле:

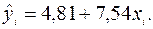
Результаты вычислений запишем в таблицу:

Номер региона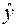
			19,76
	2,4	21,3	22,75
	2,1		20,51
	2,6	23,3	24,25
	1,7	15,8	17,52
	2,5	21,9	23,50
	2,4		22,75
	2,6		24,25
	2,8	23,9	25,74
	2,6		24,25
	2,6	24,6	24,25
	2,5		23,50
	2,9		26,49
	2,6		24,25
	2,2		21,26
	2,6		24,25
	3,3	31,9	29,48
	3,9		33,96
		35,4	34,71
	3,7		32,47
	3,4		30,23

Наносим на диаграмму точки из последнего столбца таблицы (Линия регрессии):

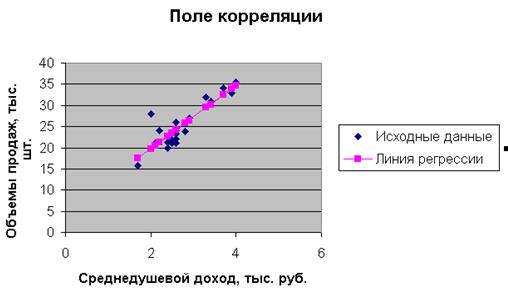
4. Для оценки тесноты линейной зависимости рассчитаем коэффициент детерминации. Для этого необходимо провести ряд дополнительных вычислений.

Прежде всего, найдем выборочное среднее 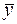по формуле:

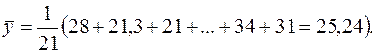
Теперь произведем расчет остальных вспомогательных величин:

Номер региона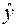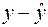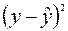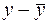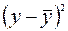
			19,76	8,24	67,89	2,76	7,60
	2,4	21,3	22,75	-1,45	2,11	-3,94	15,55
	2,1		20,51	0,49	0,24	-4,24	18,00
	2,6	23,3	24,25	-0,95	0,90	-1,94	3,77
	1,7	15,8	17,52	-1,72	2,95	-9,44	89,17
	2,5	21,9	23,50	-1,60	2,56	-3,34	11,17
	2,4		22,75	-2,75	7,57	-5,24	27,49
	2,6		24,25	-2,25	5,04	-3,24	10,52
	2,8	23,9	25,74	-1,84	3,39	-1,34	1,80
	2,6		24,25	1,75	3,08	0,76	0,57
	2,6	24,6	24,25	0,35	0,13	-0,64	0,41
	2,5		23,50	-2,50	6,24	-4,24	18,00
	2,9		26,49	0,51	0,26	1,76	3,09
	2,6		24,25	-3,25	10,54	-4,24	18,00
	2,2		21,26	2,74	7,53	-1,24	1,54
	2,6		24,25	-0,25	0,06	-1,24	1,54
	3,3	31,9	29,48	2,42	5,86	6,66	44,32
	3,9		33,96	-0,96	0,93	7,76	60,17
		35,4	34,71	0,69	0,47	10,16	103,17
	3,7		32,47	1,53	2,34	8,76	76,69
	3,4		30,23	0,77	0,60	5,76	33,14
Сумма	57,4	530,1			130,68		545,73

Для вычисления коэффициента детерминации воспользуемся формулой ( ):

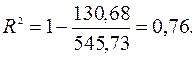
Значение коэффициента детерминации позволяет сделать предварительный вывод о том, что у нас имеются основания использовать модель линейной регрессии в данной задаче, поскольку .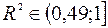

5. Нанесем теперь уравнение регрессии на диаграмму, используя специальные средства Excel («Добавить линию тренда»).

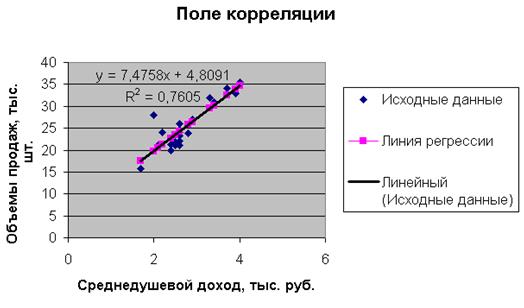
Линия регрессии, построенная нами ранее, совпала с данной линией регрессии. Нетрудно убедиться, что уравнение регрессии и коэффициент детерминации тоже совпадают с полученными ранее вручную.

6. Найдем теперь среднюю ошибку аппроксимации для оценки погрешности модели. Для этого нам потребуется вычислить еще ряд промежуточных величин:

Номер региона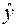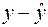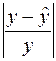
			19,76	8,24	0,29
	2,4	21,3	22,75	-1,45	0,07
	2,1		20,51	0,49	0,02
	2,6	23,3	24,25	-0,95	0,04
	1,7	15,8	17,52	-1,72	0,11
	2,5	21,9	23,50	-1,60	0,07
	2,4		22,75	-2,75	0,14
	2,6		24,25	-2,25	0,10
	2,8	23,9	25,74	-1,84	0,08
	2,6		24,25	1,75	0,07
	2,6	24,6	24,25	0,35	0,01
	2,5		23,50	-2,50	0,12
	2,9		26,49	0,51	0,02
	2,6		24,25	-3,25	0,15
	2,2		21,26	2,74	0,11
	2,6		24,25	-0,25	0,01
	3,3	31,9	29,48	2,42	0,08
	3,9		33,96	-0,97	0,03
		35,4	34,71	0,69	0,02
	3,7		32,47	1,53	0,05
	3,4		30,23	0,77	0,02

Просуммируем теперь элементы последнего столбца и разделим полученную сумму на 21 – общее количество исходных данных:

.

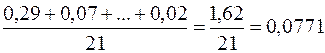Итак, средняя ошибка аппроксимации 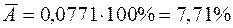. Величина ошибки оказалась около 8%, что говорит о небольшой погрешности построенной модели. Данную модель, с учетом неплохих характеристик ее качества, вполне можно использовать для прогноза – одной из основных целей эконометрического анализа.

7. Рассчитаем значение фактора, для которого необходимо построить прогноз. Для этого необходимо вычислить выборочное среднее значение по формуле:

.

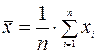Для нашей задачи среднее значение среднедушевого месячного дохода:

.

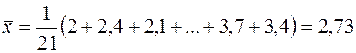Рассчитаем теперь значение .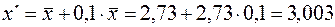

Подставим теперь полученное значение фактора 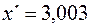в уравнение регрессии и найдем прогнозируемое значение:

.

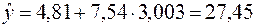Таким образом, если среднедушевой месячный доход в некотором регионе составит 3 003 руб., количество продаваемых телевизоров составит в среднем 27 450 шт. в месяц.

ЭКОНОМЕТРИКА

Методические указания

по выполнению контрольной работы

для студентов заочной формы обучения

Казань

Введение

Моделирование экономических процессов сопряжено с рядом трудно­стей. Это и многообразие экономической жизни и конфликт интересов различных соци­альных групп и внешний фактор в силу открытости современной экономики. Возникает определенный пессимизм по отношению к возможностям и полез­ности количественного моделирования, стремление к качественному описанию взаимосвязей экономических величин. Тем не менее, конкретные решения, влекущие ма­териальную ответственность, не могут опираться на качественные рассуждения и требуют точных вычислений. Востре