ЧАСТИЧНО – РЕКУРСИВНЫЕ ФУНКЦИИ
Глава 1
ЧАСТИЧНО – РЕКУРСИВНЫЕ ФУНКЦИИ
Свойства алгоритмов
Под алгоритмом решения задач некоторого класса обычно понимается общее правило, с помощью которого решение любой конкретной проблемы этого класса может быть найдено чисто механически и без всяких дополнительных размышлений о процессе решения. Среди известных примеров – алгоритм Евклида нахождения наибольшего общего делителя для двух натуральных чисел, алгоритм деления двух целых чисел, алгоритм перевода целого десятичного числа в двоичную систему счис- ления и т.п. Для любой задачи алгоритм ее решения должен быть доказан. Даже если на некотором наборе тестов соответствующая программа для ЭВМ выдала правиль- ный результат, принципиальное отсутствие доказательства правильности алгоритма может означать только одно: предлагаемый алгоритм решает какую–то другую за- дачу, возможно, являющуюся частным случаем поставленной задачи.
Слово "алгоритм" происходит от имени арабского математика Мохаммеда ибн Муса Альхваризми, который в IX столетии внес значительный вклад в разработку и практическое применение методов вычислений. Прогресс в развитии таких методов породил представление о том, что можно найти алгоритм решения любой поставлен- ной математической и даже философской проблемы. Вера в универсальность алго- ритмических методов была впервые подорвана работой Геделя, в которой была дока- зана алгоритмическая неразрешимость некоторых математических проблем. Точнее, было доказано, что известные математические проблемы не могут быть решены с по- мощью алгоритмов из некоторого, точно определенного класса алгоритмов. Значение результата Геделя при этом зависит от степени совпадения этого алгоритмического класса и класса всех алгоритмов в интуитивном смысле. Тем самым возникла со- вершенно новая ситуация. До тех пор, пока мы верили в возможность того, что все поставленные математические задачи могут быть алгоритмически решены, у нас не было повода уточнять понятие алгоритма, вводить его математическое определение и рассматривать строгие свойства алгоритмов. Когда для решения какого-то класса проблем предлагался алгоритм, возникало соглашение считать указанный алгоритм действительно алгоритмом. Только утверждение об алгоритмической неразрешимо- сти требует строго определения, т.к. для такого доказательства требуется утвержде- ние обо всех мыслимых алгоритмах.
С появлением ЭВМ проблема теоретического анализа алгоритмов стала еще акту- альнее. Программа для ЭВМ представляет собой запись алгоритма решения задачи на каком–либо языке программирования. Для программиста программа — это после-
довательность действий, которые нужно выполнить, чтобы из исходных данных по- лучить результат. Однако такое определение алгоритма не является математически строгим и, следовательно, не позволяет рассмотреть свойства алгоритмов как свой- ства некоторых формальных объектов. Практическая реализация алгоритмов в виде программы привела к необходимости сравнения качества алгоритмов. Стало важным не просто показать разрешимость или неразрешимость какой-либо проблемы, но и оценить возможности компьютера для практического решения поставленных задач. Таким образом, необходимость рассмотрения математического определения алго-
ритма определяется несколькими причинами.
Во–первых, только при наличии формального определения алгоритма можно ставить задачу о разрешимости или неразрешимости каких–либо проблем. Если мы хотим доказать, что та или иная функция не является эффективно вычислимой, то мы прежде всего должны сформулировать точное математическое понятие эффек- тивной вычислимости. Главным результатом теории алгоритмов, как будет показано в дальнейшем, является доказательство существовании некоторых неразрешимых проблем.
Во–вторых, необходимо иметь математически точный инструмент для срав- нения различных алгоритмов решения одних и тех же задач, а также для срав- нения различных проблем по сложности алгоритмов их решения. Такое сравнение
невозможно без введения средств исследования алгоритмов как математических объ- ектов и использования точного языка математики для их описания. Иначе говоря, сами алгоритмы должны стать такими же предметами точного исследования, как те объекты, для работы с которыми они предназначены.
Прежде, чем ввести математически строгое определение алгоритма, необходимо рассмотреть свойства тех объектов, которые мы считаем алгоритмами. С точки зре- ния современной практики алгоритм — это программа, а критерием алгоритмично- сти процесса является возможность его запрограммировать. Именно благодаря этой реальности алгоритма, а также потому, что подход программиста к математическим методам всегда основан на возможности их практической реализации, можно выде- лить следующие характерные свойства, которым удовлетворяет любой алгоритм.
1. "Конечность."
Любой алгоритм задается последовательностью инструкций конечных размеров. Например, конечную длину имеет любая программа для ЭВМ, любой математиче- ский алгоритм можно описать с помощью конечного числа русских слов.
2. "Детерминированность."
Алгоритм выполняется детерминированно, т.е. представляющая алгоритм после- довательность действий на одних и тех же данных всегда выполняется одинаково. Вычисления выполняются детерминированно без обращения к случайным устрой- ствам (например, игральным костям ). Здесь следует отметить, что все программно реализованные датчики случайных чисел генерируют на самом деле псевдослучай- ную последовательность с достаточно большим периодом.
3. "Дискретность."
Отдельные инструкции алгоритма выполняются дискретно, т.е. последовательно по отдельным шагам, без использования каких–либо аналоговых устройств непре- рывного принципа действия или соответствующих непрерывных методов.
4. "Вычислимость" или "эффективная вычислимость."
Должен существовать вычислитель, способный выполнить указанные в алгорит- ме инструкции. Здесь под вычислителем может пониматься любое существующее или реализуемое устройство, способное понимать инструкции алгоритма. Частным случаем такого устройства может являться компьютер или человек. Понятие "эф-
фективная вычислимость" означает практическую выполнимость алгоритма: "эф- фективный" означает "практически выполнимый". Этот термин часто сокращают до термина "вычислимость предполагая "по умолчанию" наличие определения "эффек- тивная". В частности, свойство конечности алгоритма непосредственным образом связано с требованием вычислимости. Никакой вычислитель (человек — исполнитель алгоритма, компьютер или какое–либо другое устройство ) не может использовать более чем конечное количество информации.
5. "Конечная память."
Вычислитель должен иметь средства для хранения и отображения информации. Память вычислителя может быть сколь угодно большой, но при каждом выполнении алгоритма требуется конечный объем памяти.
6. "Результативность."
Алгоритм должен быть результативным, т.е. завершающимся с некоторым ре- зультатом после некоторого конечного числа шагов.
Таким образом, говоря неформально, алгоритм – это эффективная детерминиро- ванная конечная процедура, которую можно применять к любому элементу некото- рого класса входов и которая для каждого такого входа дает в конце концов соот- ветствующий результат. Анализ свойств алгоритмов показывает, что следует разли- чать описание алгоритма и процесс выполнения алгоритма. Несмотря на неточную формулировку, практически все программисты согласились бы с тем, что опреде- ление понятия алгоритма включает первые пять пунктов. Эти первые пять свойств должны выполняться для любого алгоритма и характеризуют его описание. В от- личие от этих свойств последнее свойство — свойство результативности — характе- ризует не описание алгоритма, а процесс его выполнения. Легко можно написать работоспособную программу, содержащую бесконечный цикл. Таким образом, опи- сание алгоритма всегда конечно, но процесс выполнения может быть бесконечным, поэтому свойство результативности алгоритма является только желательным, но не обязательным свойством алгоритмов. Более того, как будет показано в дальней- шем, общего метода проверки результативности алгоритма, применимого к любому алгоритму A и любым исходным данным x, вообще не существует.
Можно выделить три основных типа универсальных алгоритмических моделей, различающихся исходными эвристическими соображениями относительно того, что такое алгоритм. В зависимости от того, что берется за основу формализации, рас- смотрим следующие подходы к определению понятия алгоритма.
1) Частично–рекурсивные функции. Модель основана на функциональном подходе и рассматривает понятие алгоритма с точки зрения того, что можно вычислить с помощью алгоритма. Эта наиболее развитая и изученная модель является исторически первой формализацией понятия алгоритма и связывает определение алгоритма с наиболее традиционными понятиями математики — вычислениями и числовыми функциями.
2) Машины Тьюринга. Эта автоматная модель имеет в своей основе анализ процес-
са выполнения алгоритма и рассматривает алгоритм в виде набора инструкций для некоторой формальной модели вычислителя. Данный тип основан на представлении об алгоритме как о некотором детерминированном устройстве, способном выполнять в каждый отдельный момент лишь весьма примитивные операции. Такое представле- ние не оставляет сомнений в однозначности алгоритма и элементарности его шагов. Кроме того, теоретическая основа этих моделей очень близка к ЭВМ.
3) Алгоритмы Маркова. Представляет собой языковый подход к понятию алго-
ритма, в основе которого лежит формализация процесса преобразования записей исходных данных в запись результатов. Всякие исходные данные для некоторой
частной проблемы из какого–нибудь общего класса проблем могут быть сформу- лированы в виде некоторого выражения подходящего языка. Всякое решение этой проблемы в свою очередь также является выражением того или иного языка. То- гда алгоритм можно понимать как способ преобразования записи исходных данных в запись результатов. Преимущества такого типа формализации алгоритма — в его максимальной абстрактности и возможности применить понятие алгоритма к объ- ектам произвольной природы, а не обязательно числовой, как это требуется для функциональной модели. Впрочем, как мы увидим в дальнейшем, модели второго и третьего типа довольно близки на формальном уровне и различаются в основном только эвристическими признаками. На протяжении всей книги мы будем иметь дело с неотрицательными целыми числами, множествами неотрицательных целых чисел и отображениями неотрицательных целых чисел в неотрицательные целые числа. Если только не оговорено противное, мы используем термин "натуральное число" или просто "число" для обозначения неотрицательного целого числа.
Будем рассматривать формальное определение алгоритмов, выполняющих дей- ствия на множестве целых неотрицательных чисел — на самом простом множестве, на котором можно исследовать поведение алгоритмов. Как мы увидим, это ограни- чение числовыми функциями не приводит к потере общности.
Такой подход не снижает общности понятия алгоритма при условии, что любой алгоритм обрабатывает исходные данные конечной длины, причем эти данные пред- ставлены в конечном алфавите. Ограничение числовыми функциями также не при- водит к потере общности, т.к. при условии конечности алфавита и длины исходной информации эту информацию всегда можно представить некоторым натуральным числом — ее номером. Например, любая программа для ЭВМ получает на вход после- довательность байтов, которую можно считать одним очень длинным натуральным числом.
Теория алгоритмов строится на основе финитного метода. Опыт парадоксов тео-
рии множеств научил математику крайне осторожно обращаться с бесконечностью и по возможности даже о бесконечности рассуждать с помощью конечных методов. Существо финитного подхода заключается в том, что он допускает только конечные действия над конечными объектами. Выяснение того, какие объекты и действия над ними следует считать точно определенными, какими свойствами и возможностями обладают комбинации элементарных действий — все это является предметом теории алгоритмов и формальных систем.
Оператор минимизации
Вернемся к начальной цели, которую мы поставили — дать формальное опре- деление алгоритма как функции, принадлежащей некоторому конструктивно опре- деленному классу функций. Возможно, что определение примитивно–рекурсивных функций будет удовлетворять этой цели. Однако сначала надо практически убедить- ся в том, что частный случай алгоритмов — программы для ЭВМ — можно предста- вить примитивно–рекурсивными функциями. Заданные в определении примитивно– рекурсивных функций средства их конструирования позволяют использовать для на- писания алгоритмов простейшие функции, оператор суперпозиции и оператор прими- тивной рекурсии. Если рассматривать программную реализацию этих конструктив- ных элементов, то простейшие функции соответствуют некоторому базовому набору операций языка программирования, оператор суперпозиции — последовательному выполнению действий, а оператор примитивной рекурсии — рекурсивной процедуре или оператору цикла типа "for". Рассмотрим достаточность этих средств для кон- струирования любого алгоритма. Сначала введем в рассмотрение новый оператор, представляющий аналог оператора цикла типа "while". Поскольку такой цикл вы- полняется многократно при истинности некоторого условия, необходимо рассматри- вать предикаты, определяющие такие условия. Любой предикат принимает значения "ложь" и "истина с которыми нельзя производить арифметических действий. Для
того, чтобы представить значение предиката натуральным числом, введем понятие характеристической функции предиката
{ 1, P (x1, . . . , xn) = истина
χp(x1, . . . , xn) =
0, P (x1, . . . , xn) = ложь
Кстати, при реализации логических переменных в программах для ЭВМ также обычно используются именно числа 0 и 1 для машинного представления значений "ложь" и "истина".
Теперь можно дать определение специального оператора, выполняющего цикл вычислений по некоторому условию.
Определение 2.3.Функция f (x1, . . . , xn) получается оператором минимизации из предиката P (x1, . . . , xn, z), если в любой точке (x1, x2, ..., xn) значением функции f (x1, . . . , xn) является минимальное значение z, обращающее предикат P (x1, . . . , xn, z)
в истину. Оператор минимизации имеет обозначение
f (x1, . . . , xn) = µz (P (x1, . . . , xn, z)). (2.3)
Для того, чтобы для любого предиката P (x1, . . . , xn, z) найти минимальное зна- чение z, обращающее P (x1, . . . , xn, z) в истину, нужно последовательно перебирать значения z = 0, 1, 2, .... Вычисление значения функции, заданной с помощью опера- тора минимизации, можно программно реализовать следующим образом:
int f(int x1,..., int xn)
{
int z=0;
while (P(x1,... xn,z)==0) z++; return z;
}
Пример.Пусть f (x, y) = µz(2∗x+z = y+1). Предикат P (x, y, z) = (2∗x+z = y+1) является примитивно–рекурсивным, т.к. его характеристическая функция является суперпозицией примитивно–рекурсивных функций и равна
sg(sg((2x + z)−˙(y + 1)) + sg((y + 1)−˙(2x + z))).
Вычислим значение f (1, 5):
| z = 0, | P (1, 5, 0) = | Ложь, |
| z = 1, . . . z = 4, | P (1, 5, 1) = P (1, 5, 4) = | Ложь, Истина. |
Тогда f (1, 5) = 4. Рассмотрим вычисление f (5, 1). В этой точке функция не опре- делена, т.к. P (5, 1, z) = "Ложь"для любого значения z ∈ N .
Полученный пример показывает, что с помощью оператора минимизации из при- митивно–рекурсивных функций можно получить не всюду определенные функции, поэтому оператор минимизации выводит из класса примитивно–рекурсивных функ- ций. Попробуем сделать так, чтобы остаться внутри класса примитивно–рекурсивных функций, но оставить возможность использования циклов типа "while". Для этого достаточно при определении оператора минимизации ввести ограничение на измене- ние переменной z так, чтобы цикл всегда завершался после некоторого числа шагов. В общем случае такое ограничение должно являться функцией свободных перемен- ных x1, x2,...,xn.
Упражнения к разделу
Задачей выполнения упражнений является приобретение навыков даказательства примитивной или частичной рекурсивности заданной функции, усвоение принципов построения рекурсивного определения простых функций.
Задача 1
Доказать примитивную рекурсивность функции
f (x, y) = [log2(xy+2·x+ 2)].
Решение.Рассмотрим следующие вспомогательные функции:
g1(x, y) = x + y,
g2(x, y) = x · y, l
g3(x, y) = xy,
g4(x) = [log2(x + 1)].
Примитивную рекурсивность функции g1(x, y) = x + y мы доказали в 1.2. Докажем примитивную рекурсивность остальных функций. Рассмотрим сначала g2(x, y) = x · y. В соответствии с определением, некоторая функция является примитивно- рекурсивной, если выполняется одно из следующих условий:
а) эта функция является простейшей;
б) эта функция получена с помощью оператора примитивной рекурсии из функ- ций, примивная рекурсивность которых уже доказана;
в) эта функция получена с помощью оператора суперпозиции из функций, при- мивная рекурсивность которых уже доказана.
Попробуем построить схему примитивной рекурсии для функции g2(x, y). В соот-
ветствии с определением этой функции:
g2(x, 0) = x · 0 = 0 = 01(x);
g2(x, y + 1) = x · (y + 1) = x · y + x = g2(x, y) + x = g1(g2(x, y), x).
Покажем соответствие полученного рекурсивного определения функции g2(x, y) = x · y определению оператора примитивной рекурсии R и докажем примитивную ре- курсивность тех функций, из которых с помощью оператора R получена искомая функция. В соответсвии с определением, функция двух аргументов t(x, y) построена с помощью оператора R2(r, h), если она имеет вид:
t(x, 0) = r(x);
t(x, y + 1) = h(x, y, t(x, y)). (2.10)
Рассмотрим вид функций r(x) и h(x, y, z) в нашем случае:
g2(x, 0) = 01(x);
g2(x, y + 1) = g1(g2(x, y), x) = g1(I3(x, y, g2(x, y)), I3(x, y, g2(x, y)).
3 1
Таким образом, имеем
r(x) = 01(x),
h(x, y, z) = g1(I3(x, y, g2(x, y)), I3(x, y, g2(x, y)).
3 1
Суперпозиция примитивно–рекурсивных функций g1(x, y), I3(x, y, z), I3(x, y, z) при-
3 1
митивно рекурсивна, следовательно и функция g2(x, y) является примитивно–рекур-
сивной.
| In |
аргументы в том порядке, который соответствует схеме примитивной рекурсии. По- этому в дальнейшем не будем представлять функцию в форме, строго согласованной с порядком аргументов функции h(x,y,z) в (2.10). Например, для функции g3(x, y) имеем
g3(x, 0) = x0 = 1 = s(0(x));
g3(x, y + 1) = x(y + 1) = xy · y = g2(y, g3(x, y)).
Функция g3(x, y) получена оператором примитивной рекурсии из примитивно-рекур- сивных функций s(0(x)), g2(x, y) и, следовательно, примитивно-рекурсивна.
Доказательство для функции g4(x) = [log2(x+1)] выполняется с помощью ограни-
z+1
ченного оператора минимизации. Действительно, g4(x) = [log2(x+1)] = µz≤x+1(2 >
x+1), причем ограничивающая функция x+1 = s(x) и характеристическая функция
предиката
{ 0, 2z+1 ≤ x + 1
{0, 2z+1−˙(x + 1) = 0
z+1 ˙
χ(x, z) =
1, 2z+1 > x =
1, 2z+1−˙(x + 1) > 0 =sg(2
−(x + 1))
примитивно–рекурсивны. Следовательно, и g4(x) — примитивно–рекурсивная функ- ция.
Вернемся теперь к поставленной задаче доказательства примитивной рекурсив- ности функции
f (x, y) = [log2(xy+2·x + 2)] = g4(xy+2·x + 2 − 1) =
= g4(xy+2·x + 1) = g4(s(xy+2·x)) =
= g4(s(g2(x, y + 2 · x))) = g4(s(g2(x, g1(y, 2 · x)))) =
= g4(s(g2(x, g1(y, g1(x, x))))).
Функция f (x, y) является примитивно-рекурсивной как суперпозиция примитивно- рекурсивных функций.
Варианты заданий
1. f (x, y) = [log2((x + 1) · (yy+2x) + 2x] + 2 + [√y] .
2. f (x, y) = [x√3]+ [1+x+√yxy + 2x]+ 22x+y2.
...2y+2
3. f (x, y) = xyy+1 .
...2y+3
4. f (x, y) = x(y+1)(y+2) .
5. f (x) = [(x2+ x)√4 + x3+ 2x]+ [√5x3+ 2x + 1]+ 82x+2.
2x+3
6. f (x) =
∑ [√xi + 3i + ix + √2x + 2 + i] .
i=1
| y+2 |
8. f (x, y, z) = {x 3 } + [ 1+x+y xy + 2zy2] + 22x+z .
√ √ 2
9. f (x, y) = [x√4 + x2]+ [√5xy+ 2x + 1]+ 82x+y3.
10. f (x, y, z) = [(z2+ y)√4 + x3+ 2x = z4]+ [√3xz+ 2x + 1].
11. f (x, y) = [log5(yy+2·x) + x!] + [√x] + [√y] .
xx+4
i 3
| { }. |
∑ x+2 +i
4x+1+i
i=0
2x+3
13. f (x, y) =
∏ [√xi + 2i + 2y + √3y + i] .
i=1
14. f (x, y, z) =
x+z
∏
iy
| √ √ |
i=0 j=0
15. f (x) = [(x2+ y)√4 + x3+ 2x]+ [√5x3+ 2x + 1]+ 82x+2.
16. f (x) = [5x√2]+ [x+√2x + 2x4]+ 22x+2.
| y3+3 |
18. f (x, y) = [xy√x2+ y2]+ [1+√xxy + 2x]+ x2+y.
19. f (x) =
2x+3
∑
i=0
[xi+3i+ix ] 2x+2+i
| . |
| y2+2x |
Задача 2
Доказать примитивную рекурсивность функции p(x) – простое число с номером
x. В соответствии с доказательством написать программу вычисления этой функции.
Решение.Рассмотрим сначала вспомогательную функцию h(x), равную числу делителей числа x. Очевидная формула
x
h(x) = ∑(sg({x/i})),
i=1
(где выражение {x/i} означает остаток от деления x на i ) доказывает примитивную рекурсивность функции h(x), являющейся суперпозицией примитивно-рекурсивных функций. Простые числа и только они имеют ровно два делителя — единицу и самого себя. Числа 0 и 1 простыми не являются. Все числа, не являющиеся простыми, кроме 0 и 1, имеют число делителей, большее двух. Тогда характеристическая функция χp(x) предиката ⟨x — простое число при x > 1⟩ равна
χp(x) = sg(h(x)−˙2)
и является примитивно–рекурсивной.
Одной из наиболее известных арифметических функций является функция π(x), равная числу простых чисел, не превосходящих x. Используя уже известную нам примитивно–рекурсивную функцию χp(x), получим
x
π(x) = ∑(χp(i).
i=1
Отсюда следует, что искомая функция p(x) – простое число с номером x – представ- ляет собой минимальное решение уравнения
π(z) = x.
Таким образом,
p(x) = µz(π(z) = x).
Для доказательства примитивной рекурсивности функции p(x) достаточно ввести верхнюю границу изменения z и доказать примитивную рекурсивность как этой гра- ницы, так и характеристической функции предиката p(x) = x. Последнее легко сде- лать, т.к. эта функция равна
sg((π(z)−˙x) + (x−˙π(z))).
Осталось рассмотреть границу изменения z. Из теории чисел хорошо известно, что
n
pn< 22 . В самом деле, требующееся нам неравенство заведомо истинно при n = 0.
По индукции далее предполагаем, что это неравенство истинно для всех значений n, докажем его для n + 1.
Тогда
p0 < 22 ,
. . .
| n |
0 1 n
0 1 n
n+1
p0 · p1 · ... · pn + 1 < 22
· 22
· ... · 22
+ 1 = 22 +2 +...+2
+ 1 < 22 .
Число a = p0 · p1 · ... · pn+ 1 больше единицы и поэтому должно иметь какой-то про- стой делитель pr. Этот делитель не может совпадать ни с одним из простых чисел p0, p1, ...pn, так как при делении числа a на любое из чисел p0, p1, ...pnполучается остаток 1. Но все простые числа, не превосходящие pn, содержатся в последователь- ности p0 , p1 , ... pn. Число pr в нее не входит и, следовательно, pn+1 ≤ pr. Так как pr ≤ a, то
что и требовалось доказать.
pn+1 ≤ a < 22
n+1
,
Итак, неравенство доказано, а вместе с ним доказана и примитивная рекурсив- ность функции p(x), имеющей своим значением простое число с номером x.
Напишем теперь программу вычисления этой функции, соответствующую постро- енному доказательству. Сразу отметим, что доказательство примитивной рекурсив- ности функции не ставит своей целью построение алгоритма, обладающего хорошими временными характеристиками. Такое доказательство обосновывает лишь существо- вание алгоритма решения поставленной задачи, причем свойство определенности всюду для примитивно–рекурсивных функций означает, что для любых исходных данных соответствующая программа получит результат через некоторое конечное (может быть, очень большое ) время.
Приведенному выше доказательству соответствует следующая программа.
#include <stdio.h>
#include <STDLIB.H>
int sg(int x) { return x>0; }
int h(long int x)
{
long int i; int s=0;
for (i=1; i<=x; i++ ) 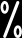 i); return s;
i); return s;
}
int Xi(long int x)
{
if (x==1) return 1; if (x==0) return 0; return 1-sg(h(x)-2);
}
long int Pi( long int x)
{
long int i,s=0;
for (i=1; i<=x; i++ )s+=Xi(i); return s;
}
long int p( long int x)
{
long int z=0;
while (Pi(z)!=x) z++; return z;
}
void main(void)
{
int x; 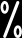 d",&x); unsigned long int z=p(x);
d",&x); unsigned long int z=p(x);
printf("простое число с номером 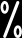 dравно
dравно 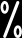 ld\n",x,z);
ld\n",x,z);
}
Следует отметить, что мы доказали алгоритм для любого x ∈ N . Однако, огра- ничение разрядной сетки компьютера не позволяет на уровне команд выполнить операции над сколь угодно большими числами. В нашей программе мы ограничили получаемые значения типом long int. Если программа должна работать с большими числами, необходимо реализовать так называемую длинную арифметику.
Варианты заданий
1. f (x) – количество ненулевых цифр в десятичной записи числа x.
2. f (x) – числитель следующего непрерывного многочлена x − − ой степени
1 + 1 .
1 + 1
1 + 1
1 + ... 1
1 +
x
Если в результате вычислений получается сократимая дробь, деление числителя и знаменателя на их наибольший общий делитель не выполнять.
3. f (x, y) – наименьшее общее кратное чисел x и y.
4. f (x, y) – минимальное простое число, принадлежащее отрезку [x, y].
5. f (x) – простое число с номером x; простые числа нумеровать, начиная от 0.
6. f (x) – количество ненулевых цифр в троичном представлении числа x.
7. f (x, y) – максимальное простое число, принадлежащее отрезку [x, y]. Если такие числа отсутствуют, значение функции равно 0.
8. f (x) – номер наибольшего простого делителя числа x, где f (0) = 0.
9. f (x) – количество единиц в шестнадцатиричном представлении числа x.
10. f (x, y) – число простых чисел, не превосходящих x + y.
11. f (x) – количество ненулевых цифр в шестнадцатиричном представлении за- данного числа x.
12. f (x) – произведение удвоенных делителей числа x.
13. f (x, y) – число простых чисел, не превосходящих x + y .
14. f (x) – нечетное число Фибоначчи с номером x. Числа Фибоначчи определя- ются следующим соотношением
F (0) = 0, F (1) = 1,
F (n) = F (n − 1) + F (n − 2) для n > 1.
Например, последовательность первых чисел Фибоначчи имеет вид:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, ...
15. f (x) – четное число Фибоначчи с номером n (см. пояснение к предшествую- щему упражнению ).
16.
| k |
четырехэлементного множества на две части:
{1, 2, 3} ∪ {4}, {1, 2, 4} ∪ {3}, {1, 3, 4} ∪ {2}, {2, 3, 4} ∪ {1},
{1, 2} ∪ {3, 4}, {1, 3} ∪ {2, 4}, {1, 4} ∪ {2.3}.
| k |
| k |
0 0
17.
| k |
| k |
| k |
произносится как "k циклов из n". Цикл [A, B, C, ..., D] равен циклу [B, C, ..., D, A], поскольку конец цикла соединен с его началом. Таким образом, для цикла из четырех элементов выполняется равенство
[A, B, C, D] = [B, C, D, A] = [C, D, A, B] = [D, A, B, C] .
Существует одиннадцать различных способов составить два цикла из четырех эле- ментов:
[1, 2, 3] [4] , [1, 2, 4] [3] , [1, 3, 4] [2] , [2, 3, 4] [1] ,
[1, 3, 2] [4] , [1, 4, 2] [3] , [1, 4, 3] [2] , [2, 4, 3] [1] ,
[1, 2] [3, 4] , [1, 3] [2, 4] , [1, 4] [2.3] .
18.
| k |
вок множества {1, 2, 3..., n}, имеющих k участков подъема, т.е. k мест в перестановке
ства {1, 2, 3, 4} (из всех 4! = 34 перестановок ) содержат по два участка подъема:
1324, 1423, 2314, 2413, 3412,
1243, 1342, 2341;
2134, 3124, 4123.
В первой строке перечислены перестановки с отношениями a1 < a2 > a3 < a4, во второй строке перечислены перестановки с отношениями a1 < a2 < a3 > a4, и в третьей – с отношениями a1 > a2 < a3 < a4.
19. f (x) – числитель несократимого гармонического числа с номером x. Гармони- ческим числом называется
1 1 1 n 1
∑
Hn = 1 + 2 + 3 + ... + n =
k
k=1
20. f (x) – знаменатель несократимого гармонического числа с номером x (см. пред- шествующее задание ).
Глава 1
ЧАСТИЧНО – РЕКУРСИВНЫЕ ФУНКЦИИ
Свойства алгоритмов
Под алгоритмом решения задач некоторого класса обычно понимается общее правило, с помощью которого решение любой конкретной проблемы этого класса может быть найдено чисто механически и без всяких дополнительных размышлений о процессе решения. Среди известных примеров – алгоритм Евклида нахождения наибольшего общего делителя для двух натуральных чисел, алгоритм деления двух целых чисел, алгоритм перевода целого десятичного числа в двоичную систему счис- ления и т.п. Для любой задачи алгоритм ее решения должен быть доказан. Даже если на некотором наборе тестов соответствующая программа для ЭВМ выдала правиль- ный результат, принципиальное отсутствие доказательства правильности алгоритма может означать только одно: предлагаемый алгоритм решает какую–то другую за- дачу, возможно, являющуюся частным случаем поставленной задачи.
Слово "алгоритм" происходит от имени арабского математика Мохаммеда ибн Муса Альхваризми, который в IX столетии внес значительный вклад в разработку и практическое применение методов вычислений. Прогресс в развитии таких методов породил представление о том, что можно найти алгоритм решения любой поставлен- ной математической и даже философской проблемы. Вера в универсальность алго- ритмических методов была впервые подорвана работой Геделя, в которой была дока- зана алгоритмическая неразрешимость некоторых математических проблем. Точнее, было доказано, что известные математические проблемы не могут быть решены с по- мощью алгоритмов из некоторого, точно определенного класса алгоритмов. Значение результата Геделя при этом зависит от степени совпадения этого алгоритмического класса и класса всех алгоритмов в интуитивном смысле. Тем самым возникла со- вершенно новая ситуация. До тех пор, пока мы верили в возможность того, что все поставленные математические задачи могут быть алгоритмически решены, у нас не было повода уточнять понятие алгоритма, вводить его математическое определение и рассматривать строгие свойства алгоритмов. Когда для решения какого-то класса проблем предлагался алгоритм, возникало соглашение считать указанный алгоритм действительно алгоритмом. Только утверждение об алгоритмической неразрешимо- сти требует строго определения, т.к. для такого доказательства требуется утвержде- ние обо всех мыслимых алгоритмах.
С появлением ЭВМ проблема теоретического анализа алгоритмов стала еще акту- а
