Xiii. The pythagorean property
The ancient Egyptians discovered that in stretching ropes of lengths 3 units, 4 units and 5 units as shown below, the angle formed by the shorter ropes is a right angle. 2. The Greeks succeeded in finding other sets of three numbers which gave right triangles and were able to tell without drawing the triangles which ones should be right triangles, their method being as follows. 3. If you look at the illustration you will see a triangle with a dashed interior. 4. Each side of it is used as the side of a square. 5. Count the number of small triangular regions in the interior of each square. 6. How does the number of small triangular regions in the two smaller squares compare with the number of triangular regions in the largest square? 7. The Greek philosopher and mathematician Pythagoras noticed the relationship and is credited with the proof of this property known as the Pythagorean Theorem or the Pythagorean Property. 8. Each side of a right triangle being used as a side of a square, the sum of the areas of the two smaller squares is the same as the area of the largest square.
 |
Proof of the Pythagorean Theorem
9. We should like to show that the Pythagorean Property is true for all right triangles, there being several proofs of this property. 10. Let us discuss one of them. 11. Before giving the proof let us state the Pythagorean Property in mathematical language. 12. In the triangle above, c represents the measure of the hypotenuse, and a and b represent the measures of the other two sides.

 | ||||||||
 | ||||||||
 | ||||||||
 | ||||||||
 | ||||||||
13. If we construct squares on the three sides of the triangle, the area-measure will be a2, b2 and c2. 14. Then the Pythagorean Property could be stated as follows: c2 = a2 + b2. 15. This proof will involve working with areas. 16. To prove that c2 = a2 + b2 for the triangle above, construct two squares each side of which has a measure a + b asshown above. 17. Separate the first of the two squares into two squares and two rectangles as shown. 18. Its total area is the sum of the areas of the two squares and the two rectangles.
A = a2+2ab+b2
19. In the second of the two squares construct four right triangles. 20. Are they congruent? 21. Each of the four triangles being congruent to the original triangle, the hypotenuse has a measure c. 22. It can be shown that PQRS is a square, and its area is c2. 23. The total area of the second square is the sum of the areas of the four triangles and the square PQRS. A = c2+4 (½ ab). The two squares being congruent to begin with2, their area measures are the same. 25. Hence we may conclude the following:
a2+2ab+b2 = с2+4(½ ab)
(a2 + b2) + 2ab = c2 + 2ab
26. By subtracting 2ab from both area measures we obtain a2+ b2 = c2 which proves the Pythagorean Property for all right triangles.
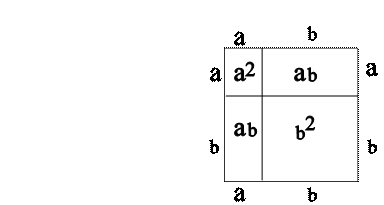
XIV. SQUARE ROOT
1. It is not particularly useful to know the areas of the squares on the sides of a right triangle, but the Pythagorean Property is very useful if we can use it to find the length of a side of a triangle. 2. When the Pythagorean Property is expressed in the form c2 = a2 + b2, we can replace any two of the letters with the measures of two sides of a right triangle. 3. The resulting equation can then be solved to find the measure of the third side of the triangle. 4. For example, suppose the measures of the shorter sides of a right triangle are 3 units and 4 units and we wish to find the measure of the longer side. 5. The Pythagorean Property could be used as shown below:
c2 = a2+b2, c2 = 32+42, c2 = 9+16, c2 = 25.
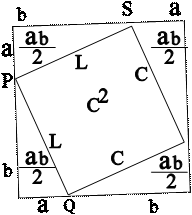
6. You will know the number represented by c if you can find anumber which, when used as a factor twice, gives a product of 25. 7. Of course, 5x5 = 25, so c = 5 and 5 is called the positive square root (корень) of 25. 8. If a number is a product of two equal factors, then either (любой) of the equal factors is called a square root of the number. 9. When we say that y is the square root of K we merely (вcero лишь) mean that y2 = K. 10. For example, 2 is a square root of 4 because 22 = 4. 11. The product of two negative numbers being a positive number, —2 is_also a square root of 4 because (—2)2 = 4. The following symbol √ called a radical sign is used to denote thepositive square root of a number. 13. That is √K means the positive square root of K. 14. Therefore √4 =2 and √25 = 5. 15. But suppose you wish to find the √20. 16. There is no integer whose square is 20, which is obvious from the following computation. 42= 16 so √16 = 4; a2 = 20 so 4<a<5, 52 = 25, so √25 = 5. 17. √20 is greater than 4 but less than 5. 18. You might try to get a closer approximation of √20 by squaring some numbers between 4 and 5. 19. Since √20 is about as near to 42 as¹ to 52, suppose we square 4.4 and 4.5.
4.42= 19.36 a2 = 20 4.52 = 20.25
20. Since 19.36<20<20.25 we know that 4.4<a<4:5. 21. 20 being nearer to 20.25 than to 19.36, we might guess that √20 is nearer to 4.5 than to 4.4. 22. Of course, in order to make sure2 that √20 = 4.5, to the nearest tenth, you might select values between 4.4 and 4.5, square them, and check the results. 23. You could continue the process indefinitely and never get the exact value of 20. 24. As a matter of fact, √20 represents an irrational number which can only be expressed approximately as rational number. 25. Therefore we say that √20 = 4.5 approximately (to the nearest tenth).
APPENDIX
SAMPLE TEST FROM GMAT
1. A trip takes 6 hours to complete. After traveling ¼ of an hour, 1⅜ hours, and 2⅓ hours, how much time does one need to complete the trip?
(A) 2 ¹/¹² hours
(B) 2 hours, 2½ minutes
(C) 2 hours, 5 minutes
(D) 2⅛ hours
(E) 2 hours, 7½ minutes
2. It takes 30 days to fill laboratory dish with bacteria. If the size of the bacteria doubles each day, how long did it take for the bacteria to fill one half of the dish?
(A) 10 days
(B) 15 days
(C) 24 days
(D) 29 days
(E) 29.5 days
3. A car wash can wash 8 cars in 18 minutes. At this rate how many cars can the car wash wash in 3 hours?
(A) 13
(B) 40.5
(C) 80
(D) 125
(E) 405
4. If the ratio of the areas of 2 squares is 2 : 1, then the ratio of the perimeters of the squares is
(A) 1: 2
(B) 1: √2
(C) √2 : 1
(D) 2 : 1
(E) 4: 1
5. There are three types of tickets available for a concert: orchestra, which cost $12 each; balcony, which cost $9 each; and box, which cost $25 each. There were P orchestra tickets, B balcony tickets, and R box tickets sold for the concert. Which of the following expressions gives the percentage of the ticket proceeds due to the sale of orchestra tickets?
P
(A)100 x ¾¾¾¾¾
(P+B+R)
P
(B) 100 x ¾¾¾¾¾¾¾¾¾
(12P + 9B + 25 R)
P
(C) ¾¾¾¾¾¾¾¾¾
(12P + 9B + 25 R)
(9B + 25R)
(D) 100 x ¾¾¾¾¾¾¾¾¾
(12P + 9B + 25 R)
(12P + 9B +25R)
(E) 100 x ¾¾¾¾¾¾¾¾¾
(12P)
6. City B is 5 miles east of City A. City C is 10 miles southeast of City B. Which of the following is the closest to the distance from City A to City C?
(A) 11 miles
(B) 12 miles
(C) 13 miles
(D) 14 miles
(E) 15 miles
7. If 3x – 2y = 8, then 4y – 6x is:
(A) -16
(B) -8
(C) 8
(D) 16
(E) cannot be determined
8. It costs 10c. a kilometer to fly and 12c. a kilometer to drive. If you travel 200 kilometers, flying x kilometers of the distance and driving the rest, then the cost of the trip in dollars is:
(A) 20
(B) 24
(C) 24 – 2x
(D) 24 – 0.02x
(E) 2.400 – 2x
9. If the area of a square increases by 69%, then the side of the square increases by:
(A) 13%
(B) 30%
(C) 39%
(D) 69%
(E) 130%
10. There are 30 socks in a drawer. 60% of the socks are red and rest are blue. What is the minimum number of socks that must be taken from the drawer without looking in order to be certain that at least two blue socks have been chosen?
(A) 2
(B) 3
(C) 14
(D) 16
(E) 20
11. How many squares with sides ½ inch long are needed to cover a rectangle that is 4 feet long and 6 feet wide?
(A) 24
(B) 96
(C) 3,456
(D) 13,824
(E) 14,266
12. In a group of people solicited by a charity, 30% contributed $40 each, 45 % contributed $20 each, and the rest contributed $12 each. What percentage of the total contributed came from people who gave $40?
(A) 25%
(B) 30%
(C) 40%
(D) 45%
(E) 50%
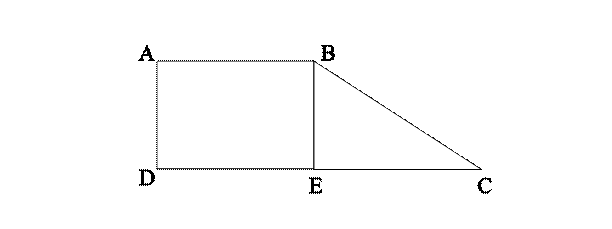
13. A trapezoid ABCD is formed by adding the isosceles right triangle BCE with base 5 inches to the rectangle ABED where DE is t inches. What is the area of the trapezoid in square inches?
(A) 5t + 12.5
(B) 5t + 25
(C) 2.5t + 12.5
(D) (t + 5)²
(E) t² + 25
14. A manufacturer of jam wants to make a profit of $75 by selling 300 jars of jam. It costs 65c. each to make the first 100 jars of jam and 55c. each to make each jar after the first 100. What price should be charged for the 300 jars of jam?
(A) $75
(B) $175
(C) $225
(D) $240
(E) $250
15. A car traveled 75% of the way from town A to town B by traveling for T hours at an average speed of V mph. The car travels at an average speed of S mph for the remaining part of the trip. Which of the following expressions represents the time the car traveled at S mph?
(A) VT/ S
(B) VS/4T
(C) 4VT/3S
(D) 3S/VT
(E) VT/3S
16. A company makes a profit of 7% selling goods which cost $2,000; it also makes a profit of 6% selling a machine that cost the company $5,000. How much total profit did the company make on both transactions?
(A) $300
(B) $400
(C) $420
(D) $440
(E) $490
17. The ratio of chickens to pigs to horses on a farm can be expressed as the triple ratio 20: 4: 6. If there are 120 chickens on the farm, then the number of horses on the farm is
(A) 4
(B) 6
(C) 24
(D) 36
(E) 60
18. If x² - y² = 15 and x + y =3, then x – y is
(A) – 3
(B) 0
(C) 3
(D) 5
(E) cannot be determined
19. What is the area of the shaded region? The radius of the outer is a and the radius of each of the circles inside the large circle is a/3.
(A) 0
(B) (⅓)pa²
(C) (⅔)pa²
(D) (⁷/₉)pa²
(E) (⁸/₉)pa²

20. If 2x – y = 4, then 6x – 3y is
(A) 4
(B) 6
(C) 8
(D) 10
(E) 12
21. A warehouse has 20 packers. Each packer can load ⅛of a box in 9 minutes. How many boxes can be loaded in 1½hours by all 20 packers?
(A) 1¼
(B) 10¼
(C) 12½
(D) 20
(E) 25
22. In Motor City 90% of the population own a car, 15 % own a motorcycle, and everybody owns one or the other or both. What is the percentage of motorcycle owners who own cars?
(A) 5 %
(B) 15 %
(C) 33⅓ %
(D) 50 %
(E) 90 %
23. Towns A and C are connected by a straight highway which is 60 miles long.
The straight-line distance between town A and town B is 50 miles, and the straight-line distance from town B to town C is 50 miles. How many miles is it from town B to the point on the highway connecting towns A and C which is closest to town B?
(A) 30
(B) 40
(C) 30√2
(D) 50
(E) 60
24. A chair originally cost $ 50.00. The chair was offered for sale at 108% of its cost. After a week the price was discounted 10% and the chair was sold. The chair was sold for
(A) $45.00
(B) $48.60
(C) $49.00
(D) $49.50
(E) $54.00
25. A worker is paid x dollars for the first 8 hours he works each day. He is paid y dollars per hour for each hour he works in excess of 8 hours. During one week he works 8 hours on Monday, 11 hours on Tuesday, 9 hours on Wednesday, 10 hours on Thursday, and 9 hours on Friday. What is his average daily wage in dollars for the five-day week?
(A) x + (7/5) y
(B) 2x + y
(C) (5x + 8y)/ 5
(D) 8x + (7/5) y
(E) 5x+7y
26. A club has 8 male and 8 female members. The club is choosing a committee of 6 members. The committee must have 3 male and 3 female members. How many different committees can be chosen?
(A) 112,896
(B) 3,136
(C) 720
(D) 112
(E) 9
27. A motorcycle costs $ 2,500 when it is brand new. At the end of each year it is worth ⁴/₅ of what it was at the beginning of the year. What is the motorcycle worth when it is three years old?
(A) $1,000
(B) $1,200
(C) $1,280
(D) $1,340
(E) $1,430
28. If x + 2y = 2x + y, then x – y is equal to
(A) 0
(B) 2
(C) 4
(D) 5
(E) cannot be determined
29. Mary, John, and Karen ate lunch together. Karen’s meal cost 50% more than John’s meal and Mary’s meal cost ⁵/₆ as much as Karen’s meal. If Mary paid $2 more than John, how much was the total that the three of them paid?
(A) $2833
(B) $30.00
(C) $35.00
(A) $37.50
(B) $40.00
30. If the angles of triangle are in the ratio 1 : 2 :2, then the triangle
(A) is isosceles
(B) is obtuse
(C) is a right triangle
(D) is equilateral
(E) has one angle greater than 80º
31. Successive discounts of 20% and 15% are equal to a single discount of
(A) 30%
(B) 32%
(C) 34%
(D) 35%
(E) 36%
32. It takes Eric 20 minutes to inspect a car. Jane only needs 18 minutes to inspect a car. If they both start inspecting cars at 8:00 a.m., what is the first time they will finish inspecting a car at the same time?
(A) 9:30 a.m.
(B) 9:42 a.m.
(C) 10:00 a.m.
(D) 11:00 a.m.
(E) 2:00 p.m.
33. If x/y = 4 and y is not 0, what percentage (to the nearest percent) of x is
2x – y
(A) 25
(B) 57
(C) 75
(D) 175
(E) 200
34. If x > 2 and y > - 1, then
(A) xy > - 2
(B) – x < 2y
(C) xy < - 2
(D) –x > 2y
(E) x < 2y
35. If x = y =2z and x●y● z = 256, then x equals
(A) 2
(B) 2 ³√2
(C) 4
(D) 4 ³√2
(E) 8
36. If the side of square increases by 40%, then the area of the square increases by
(A) 16%
(B) 40%
(C) 96%
(D) 116%
(E) 140%
37. If 28 cans of soda cost $21.00, then 7 cans of soda should cost
(A) $5.25
(B) $5.50
(C) $6.40
(D) $7.00
(E) $10.50
38. If the product of 3 consecutive integers is 210, then the sum of the two smaller integers is
(A) 5
(B) 11
(C) 12
(D) 13
(E) 18
39. Both circles have radius 4 and the area enclosed by both circles is 28º. What is the area of the shaded region?
 |
(A) 0
(B) 2p
(C) 4p
(D) 4p²
(E) 16p
40. If a job takes 12 workers 4 hours to complete, how long should it take 15 workers to complete the job?
(A) 2 hr 40 min
(B) 3 hr
(C) 3 hr 12 min
(D) 3 hr 24 min
(E) 3 hr 30 min
41. If a rectangle has length L and the width is one half of the length, then the area of the rectangle is
(A) L
(B) L²
(C) ½ L²
(D) ¼ L²
(E) 2L
42. What is the next number in the arithmetic progression 2, 5, 8 .......?
(A) 7
(B) 9
(C) 10
(D) 11
(E) 12
43. The sum of the three digits a, b, and c is 12. What is the largest three-digit number that can be formed using each of the digits exactly once?
(A) 921
(B) 930
(C) 999
(D) 1,092
(E) 1,200
44. What is the farthest distance between two points on a cylinder of height 8 and the radius 8?
(A) 8 √2
(B) 8 √3
(C) 16
(D) 8 √5
(E) 8 (2p + 1)
45. For which values of x is x² - 5x + 6 negative?
(A) x < 0
(B) 0 < x < 2
(C) 2 < x < 3
(D) 3 < x < 6
(E) x > 6
46. A plane flying north at 500 mph passes over a city at 12 noon. A plane flying east at the same time altitude passes over the same city at 12:30p.m. The plane is flying east at 400 mph. To the nearest hundred miles, how far apart are the two planes at 2 p.m.?
(A) 600 miles
(B) 1,000 miles
(C) 1,100 miles
(D) 1,200 miles
(E) 1,300 miles
47. A manufacturer of boxes wants to make a profit of x dollars. When she sells 5,000 boxes it costs 5¢ a box to make the first 1,000 boxes and then it costs y¢ a box to make the remaining 4,000 boxes. What price in dollars should she charge for the 5,000 boxes?
(A) 5,000 + 1,000y
(B) 5,000 + 1,000y + 100x
(C) 50 + 10y + x
(D) 5,000 + 4,000y + x
(E) 50 +40y + x
48. An angle of x degrees has the property that its complement is equal to ¹/₆ of its supplement where x is
(A) 30
(B) 45
(C) 60
(D) 63
(E) 72
49. The angles of a triangle are in the ratio 2 : 3 : 4. The largest angle in the triangle is
(A) 30º
(B) 40º
(C) 70º
(D) 75º
(E) 80º
50. If x < y, y < z, and z > w, which of the following statements is always true?
(A) x > w
(B) x < z
(C) y = w
(D) y > w
(E) x < w
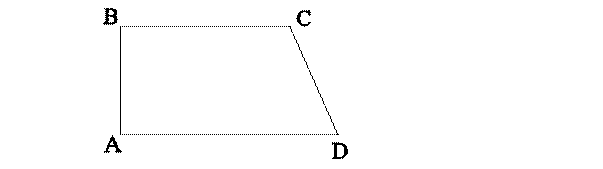
51 ABCD has area equal to 28. BC is parallel to AD. BA is perpendicular to AD. If BC is 6 and AD is 8, then what is CD?
(A) 2√2
(B) 2√3
(C) 4
(D) 2√5
(E) 6
52. Write formulas according to descriptions:
1. a plus b over a minus b is equal to c plus d over c minus d.
2. a cubed is equal to the logarithm of d to the base c.
3. a) j of z is equal to b, square brackets, parenthesis, z divided by с sub m plus 2. close parenthesis, to the power m over m minus 1, minus 1, close square brackets;
b) j of z is equal to b multiplied by the whole quantity: the quantity two plus z over с sub m, to the power m over m minus 1, minus1.
4. the absolute value of the quantity j sub j of t one, minus j sub j of t two, is less than or equal to the absolute value of the quantity M of t₁ minus b over j, minus M of t₂ minus b over j.
5. R is equal to the maximum over j of the sum from i equals one to i equals n of the modulus of aij of t, where t lies in the closed interval a b and where j runs from one to n.
6. the limit as n becomes infinite of the integral of f of s and j n of s plus delta n of s, with respect to s, from t to t, is equal to the integral of f of s and j of s, with respect to s, from t to t.
7. y sub n minus r sub s plus 1 of t is equal to p sub n minus r sub s plus 1, times e to the power t times l sub q plus s.
8. L sub n adjoint of g is equal to minus 1 to the n, times the n-th derivative of a sub zero conjugate times g, plus, minus one to the n minus 1, times the n minus first derivative of a sub one conjugate times g, plus ... plus a sub n conjugate times g.
9. the partial derivative of F of lambda sub i of t and t, with respect to lambda, multiplied by lambda sub i prime of t, plus the partial derivative of F with arguments lambda sub i of t and t, with respect to t, is equal to 0.
10. the second derivative of y with respect to s. plus y, times the quantity 1 plus b of s, is equal to zero.
11. f of z is equal to j sub mk hat, plus big 0 of one over the absolute value of z, as absolute z becomes infinite, with the argument of z equal to gamma.
12. D sub n minus 1 prime of x is equal to the product from s equal to zero to n of, paranthesis, 1 minus x sub s squared, close paranthesis, to the power epsilon minus 1.
13. K of t and x is equal to one over twopi, times the integral of K of t and z, over w minus w of x, with respect to w along curve of the modulus of w minus one half, is equal to rho.
14. The second partial (derivative) of u with respect to t, plus a to the fourth power, times the Laplacian of the Laplacian of u, is equal to zero, where a is positive.
15. D sub k of x is equal to one over two pi, times integral from c minus i infinity to c plus i infinity of dzeta to the k of, w, x to the w divided by w, with respect to w, where c is greater than 1.
ACTIVE VOCABULARY
Предлагаемый словарь содержит выражения, которые были представлены в данном пособии как новая лексика. Слова и выражения расположены в алфавитном порядке.
-А-
| абсолютная величина, абсолютное значение | absolute value |
| абсолютный, полный квадрат | perfect square |
| абсцисса | abscissa |
| алгебра | algebra |
| аксиома | axiom |
| аксиома завершенности | completeness axiom |
| аксиома поля | field axiom |
| аксиома порядка | order axiom |
| алгебраическая кривая | algebraic curve |
| анализ | analysis |
| антилогарифм | antilogarithm |
| аргумент, независимая переменная | argument |
| арифметика | arithmetic |
| арка, дуга | arc |
| апофема | apothem |
| ассоциативный | associative |
-Б-
| безопасный | secure |
| бесконечный(о) | infinite(ly) |
| бесконечно малое приращение | increment |
| бесконечный предел | infinite limit |
| бесконечная производная | infinite derivative |
| бесконечный ряд | infinite series |
| боковой, латеральный | lateral |
-В-
| вводить | to introduce |
| величина, значение | value |
| вертикальный | vertical |
| вершина (вершины) | vertex (vertices) |
| ветвь (у гиперболы) | branch |
| внешний (угол) | exterior |
| вносить вклад | to contribute |
| внутренние точки | interior points |
| внутренний (угол) | interior |
| вогнутый | concave |
| воображаемый | fictitious |
| вписанный круг | inscribed circle |
| вращение | rotation |
| выбирать | to select |
| выбор | choice |
| выводить, получать, извлекать (о знании) | to derive |
| выдающийся | distinguished |
| выпуклый | convex |
| вырожденный | degenerating |
| вырождаться | to degenerate |
| высота под наклоном | slant height |
| высота треугольника | altitude |
| вычисление | computation |
| вычислять | compute |
-Г-
| геометрическое место точек | locus (pl. loci) |
| горизонтальный | horizontal |
| гнуть, сгибать, изгибать | to bend (bent-bent) |
| грань | face |
| грань, фаска, ребро | edge |
| градиент | gradient |
| график | graph |
-Д-
| двучленный, биноминальный | binomial |
| действовать | to operate |
| действительное число | геаl number |
| делать вывод | to conclude |
| делимое | dividend |
| делитель | divisor |
| десятичный логарифм | соmmоn logarithm |
| детерминант, определитель | determinant |
| директриса | directrix (pl. Dirextrices) |
| дискриминант | discriminant |
| дистрибутивный | distributive |
| дифференциальное исчисление | differential calculus |
| дифференцирование | differentiation |
| додекаэдр, двенадцатигранник | dodecahedron |
| дробь | fraction |
| доказывать | to prove |
| доказательство | proof |
| дуга, арка | arc |
-Е-
| Евклидова геометрия | Euclidean geometry |
-И-
| идентичный | identical |
| изгиб, наклон | slope |
| измерение, мера, предел, степень | measure |
| изнурение, истощение, исчерпание | exhaustion |
| изображение, образ, отражение | image |
| изобретать | to invent |
| икосаэдр, двадцатигранник | icosahedron |
| икосидодекаэдр, тридцатидвухгранник | icosidodecahedron |
| интеграл | integral |
| интегральное исчисление | integral calculation |
| интегрирование | integration |
| интервал | interval |
| интерпретация | interpetation |
| иррациональный | irrational |
| иррациональность | irrationality |
| исчисление | calculus |
-З-
| замкнутый, закрытый | closed |
| закрытая кривая | closed curve |
| закрытый интервал | close interval |
| зеркальное отражение | mirror image |
| знаменатель | denominator |
| значительный | significant |
-К-
| касательная | tangent |
| касательная плоскость | tangent plane |
| касаться | to concern |
| кратное число | multiple |
| квадрант, четверть круга | quadrant |
| квадратный (об уравнениях) | quadratic |
| коммутативный | commutative |
| комплексное | complex |
| комплексное число | complex nuber |
| комплектовать | to complete |
| конгруэнтный | congruent |
| конечный | finite |
| конический | conic |
| конфигурация, очертание | configuration |
| копланарный, расположеннный в одной плоскости | coplanar |
| кривая | curve |
| кривизна | curvature |
| круглый, круговой | circular |
| кубическое | cubic |
| кубооктаэдр, трехгранник | cuboctahedron |
-Л-
| линейный | linear |
| линия отсчета | reference line |
| логарифм | logarithm |
-М-
| мантисса | mantissa |
| математический | mathematical |
| мгновенный, моментальный | instantaneous |
| метод бесконечно малых величин | infinitesimal method |
| многогранник | polyhedron |
| многогранный, полиэдрический | polyhedral |
| многочленный | polynomial |
| многоугольник | polygon |
| множество | set |
| множитель, фактор | factor |
| момент инерции | moment оf inertia |
-Н-
| наклонная линия, косая линия | oblique |
| направление | direction |
| направленные числа | directed numbers |
| натуральный логарифм | natural logarithm |
| начало координат | origin |
| начальная ось | initial axis |
| независимый | independent |
| неизменный | unvarying |
| непрерывная, функция | continuous function |
| неопределенный | undefined |
| неуловимый | elusive |
| нулевой угол | null angle |
-О-
| обобщать | to generalize |
| обозначать | to denote |
| обозревать | to review |
| общее значение | total |
| общий | in commоn |
| образующая поверхности | generator - generatrix |
| обратная величина | reciprocal |
| обратно | conversely |
| объем | volume |
| одновременный | simultaneous |
| однозначное соответствие, отображение | one-to-one mapping |
| однообразный | uniform |
| октаэдр, восьмигранник | octahedron |
| определять | to determine |
| ордината | ordinate |
| основной, главный | principal |
| ось | axis |
| открытый | open |
| открытая кривая | open curve |
| отношение | relation |
| отражать | to ret1ect |
| отрезок | segment |
| отрицательный | negative |
| очевидный | obvious |
-П-
| параллелограмм | parallelogram |
| пентаграмма | pentagram |
| переменная величина, функция | fluent |
| пересекаться | to intersect |
| перпендикулярный | perpendicular |
| пирамида | pyramid |
| Платонов, относящийся к Платону | Platonic |
| плоскостная кривая | plane curve |
| плоскостной, плоский | planar |
| плоскость, плоскостной | plane |
| площадь всей поверхности | total surface area |
| поверхность | surface |
| подмножество | subset |
| подразделяться, распадаться на | to fall (fell,fallen) into |
| подразумевать | to imply |
| подчиняться правилам (законам) | to оbеу laws |
| познакомиться с | to bе familiar (with) |
| полный угол | round angle |
| положительный | positive |
| полуправильный | semiregular |
| понятие | notion |
| понятие, концепт | concept |
| по часовой стрелке | clockwise |
| против часовой стрелки | anticlockwise |
| правильный (о многоугольниках и т.д.) | regular |
| предел отношения | limit оf а ratio |
| предельный случай | limiting case |
| предполагать | to assume, to suppose |
| представлять | to imagine, tо represent |
| преобразование | translation |
| призма | prism |
| применение | application |
| приписывать | to credit |
| проекция | projection |
| произведение | product |
| производная | derivative |
| производная, флюксия | fluxion |
| простой | simple |
| простое (число) | prime |
| противоречить | to contradict |
| противоречие | contradiction |
| процедура | procedure |
| прямой | straight |
| пятиугольник | pentagon |
| пятиугольный | pentagonal |
-Р-
| равносторонний | equilateral |
| равноугольный | equiangular |
| радиус | radius |
| развернутый угол | flat angle |
| развитие | development |
| разлагать | to resolve |
| разложение множителей | factorization |
| располагаться между | to lie between |
| рассматривать | to regard |
| расстояние | distance |
| рациональный | rational |
| решать | to solve |
| рост | growth |
-С-
| сводить в таблицу | tabulаtе |
| свойство | property |
| сечение | section |
| система прямоугольных координат | Cartesian coordinates |
| система записи | notation |
| скорость, быстрота | velociy |
| скорость изменения | rate of change |
| сложение | addition |
| сокращать | to canсеl |
| сокращать, преобразовывать | to reduce |
| соответствовать | tо correspond |
| средний | mean |
| средняя величина (значение) | average |
| ссылаться на | to refer (to) |
| степень | degree |
| стереографический | stereographic |
| сторона (в уравнении) | side |
| сфера | sphere |
| сумма | sum |
| существовать | to exist |
-Т-
| таблица | tablе |
| твердое тело | solid |
| тетраэдр, четырехгранник | tetrahedron |
| точка | point |
| трансцендентный | transcendental |
| треугольный, трехсторонний | triangular |
| трехмерный, объемный, пространственный | three-dimensional |
-У-
| увеличивать | to enlarge |
| угол понижения (падения) | depression angle |
| угол возвышения | elevation angle |
| удлиненный | elongated |
| удобство | convenience |
| удовлетворять | to satisfy |
| указывать | to indicate |
| умножение | multiplication |
| уравнение | equation |
| усекать, обрезать; отсекать верхушку | to truncate |
| ускорение | acceleration |
| установить | to estabIish |
-Х-
| характеристика | charaсteristic |
-Ц-
| целый, весь, полный | entire |
| целое число | integer |
| цель | purpose |
| центр массы (тяжести) | centroid |
-Ч-
| частное | quotient |
| часть | unit |
| числа со знаками | signed numbers |
| числитель | numerator |
| числа со знаками | signed numbers |
-Ш-
| шестиугольник | hexagon |
| шестиугольный | hexagonal |
-Э-
| элемент, составная часть | element |
| элементарный | elementary |
| эллипс | ellipse |
| эллиптический | elliptical |
