Представить графически фактические, расчетные и прогнозные значения

Для построения графика (рис. 15) воспользуемся сводной таблицей 6.

Таблица 6

X	Y	Yp
		31.65
		37.07
		45.2
		39.78
		56.04
		64.17
		75.01
		69.59
		85.85
		115.66
		97.69
		133.63

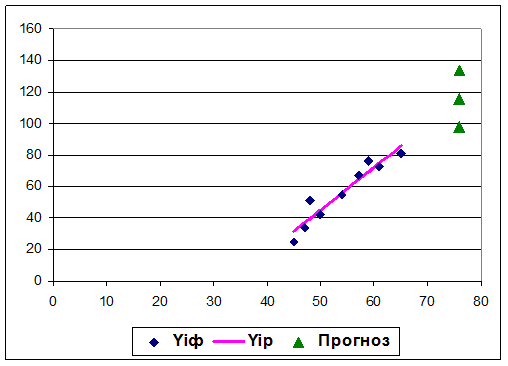
Рис. 15. График моделирования и прогнозирования по модели парной линейной регрессии

Парная нелинейная регрессия

Общий вид регрессионной модели:

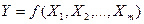. (1)

Если в уравнении (1) присутствует только один фактор X, а f – нелинейная математическая функция, получим парную нелинейную модель регрессии вида

Y=f(X).

Парная линейная регрессия проста в использовании, удобна и наглядна. Но среди реальных экономических данных линейные зависимости встречаются нечасто. Поэтому в эконометрических исследованиях чаще применяются нелинейные модели (рис. 16).

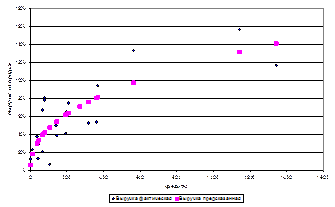
а) гиперболическая функция может использоваться для показателей, достигающих насыщения, начиная с определенных значений фактора (верхняя горизонтальная асимптота);

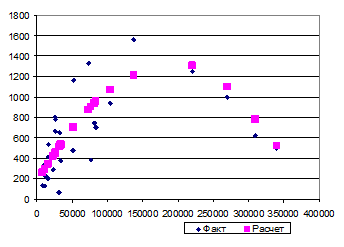
б) парабола применяется в тех случаях, когда исследуемая величина меняет направление своего развития;

в) затухающие колебания могут характеризовать объемы продаж сезонного товара на этапе ухода с рынка.

Рис. 16. Примеры нелинейных зависимостей

Различают два класса нелинейных регрессий:

1) регрессии, нелинейные относительно объясняющих переменных, но линейные по оцениваемым параметрам;

2) регрессии, нелинейные как относительно объясняющих переменных, так и относительно оцениваемых параметров.

К первому классу относятся, например:

1) полиномы разных степеней

;

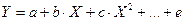2) равносторонняя гипербола

.

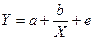Ко второму классу относятся:

1) степенная функция

;

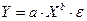2) показательная

;

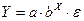3) экспоненциальная

.

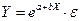Работа с такими моделями сводится к их предварительной линеаризации (приведению к линейному виду). Модели из первого класса приводятся к линейному виду простой заменой переменных. Для линеаризации моделей второго класса используют полулогарифмическую функцию или логарифмирование. Полученные таким образом вспомогательные линейные модели оценивают обычным МНК. Затем осуществляют обратный переход к нелинейной функции.

Замечание.

Если модель второго класса с помощью соответствующих преобразований может быть приведена к линейному виду, то она называется внутренне линейной, если же модель не может быть сведена к линейной функции, то она называется внутренне нелинейной (например, 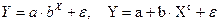и другие). Для оценки параметров таких моделей используются итеративные процедуры.

Кривые Энгеля и Филлипса[8]

Примером использования равносторонней гиперболы 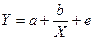являются кривые Филлипса и Энгеля.

Кривая Филлипса 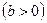показывает взаимное изменение уровней безработицы (х) и инфляции в экономике (или процента прироста заработной платы) (y). Названа по имени английского экономиста А. Филлипса, который впервые представил графики подобного рода в 1958 г. (рис. 17).

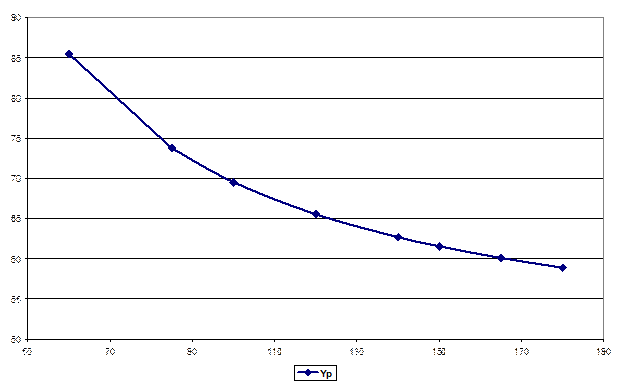
Рис. 17. Кривая Филлипса

Такая форма кривой (обратная зависимость с нижней горизонтальной асимптотой) показывает, что инфляция (или прирост заработной платы) высока при низкой безработице и низка – при высокой. Соответственно можно определить тот уровень безработицы, при котором заработная плата оказывается стабильной и темп ее прироста равен нулю.

Кривая Энгеля 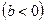показывает величину расходов на товары в зависимости от роста дохода. Эта взаимосвязь была впервые проанализирована в 19 в. немецким статистиком Э. Энгелем. Закон Энгеля устанавливает, что доля расходов на продовольственные товары по мере роста дохода падает, т.к. продукты питания относятся к необходимым товарам. В то же время с увеличением дохода доля расходов на непродовольственные товары будет возрастать. При этом можно определить границу величины дохода, дальнейшее увеличение которого не приводит к росту доли расходов на отдельные непродовольственные товары (имеем медленно повышающуюся функцию с верхней горизонтальной асимптотой, рис. 18).

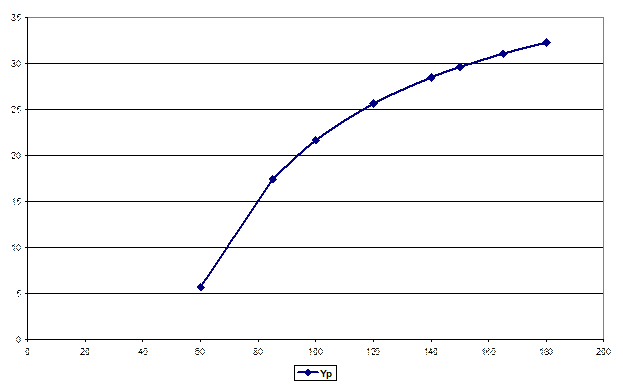
Рис. 18. Кривая Энгеля

Кривая Энгеля полезна также при определении степени влияния на спрос дохода и изменений в относительных ценах.

Пример

Пусть зависимая переменная y – средняя заработная плата продавцов (в тыс. руб.) в семи различных торговых точках, а фактор x – чистая среднемесячная прибыль (в тыс. руб.) в них (исходные данные приведены в таблице 1).

Таблица 1

n	y	x

Требуется:

1. Построить степенную, показательную и гиперболическую модели нелинейной регрессии. Результаты моделирования отобразить на графике.

2. Сравнить качественные характеристики моделей, рассчитав коэффициенты детерминации и средние относительные ошибки аппроксимации.

Решение:

Степенная модель

.

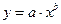Линеаризация:

,

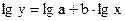обозначим lg y=Y, lg x= X, и получим вспомогательную линейную модель вида

Y=A+bX.

Для ее построения воспользуемся таблицей 2 (столбцы X=lg x и Y=lg y) и результатами регрессионного анализа.

Таблица 2

n	y	x	lg y=Y	lg x=X	yp	ei	ei^2	eiотн	y-ycp	(y-ycp)^2
			0.301	1.699	2.464	-0.464	0.215	23.200	-14.286	204.082
			0.602	1.778	4.097	-0.097	0.009	2.427	-12.286	150.939
			1.041	1.929	10.823	0.177	0.031	1.606	-5.286	27.939
			1.230	1.929	10.823	6.177	38.151	36.333	0.714	0.510
			1.255	2.000	17.030	0.970	0.941	5.389	1.714	2.939
			1.447	2.079	28.317	-0.317	0.101	1.133	11.714	137.224
			1.531	2.146	43.527	-9.527	90.773	28.022	17.714	313.796
Сумма							130.222	98.110		837.429
Среднее	16.286	91.429						14.016

Вспомогательная линейная модель примет вид

Y=-4.346+2.789*X.

Обратный переход к степенной функции:

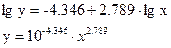
Степенная модель парной регрессии примет вид:

.

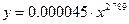С помощью этой модели рассчитываем все последующие столбцы таблицы 1, начиная с 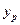и далее.

Качественные характеристики модели:

–

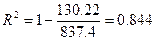84.4 % случайной вариации переменной средняя заработная плата (y) учтено в построенной модели и обусловлено случайными колебаниями фактора чистая прибыль (х);

–

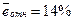фактические значения средней зарплаты отличаются от рассчитанных на основе степенной модели в среднем на 14 %.

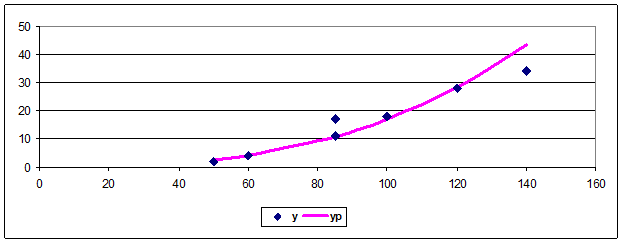
График:

x	y	yp
		2.464
		4.097
		10.823
		10.823
		17.030
		28.317
		43.527

Показательная модель

.

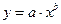Линеаризация:

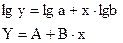
Таблица 3

n	y	x	lg y=Y	yp	ei	ei^2	eiотн
			0.301	3.119	-1.119	1.252	55.954
			0.602	4.245	-0.245	0.060	6.125
			1.041	9.173	1.827	3.339	16.611
			1.230	9.173	7.827	61.265	46.042
			1.255	14.564	3.436	11.807	19.089
			1.447	26.976	1.024	1.048	3.657
			1.531	49.967	-15.967	254.929	46.960
Сумма						333.700	194.439
Среднее	16.286	91.429					27.777

Y=-0.161+0.0133*x – вспомогательная линейная модель.

Обратный переход:

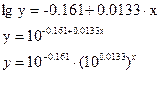
Окончательно показательная модель примет вид:

.

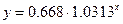Качественные характеристики модели:

–

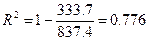77,6 % случайной вариации переменной средняя заработная плата (y) учтено в построенной модели и обусловлено случайными колебаниями фактора чистая прибыль (х);

–

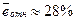фактические значения средней зарплаты отличаются от рассчитанных на основе модели в среднем на 28 %, модель неточная.

График:

x	y	yp
		3.119
		4.245
		9.173
		9.173
		14.564
		26.976
		49.967

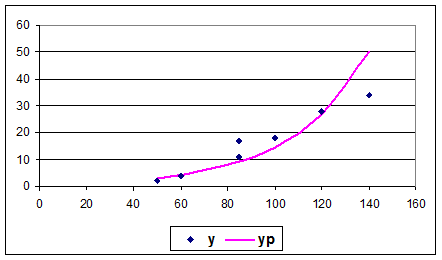
Гиперболическая модель

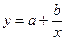
Линеаризация:

используем простую замену ,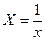

.

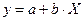Таблица 4

n	y	x	1/x=X	yp	ei	ei^2	eiотн
			0.02	-2.298	4.2983	18.475	214.9137
			0.0167	5.6834	-1.683	2.8338	42.08507
			0.0118	17.421	-6.421	41.231	58.37421
			0.0118	17.421	-0.421	0.1774	2.477429
			0.01	21.647	-3.647	13.299	20.25976
			0.0083	25.638	2.3624	5.581	8.437161
			0.0071	28.488	5.5118	30.38	16.21119
Сумма						111.98	362.7585
Среднее	16.286	91.429					51.82265

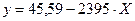– вспомогательная линейная модель;

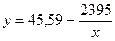– гиперболическая модель.

Качественные характеристики модели:

–

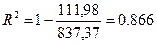86,6 % случайной вариации переменной средняя заработная плата (y) учтено в построенной модели и обусловлено случайными колебаниями фактора средняя чистая прибыль (х);

–

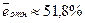фактические значения средней зарплаты отличаются от рассчитанных на основе модели в среднем на 51,8 %, модель неточная.

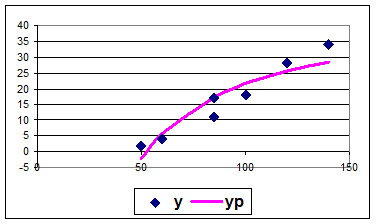
График:

x	y	yp
		-2.298
		5.6834
		17.421
		17.421
		21.647
		25.638
		28.488

Сравнение моделей

Таблица 5

Модель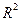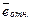
Степенная	0.844	14.02
Показательная	0.776	27.78
Гипербoлическая	0.866	51.8