Проверка статистической значимости уравнения регрессии и его параметров

а) проверка статистической значимости уравнения:

Проверка значимости (существенности) уравнения регрессии позволяет установить, существенна ли связь включенных в уравнение признаков (Y и X), соответствует ли математическая модель, выражающая зависимость Y и X, фактическим данным и достаточно ли включенных в уравнение объясняющих переменных Х для описания зависимой переменной Y. Иными словами оценка значимости уравнения регрессии позволяет узнать пригодно ли оно для практического использования (например, для прогнозирования) или нет.

Оценка значимости уравнения регрессии проводится с помощью F-критерия Фишера:

или в терминах коэффициента детерминации

,

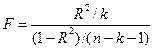где n – длина совокупностей данных, k – количество факторов, включенных в модель (в уравнении парной регрессии k=1).

Уравнение регрессии статистически значимо, если

.

Замечания:

1) 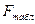определяется максимальной величиной отношения дисперсий , которая может иметь место при случайном их расхождении для данного уровня вероятности наличия нулевой гипотезы (нулевая гипотеза о незначимости уравнения в целом);

2) для определения 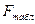можно использовать статистическую функцию FРАСПОБР, предварительно задав три параметра , где 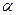– заданный уровень значимости проверки или уровень вероятности ( 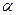связано с вероятностью Р формулой 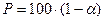); 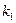– число степеней свободы числителя, равное количеству k факторов, включенных в модель; – число степеней свободы знаменателя (n-k-1). Таким образом, 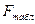зависит от заданной вероятности, числа уровней в совокупностях данных и вида уравнения регрессии.

Пример (продолжение).

4) Проверить значимость уравнения регрессии с помощью F-критерия Фишера ( 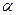=0,05)

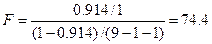
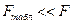
вывод: уравнение регрессии статистически значимо, связь включенных в него признаков существенна;

Значение F-критерия можно получить также в таблице «Дисперсионный анализ» отчета по работе с инструментом регрессия (рис. 13).

Дисперсионный анализ
	df	SS	MS	F
Регрессия		2834.50	2834.50	74.2
Остаток		267.50	38.21
Итого		3102.00

Рис. 13. Фрагмент регрессионного анализа

■

а) проверка статистической значимости параметров уравнения:

В линейной регрессии обычно оценивается значимость не только уравнения регрессии, но и отдельных его параметров. Для этого применяется t-критерий Стьюдента:

1) рассчитывают стандартные ошибки (среднеквадратические отклонения) 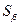и 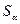каждого из параметров уравнения 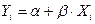по формулам

, ,

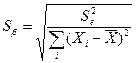где 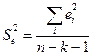–остаточная дисперсия, k – число факторов в уравнении регрессии (в нашем случае k=1);

2) определяют расчетные значения t-критерия Стьюдента:

, ;

3) определяют табличное значение t-критерия с помощью статистической функции СТЬЮДРАСПОБР по двум параметрам: заданному уровню значимости 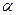и одной степени свободы (n-k-1);

4) параметры уравнения регрессии будут статистически значимы, если выполняются неравенства:

, .

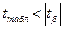Замечания:

1) статистическая значимость (незначимость) коэффициента регрессии 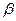означает одновременно статистическую значимость (незначимость) фактора Х, включенного в уравнение; статистически незначимый (или несущественный) фактор должен быть устранен из модели или заменен другим;

2) статистическая значимость (незначимость) параметра уравнения 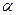означает верную (неверную) спецификацию модели; под спецификацией понимают:

а) выбор вида уравнения;

б) определение независимых факторов для включения в модель;

3) t-критерий можно использовать также для определения интервальных оценок параметров модели:

,

.

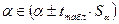Поскольку коэффициент регрессии 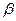в эконометрических исследованиях имеет четкую экономическую интерпретацию, доверительные границы интервала для коэффициента регрессии не должны содержать противоречивых результатов, то есть не должны содержать одновременно положительные и отрицательные величины и даже нуль.

Пример (продолжение).

4) осуществить проверку значимости параметров уравнения регрессии по t-критерию Стьюдента ( 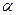=0,05)

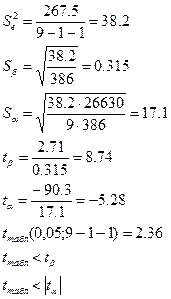
Вывод: оба параметра модели статистически значимы.

Дополнение: интервальные оценки параметров

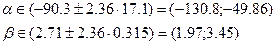
Расчетные значения t-критерия, а также интервальные оценки параметров можно найти в отчете по результатам работы с инструментом Регрессия (рис. 14).

	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%
Y	-90.33	17.12	-5.28	0.00	-130.80	-49.86
X	2.71	0.31	8.61	0.00	1.97	3.45

Рис. 14. Фрагмент регрессионного анализа

■

2.4. Экономический прогноз

Рассматриваемая модель 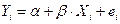может быть использована для определения прогнозных оценок исследуемой величины. При прогнозировании на основе регрессионных моделей можно выделить три основных этапа:

1) точечный прогноз фактора Х;

2) точечный прогноз показателя Y;

3) интервальный прогноз показателя Y.

Рассмотрим содержание этих этапов подробнее.

1) точечный прогноз фактора Хв зависимости от специфики исходных данных и условия задачи можно определить одним из следующих способов:

а) если исходные данные являются временными рядами, то для прогноза фактора можно воспользоваться методами экстраполяции и использовать наиболее подходящую модель временного ряда

.

Тогда прогноз фактора на k шагов вперед определяется по формуле

.

б)вслучае временных рядов можно найти также с помощью среднего абсолютного прироста (САП) по формуле

, .

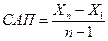в)если исходные данные являются пространственными, то, очевидно, в задаче будет задано правило для определения . Например, если прогнозное значение фактора составляет 80 % от его среднего значения, то .

2) точечный прогноз показателя Yнаходят подстановкой в модель прогнозных значений фактора:

– в случае пространственных данных,

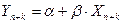– в случае временных рядов.

3) интервальный прогноз показателя Y:

вначале находят ошибку прогнозирования

,

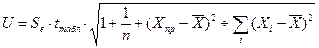которая зависит от стандартной ошибки модели 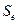, удаления от своего среднего значения, количества наблюдений n, заданного уровня вероятности попадания в интервал прогноза (он определяет величину ;

затем находят сам доверительный интервал прогноза:

нижняя граница интервала – ,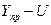

верхняя граница интервала – .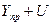

Пример (продолжение).

5) осуществить прогнозирование среднего значения показателя Y при уровне значимости 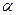=0,1, если прогнозное значение фактора Х составит 117 % от его максимального значения

1) точечный прогноз фактора Х

,

2) точечный прогноз показателя Y

3) интервальный прогноз показателя Y

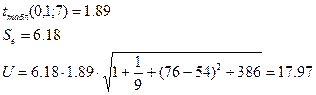
Нижняя граница интервала: 115,66-17,97=97,69

Верхняя граница интервала: 115,66+17,97=133,63.