Отбор факторов в модель множественной регрессии

Факторы, включаемые в модель множественной регрессии должны отвечать следующим требованиям:

- быть количественно измеримы

- не должны быть коррелированы между собой и те более находиться в точной функциональной связи

Отбор факторов в эконометрическую модель множественной регрессии может быть осуществлен на основе:

- сравнения остаточной дисперсии до и после включения фактора в модель

- матрицы парных коэффициентов корреляции.

- определения t-статистики для параметров регрессии.

При отборе факторов в модель множественной регрессии оценить целесообразность включения каждого из них можно используя:

- коэффициент частной корреляции.

- коэффициент множественной детерминации.

Интеркорреляция – это корреляционная связь между двумя факторами

Мультиколлинеарность –это корреляционная связь между несколькими факторами

Для оценки мультиколлинеарности факторов может использоваться определитель матрицы парных коэффициентов корреляции между факторами. Если факторы не коррелированы между собой, то матрица парных коэффициентов корреляции между факторами была бы единичной. Поскольку все недиагональные элементы были бы равны нулю.
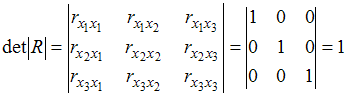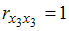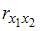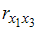, поскольку = = и = = =0.
Если между факторами существует полная линейная зависимость и все коэффициенты парной корреляции равны единице, то определитель такой матрицы равен нулю.

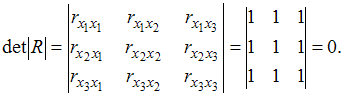
Чем ближе к нулю определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И, наоборот, чем ближе к единице определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов.

Прогнозирование по модели множественной регрессии.

Прогнозирование по модели множественной регрессии проводится аналогично прогнозированию по модели парной регрессии.

Точечный прогноз для заданных значений факторов

находится по уравнению регрессии

где В – вектор-столбец оценок параметров уравнения регрессии.

Для построения интервального прогноза для заданного уровня доверительной вероятности нужно найти стандартную (среднюю ) ошибку прогноза se(y_пр) и критическое значение t-статистики Стьюдента для 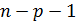степеней свободы и заданной доверительной вероятности.

Стандартная ошибка прогноза находится по формуле

где s – стандартная ошибка регрессии, для которой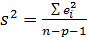

X – матрица выборки значений факторов, - матрица-столбец прогнозных значений факторов.

Доверительный интервал прогноза задается формулой

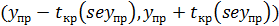
Предпосылки МНК

Условия, необходимые для получения несмещенных, состоятельных и эффективных оценок представляют собой предпосылки МНК, соблюдение которых желательно для получения достоверных результатов регрессии.

К предпосылкам МНК относятся следующие условия:

- случайный характер остатков

- нулевая средняя величина остатков, не зависящая от х_i

- гомоскедастичность (дисперсия каждого отклонения 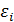одинакова для всех значений х )

- отсутствие автокорреляции остатков. Значения остатков 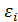распределены независимо друг от друга

- остатки подчиняются нормальному распределению

Гетероскедастичность остатков означает, что дисперсия каждого отклонения 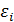неодинакова для разных значений

К тестам, позволяющим выявить наличие гетероскедастичности остатков относят тесты Гольдфельда-Квандта, ранговой корреляции Спирмэна, Уайта, Парка, Глейзера.

Шаги параметрического теста Гольдфельда-Квандта:

Шаг 1 Упорядочение n наблюдений по мере возрастания переменной х

Шаг 2 Исключение из рассмотрения С центральных наблюдений; при этом 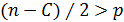, где p – число оцениваемых параметров.

Шаг 3 Разделение совокупности из (n-C) наблюдений на две группы (соответственно с малыми и большими значениями фактора х) и определение по каждой из групп уравнений регрессии.

Шаг 4 Определение остаточной суммы квадратов для первой ( 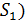и второй ( 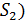групп и нахождение их отношения: 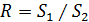, где .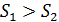

К методам определения автокорреляции остатков относятся:

- визуальный (построение графика зависимости остатков от времени)

- аналитический (использование критерия Дарбина-Уотсона)

Если в остатках существует полная положительная автокорреляция то значение критерия Дарбина-Уотсона 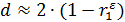равно 0

Если в остатках существует полная отрицательная автокорреляция то значение критерия Дарбина-Уотсона 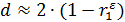равно 4

Если автокорреляция остатков отсутствует то значение критерия Дарбина-Уотсона 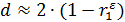равно 2

Шаги алгоритма выявления автокорреляции остатков на основе критерия Дарбина-Уотсона:

Шаг 1 Выдвигается гипотеза Н₀ об отсутствии автокорреляции остатков. Альтернативные гипотезы Н₁ и Н₁^* состоят соответственно в наличии положительной или отрицательной автокорреляции остатков.

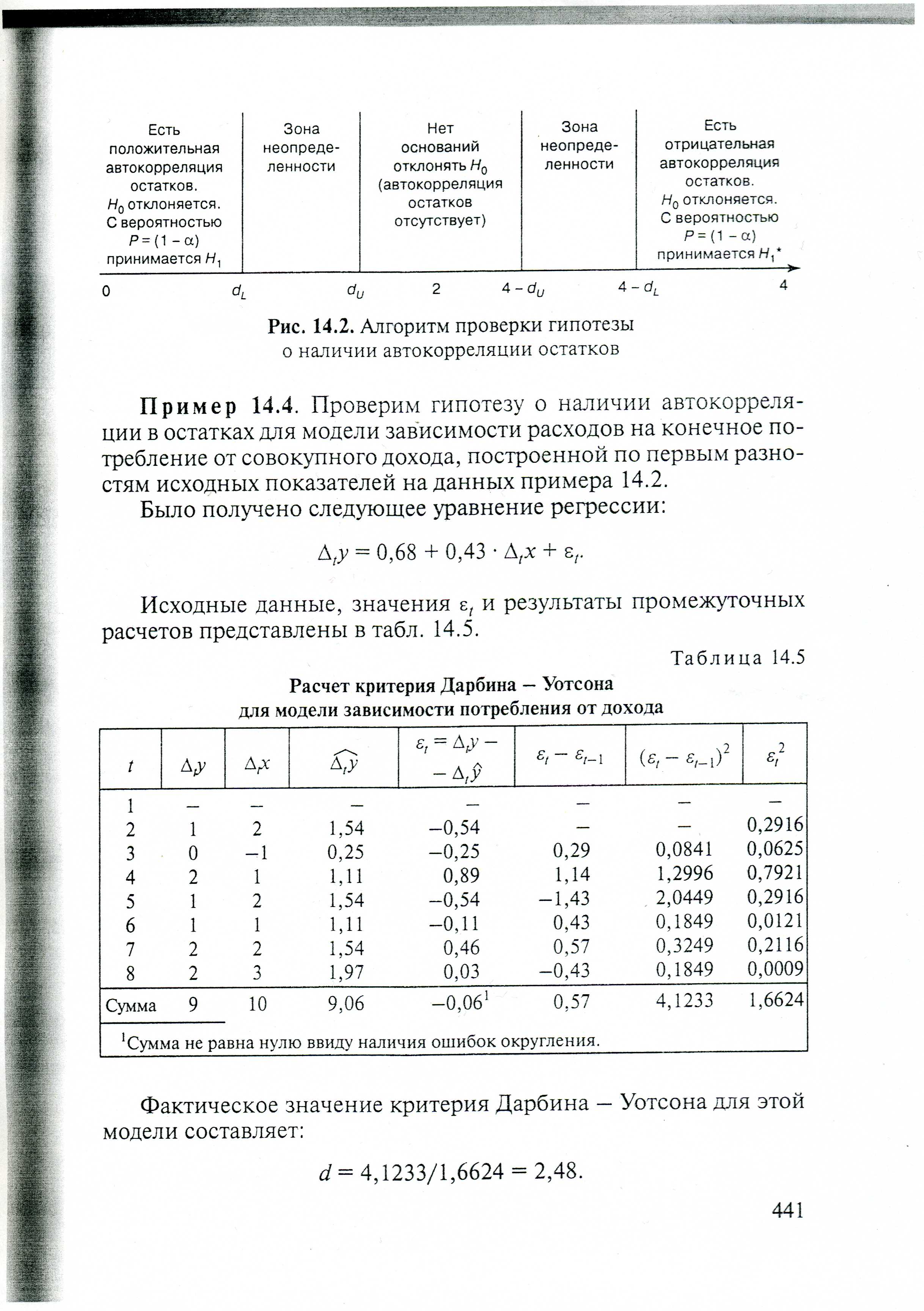
Шаг2 По специальным таблицам определяются критические значения критерия Дарбина-Уотсона d_L и d_U для заданного числа наблюдений n, числа независимых переменных модели k и уровня значимости α. По этим значениям числовой промежуток [0,4] разбивают на пять отрезков.

Шаг3 Принимают или отклоняют каждую из гипотез с вероятностью (1- α) по соответствующей шкале.

Если фактическое значение критерия Дарбина-Уотсона попадает в зону неопределенности, то предполагают существование автокорреляции остатков и отклоняют гипотезу Н₀

Если фактическое значение критерия Дарбина-Уотсона 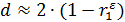попадает в интервал от 0 до d_L то можно сказать, что есть положительная автокорреляция остатков

Если фактическое значение критерия Дарбина-Уотсона 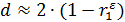попадает в интервал от (4- d_L ) до 4. В этом случае можно сказать, что есть отрицательная автокорреляция остатков

Если фактическое значение критерия Дарбина-Уотсона 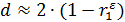попадает в интервал от d_U до (4- d_U). В этом случае можно сказать, что автокорреляция остатков отсутствует

В случае нарушений предпосылок метода наименьших квадратов применяют обобщенный метод наименьших квадратов, который используется для оценки параметров линейных регрессионных моделей с автокоррелированными и/или гетероскедастичными остатками

При использовании обобщенного метода наименьших квадратов расчеты параметров уравнения регрессии с учетом значений ковариационной матрицы остатков 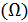могут быть проведены по формуле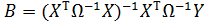

Фиктивные переменные

Фиктивная переменная может принимать значения 0 или 1.

С помощью фиктивной переменной можно в уравнении регрессии количественным образом оценить влияние качественных признаков.

При построении регрессионной модели может возникнуть ситуация, когда необходимо включить в уравнение помимо количественных переменных переменные, отражающие некоторые атрибутивные признаки (пол, образование, регион и т.п.). Такого рода качественные переменные называются «фиктивными» (dummy) переменными. Они отражают неоднородность исследуемой статистической совокупности и используются для более качественного моделирования зависимостей в таких неоднородных объектах наблюдения. При моделировании отдельных зависимостей по неоднородным данным можно также воспользоваться способом разделения всей совокупности неоднородных данных на несколько отдельных совокупностей, количество которых равно количеству состояний dummy-переменной.