Тема 4. Системы линейных одновременных уравнений
Использование одного регрессионного уравнения в экономических исследованиях часто оказывается недостаточным. На практике ряд факторных переменных чаще всего влияет на целый набор взаимозависимых результирующих переменных. Так, при оценке эффективности производства нельзя руководствоваться только моделью рентабельности. Она должна быть дополнена моделью производительности труда, а также моделью себестоимости единицы продукции. В качестве факторных переменных, при этом, могут выступать показатели квалификации сотрудников, обеспечения необходимыми средствами производства, удалённости от рынков сбыта и другие.
В том же Примере 1, помимо объёма продаж нас будут интересовать сумма затрат и прибыль. При этом сумма затрат будет зависеть от объёма продаж, а прибыль от обеих этих исследуемых переменных.
Таким образом, возникает потребность рассмотрения систем эконометрических уравнений. Выделяются три основных вида систем эконометрических уравнений: система независимых уравнений, система рекурсивных уравнений и система одновременых уравнений.
В общем случае уравнения могут быть нелинейными, однако здесь мы ограничимся рассмотрением систем линейных уравнений.
Система линейных независимых уравнений имеет следующий общий вид:
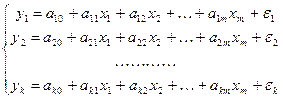(4.1)
Уравнения системы независимых уравнений могут рассматриваться самостоятельно в произвольном порядке, то есть к каждому их них применимы все операции, которые мы рассматривали выше для линейных уравнений.
Если зависимая (исследуемая переменная) одного уравнения выступает в качестве факторных переменной в последующих уравнениях, то может быть построена модель в виде системы линейных рекурсивных уравнений:
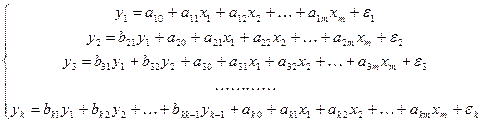. (4.2)
Уравнения системы рекурсивных уравнений также могут рассматриваться по отдельности. В случае системы линейных уравнений параметры модели могут определяться с помощью МНК. При выполнении прогнозных значений необходимо будет производить вычисления последовательно, начиная с первого уранвения.
Наибольшее распространение в эконометрических исследованиях получила система одновременных (взаимозависимых) уравнений. В ней одни и те же зависимые (исследуемые) переменные в одних уравнениях входят в левую часть, а других – в правую часть системы. Даже в простейшем случае системы одновременных линейных уравнений (eё также называют структурной формой модели – СФМ) :
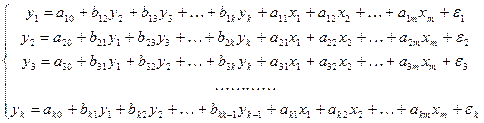. (4.3)
определение параметров модели сталкивается с большими трудностями и не всегда возможно в принципе. Для нахождения параметров модели исходная система одновременных линейных уравнений сводится к приведённой форме модели (ПФМ), которая имеет вид системы независимых переменных:
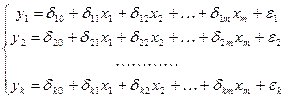(4.1)
Такое сведение всегда возможно произвести с помощью алгебраических преобразований исходной системы уравнений. Параметры приведённой системы δij можно находить с помощью МНК. Основная трудность заключается в том, что не всегда возможно по коэффициентам приведённой системы восстановить коэффициенты исходной системы уравнений, то есть осуществить обратный переход (подобно тому, как мы это делали, сводя нелинейное уравнение к линейному, находя параметры линейной модели, а затем производя обратный пересчёт параметров нелинейной модели).
Проблема перехода от приведённой формы (ПФМ) системы уравнений к исходной СФМ называется проблемой идентификации. Различаются идентифицируемые, неидентифицируемые и сверхидентифицируемые модели.
1. Модель идентифицируема, если все коэффициенты исходной модели определяются однозначно, единственным образом по коэффициентам приведённой модели. Это возможно когда число параметров исходной модели равно числу параметров приведённой формы (здесь и далее не учитывается число свободных коэффициентов в уравнениях). Процедура нахождения коэффициентов идентифицируемой модели носит название косвенного метода наименьших квадратов (КМНК) и содержит следующие этапы:
а) исходная модель преобразуется в приведённую форму модели;
б) для каждого уравнения приведённой формы модели применяется обычный МНК;
в) коэффициенты приведённой модели трансформируются в коэффициенты исходной модели.
2. Модель неидентифицируема, если число параметров приведённой системы меньше чем, число параметров исходной модели, и в результате коэффициенты исходной модели не могут быть оценены через коэффициенты приведённой формы.
3. Модель сверхидентифицируема, если число приведённых коэффициентов больше числа коэффициентов в исходной модели. В этом случае на основе коэффициентов приведённой формы можно получить два и более значений одного коэффициента исходной модели. Сверхидентифицируемая модель в отличие от неидентифицируемой модели практически разрешима, но требует специальных методов исчисления параметров. Наиболее распространённым является двух шаговый метод наименьших квадратов (ДНМК). Основная идея ДНМК – на основе приведённой формы модели получить для сверхидентифицируемого уравнения (имеются критерии для определения идентифицируемости каждого уравнения исходной системы) теоретические значения исследуемых переменных, содержащегося в правой части уравнения. Далее, подставив эти значения вместо фактических значений (результатов наблюдений), применяется МНК к сверхидентифицируемому уравнению исходной системы.
Для того, чтобы модель была идентифицируема, необходимо, чтобы каждое уравнение модели было идентифицируемо. Если хотя бы одно уравнение СФМ неидентифицируемо, то вся модель считается неидентифицируемой.
Рассмотрим необходимые и достаточные условия идентифицируемости отдельного уравнения модели.
Необходимым условием идентифицируемости отдельного уравнения модели является счетное правило. Если обозначить через Н число исследуемых переменных yl, присутствующих в i-м уравнении, а через D обозначить число факторных переменных xj, отсутствующих в i-м уравнении, то счётное правило формулируется следующим образом:
- если D + 1 < H, то уравнение неидентифицируемо;
- если D + 1 = H, то уравнение идентифицируемо;
- если D + 1 > H, то уравнение сверхидентифицируемо.
Достаточное условие идентифицируемости отдельного уравнения модели выполняется, если определитель матрицы, составленной из коэффициентов в других уравнениях при переменных (как исследуемых y, так и факторных x), отсутствующих в данном i-м уравнении не равен нулю, а ранг этой матрицы, одновременно, не меньше, чем количество всех исследуемых переменных в системе уравнениё за вычетом 1.
Пример 4.1.Дана структурная модель:
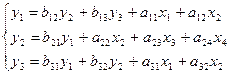
Необходимо проверить каждое уравнение системы на выполнение необходимого и достаточного условия идентифицируемости и сделать вывод об идентифицируемости системы уравнений в целом.
Всего в системе присутствуют три исследуемые переменные y1, y2, y3 и четыре факторные переменные x1, x2, x3 и x4.
В первом уравнении три исследуемые переменные: y1, y2, y3 (H=3). В нём отсутствуют две факторные переменные: x3 и x4 (D=2). Необходимое условие идентифицируемости D + 1 = H выполняется. Для проверки достаточного условия составим матрицу из коэффициентов при отсутствующих в первом уравнении x3 и x4 , взятых во втором и третьем уравнениях:
| Уравнения, из которых взяты коэффициенты при переменных | Переменные | |
| x3 | x4 | |
| a23 | a24 | |
Во второй строке матрицы стоят нули, поскольку x3 и x4 отсутствуют в третьем уравнении. Определитель такой матрицы равен нулю. Значит, достаточное условие не выполнено, и первое уравнение нельзя считать идентифицируемым. Следовательно, и вся система не является идентифицируемой. Тем не менее проверим, являются ли другие уравнения системы идентифицируемыми.
Во втором уравнении присутствуют две исследуемые переменные: y1, y2 (H=2). В нём же отсутствует одна факторная переменная x1 (D=1). Необходимое условие идентифицируемости D + 1 = H выполняется. Для проверки достаточного условия составим матрицу из коэффициентов при отсутствующих во втором уравнении y3 и x1 , взятых в первом и третьем уравнениях:
| Уравнения, из которых взяты коэффициенты при переменных | Переменные | |
| y3 | x1 | |
| b13 | a11 | |
| -1 | a31 |
 |
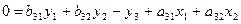В третьем уравнении (вторая строка таблицы) при y3 коэффициент равен -1, так как эта переменная стоит в левой части уравнения. Третье уравнение можно записать в виде
и тогда равенство b33 = -1 становится очевидным. Определитель матрицы не равен нулю. Ранг матрицы равен 2, что совпадает с числом исследуемых переменных минус один. Значит, достаточное условие выполняется, и второе уравнение является идентифицируемым.
В третьем уравнении присутствуют три исследуемые переменные: y1, y2, y3 (H=3). В нём отсутствует две факторные переменные x3 и x4 (D=2). Необходимое условие идентифицируемости D + 1 = H выполняется. Для проверки достаточного условия составим матрицу из коэффициентов при отсутствующих в третьем уравнении x3 и x4 , взятых во первом и втором уравнениях:
| Уравнения, из которых взяты коэффициенты при переменных | Переменные | |
| x3 | x4 | |
| a23 | a24 |
Определитель такой матрицы равен нулю. Следовательно, достаточное условие не выполняется, и третье уравнение нельзя считать идентифицируемым.
В итоге мы получили что идентифицируемым является только второе уравнение, а первое и третье уравнения не являются идентифицируемыми, поэтому система в целом не является идентифицируемой.
Рассмотрим на примере применение косвенного метода наименьших квадратов (косвенного МНК).
Пример 4.2. Пусть дана идентифицируемая модель из двух уравнений, содержащая две исследуемые и две факторные переменные:
.
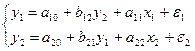Задан набор фактических данных:
| № наблюдения | y1 | y2 | x1 | x2 |
| 33,0 | 37,1 | |||
| 45,9 | 49,3 | |||
| 42,2 | 41,6 | |||
| 51,4 | 45,9 | |||
| 37,4 | ||||
| 49,3 | 52,3 |
Решение: Исходную модель можно преобразовать в приведённую форму модели вида:
.
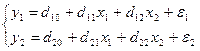Приведённая форма модели является системой независимых уравнений, к каждому из которых для нахождения коэффициентов можно применить МНК, подобно тому, как это делается для построения линейной модели множественной регрессии, состоящей из одного уравнения. Для нахождения коэффициентов первого уравнения мы применим в MS Excel обработку Cервис/ Анализ данных/ РЕГРЕССИЯ выбрав в качестве диапазона данных для исследуемой переменной колонку данных для y1, а в качестве диапазона данных для факторных переменных – колонки данных для x1 и x2. Аналогично для определения коэффициентов второго уравнения применим обработку РЕГРЕССИЯ, взяв данные для y1 , x1 и x2. В итоге получим следующую систему уравнений (ПФМ):
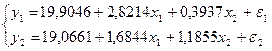
Для перехода от приведённой формы к структурной форме модели найдём x2 из второго уравнения:
.
 |
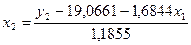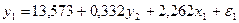Подставим это выражение в первое уравнение вместо x2 , и после необходимых арифметических преобразований, получим первое уравнение структурной формы:
Далее выразим x1 из первого уравнения ПФМ
 |
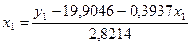
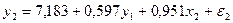и подставим это выражение во второе уравнение ПФМ вместо x1. После очевидных преобразований получим второе уравнение структурной формы:
Окончательный вид структурной модели:
