Оценка влияния отдельных факторов на исследуемую переменную

Важную роль при оценке влияния отдельных факторов играют коэффициенты регрессионной модели a_j. Однако непосредственно с их помощью нельзя сопоставить факторы по степени их влияния на зависимую переменную из-за различия единиц измерения и разного масштаба колебаний (степени колеблемости) при использовании разных наборов результатов наблюдений.

Для устранения таких различий применяются частные коэффициенты эластичности:

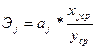, (3.10)

где 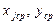- средние значения переменных в рядах наблюдений и бета - коэффициенты

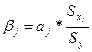, (3.11)

где 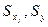- среднеквадратические отклонения переменных:

. (3.12)

Коэффициент эластичности показывает, на сколько процентов изменяется исследуемая переменная при изменении факторной переменной на 1 процент. Если коэффициент эластичности меньше 0, то при увеличении значения фактора исследуемая переменная уменьшается. Таким образом, коэффициенты эластичности можно сравнивать между собой по модулю для выяснения того, изменения какого фактора больше влияют на изменение исследуемой переменной. Однако коэффициент эластичности не учитывает степень колеблемости факторов.

Бета – коэффициент показывает, на какую часть величины среднеквадратического отклонения 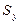изменится переменная y с изменением соответствующей независимой переменной x_j на величину своего среднеквадратического отклонения при фиксированном уровне значений остальных факторных переменных.

Указанные коэффициенты позволяют упорядочить факторы по степени их влияния на исследуемую переменную.

Долю влияния фактора в суммарном влиянии всех факторов можно оценить по величине дельта – коэффициентов:

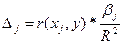, (3.13)

где 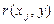- коэффициент парной корреляции между фактором x_j и исследуемой переменной y.

Рассчитаем значения коэффициентов эластичности, бета - и дельта – коэффициентов для уравнения регрессии (3.8), частично используя уже произведённые вычисления.

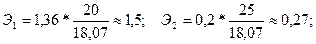
Таким образом, при увеличении температуры на 1% следует ожидать увеличения объёма продаж на 1,5%, а при увеличении торговой наценки на 1% ожидаемое увеличение объёма продаж составляет 0,27%.

Для определения бета – коэффициентов рассчитаем среднеквадратические отклонения:

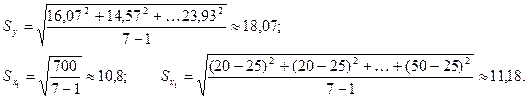
Тогда

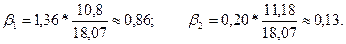
Значения бета – коэффициентов показывают, что при изменении x1 на одно своё среднеквадратическое отклонение значение y в среднем будет изменяться на 0,86 от своего среднеквадратического отклонения, а при изменении x2 на величину 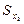значение у в среднем изменится на .

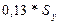Наконец, дельта – коэффициенты:

.

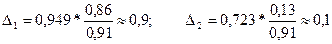Значения дельта – коэффициентов показывают, что доля влияния первого фактора составила 90%, а второго – 10%. Заметим, что сумма дельта – коэффициентов всегда равна 1. Этот факт можно использовать для проверки правильности произведённых вычислений.