Линейная регрессионная модель

Для анализа работы торгового предприятия произведено 10 наблюдений числа покупателей х_t и выручки y_t (табл.4):

Таблица 4
t
хt
yt

Предполагается, что зависимую переменную (выручку) и независимую (число покупателей в магазине) связывает линейное регрессионное уравнение .

1. Построим диаграмму рассеяния наблюдений (рис.1), откладывая на координатной плоско­сти 10 точек с координатами (31; 64), (75; 100),…, (21; 37):

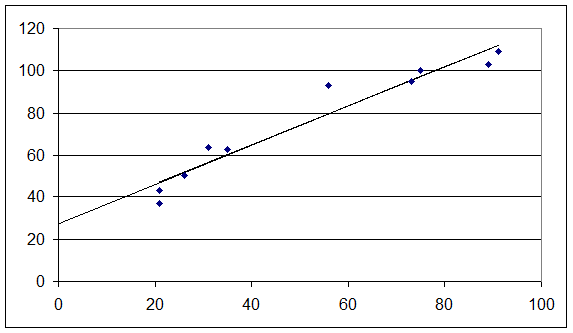
Рис.1 Диаграмма рассеяния наблюдений (точки), линейный тренд (сплошная прямая).

По типу диаграммы рассеяния можно предположить, что между наблюдениями х и у существует линейная зависимость.

2. Применяя метод наименьших квадратов, получим оценки параметров а и b линейной регрессионной модели:

Оценка параметра b вычисляется по формуле
,
где ; ; ; ;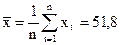
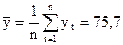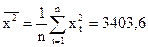n – число наблюдений. В представленном примере n=10.

Оценка параметра a вычисляется по формуле

.

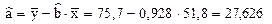Для получения оценок параметров модели удобно использовать табл.5:

Таблица 5
t	xt	yt		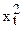	xtyt		et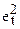
						56,396	7,604	57,817
						97,231	2,769	7,667
						110,224	-7,224	52,186
						51,756	-1,756	3,083
						60,109	2,891	8,361
						95,375	-0,375	0,141
						112,080	-3,080	9,487
						47,116	-4,116	16,938
						79,598	13,402	179,617
						47,116	-10,116	102,326
Σ						757,000	0,000	437,623
Σ/n	51,8	75,7	3403,6		4589,8	75,700	0,000

Можно сделать следующие выводы:

• среднее число покупателей 51,8;
• средняя выручка 75,7 ед.;
• каждый покупатель приносит в среднем 0,928 ед. выручки.

3. Уравнение прогнозных значений имеет вид:

.

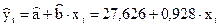Заполним соответствующий столбец в таблице и построим гра­фик прогнозных значений на диаграмме рассеяния.

4. Остатки линейной регрессионной модели определим по формуле

Оценка дисперсии остатков равна

.

Оценка дисперсии 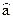равна

.

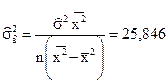Оценка дисперсии 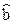равна

.

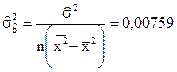5. Гипотеза будет проверяться исходя из того, что случайная величина

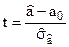
в нормальной классической линейной регрессионной модели подчиняется распределению Стьюдента с (n-2) степенями свободы. Если 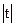окажется меньше некоторого критического значения t_α, которое находится по таблицам критических точек распределения Стьюдента, то гипотеза принимается. Если больше, то гипотеза от­вергается. Таблица критических точек распределения Стьюдента приводится в Приложении 1. По таблице находим, что для уровня значимости 0,05 и восьми степеней свободы

t_α=2,306.

Проверим нулевую гипотезу Н₀: а=0, при конкурирующей Н₁: 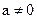. Вычислим

Поскольку 5,434>2,306, то нулевая гипотеза отвергается.

Выше сказанное справедливо и для параметра b. Проверим гипотезу b=1, которая означает, что один покупатель в среднем приносит торговой точке единицу выручки. Вычислим

.

Поскольку 0,826<2,306, то гипотеза принимается.

6. Из неравенств

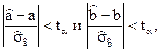
находим

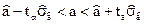
и

.

Подставляя найденные ранее значения, находим 95% доверительные интервалы

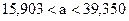и .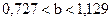

Последнее неравенство означает, что с вероятностью 0,95 средняя выручка, которую приносит один покупатель, принадлежит интервалу (0,727; 1,129).

7. Коэффициент детерминации равен отношению суммы квадратов отклонений регрессии к общей сумме квадратов отклонений:

.

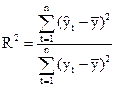Можно доказать, что для парной регрессии данное отношение равно

,

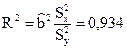где 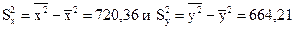выборочные дисперсии.

В построенной модели дисперсия результата на 93,4% объясняется линейной зависимостью выручки от числа покупателей и только на 6,6% дисперсией неучтенных факторов. Полученное значение коэффициента детерминации близко к единице. Поэтому связь между х и у сильная (число покупателей заметно влияет на выручку данного предприятия).

8. Если фактор (в нашей задаче число покупателей) не влияет на результат (выручку), тогда дисперсионное отношение

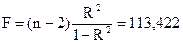
в классической нормальной линейной регрессионной модели, подчиняется распределению Фишера с (1; n-2) числом степеней свободы. По таблице критических точек распределения Фишера (Приложение 2) находим, что для уровня значимости α=0,05, величина F_α=10,128 (число степеней свободы: 1; 8). Найденное значение F>> F_α, что указывает на сильное влияние фактора на результат.

9. Допустим, что планируется расширение предприятия, при этом среднее количество покупателей должно вырасти на 20% и составит чел. Необходимо определить среднюю выручку, которую в этом случае получит предприятие. Выручку найдем из прогнозного уравнения

.

Определим, насколько точным является данный прогноз. Для этого построим 95% доверительный интервал для прогнозируемой выручки:

где 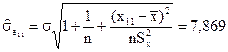- стандартное отклонение е₁₁.

10. Эластичность в произвольной точке определяется по формуле

,

где - производная по фактору х. В точке х₁₁ эластичность равна

.

Найденная величина означает, что при увеличении числа покупателей на 1% выручка возрастает в среднем на 0,692%. Справедливо это в окрестности точки х₁₁.