Способы описания алгоритмов.

Лекция 19

Тема: Алгоритмизация.

Время: 2ч.

Введение

Слово «алгоритм»содержит в своем составе преобразованное географическое название Хорезм. Термин «алгоритм» обязан своим происхождением великому ученому средневекового Востока - Мухаммеду ибн Мусе ал - Хорезми (Магомет, сын Моисея из Хорезма), жившего примерно в 783 - 850 гг. В латинских переводах с арабского арифметического трактата ал - Хорезми его имя транскрибировалось как algorismi. Откуда и пошло слово «алгоритм» - сначала для обозначения алгоритмов цифровых вычислений десятичной позиционной арифметики, а затем для обозначения произвольных процессов, в которых искомые величины последовательно определяются из исходных данных по определенным правилам - инструкциям.

Вплоть до 30-х годов нашего столетия понятие алгоритма оставалось интуитивным, имевшим скорее методологическое, чем математическое значение. К началу ХХ в. много ярких примеров алгоритмов дали алгебра и теория чисел.

Например, алгоритм Евклида нахождения наибольшего общего делителя двух натуральных чисел или двух целочисленных многочленов, алгоритм Гаусса решения системы линейных уравнений, алгоритм нахождения рациональных корней многочленов одного переменного с рациональными коэффициентами, алгоритм Штурма определения числа действительных корней многочлена с действительными коэффициентами на некотором отрезке действительных чисел, алгоритм разложения многочлена от одного переменного на неприводимые множители.

Данные алгоритмические модели отождествляются с формальным понятием алгоритма. Выделяются несколько основных типов алгоритмических моделей, различающиеся исходными трактовками того, что такое алгоритм:

1. Первый тип трактует алгоритм как некоторое детерминированное устройство, способное выполнять в каждый момент лишь строго фиксированное множество операций. Основные теоретические модели - машина Тьюринга, предложена им в 30-х годах, оказавшая существенное влияние на понимание логической природы разрабатываемых ЭВМ) и машина произвольного доступа (МПД), введена в 70-х годах с целью моделирования реальных вычислительных машин и получения оценок сложности вычислений.

2. Второй тип связывает понятие алгоритма с традиционным представлением - процедурами вычисления значений числовых функций. Основная теоретическая модель - рекурсивные функции.

3. Третий тип - это преобразования слов в произвольных алфавитах, в которых операциями являются замены кусков слов другим словом. Основная теоретическая модель - нормальные алгоритмы Маркова.

Теория алгоритмов оказала существенное влияние на развитие ЭВМ и практику программирования. В теории алгоритмов были предугаданы основные концепции, заложенные в аппаратуру и языки программирования ЭВМ. Например, микропрограммирование строится на идеях машин Тьюринга, структурное программирование заимствовало свои конструкции из теории рекурсивных функций, языки символьной обработки информации (РЕФАЛ, ПРОЛОГ) берут начало от нормальных алгоритмов Маркова и систем Поста.

Понятие алгоритма.

Алгоритм -это понятное и точное предписание (инструкция) исполнителю выполнить конечную последовательность действий (команд), приводящих от исходных данных к искомому результату.

Пример: Вычислить значение Y(X) по формуле: Y(X) = (АХ + В) * (СХ - D)

1) А умножить на Х (АХ = R1) → R1;

2) R1сложить с В (R1+В = AX+B) → R2;

3) С умножить наХ (СХ = R3) → R3;

4)из R3вычестьD (R3 – D = CX - D) →R4;

5) R2 умножить R4 (R2*R4 = (AX+B)*(CX-D) = Y(X)) → Y(X).

Это предписание является алгоритмом для решения поставленной задачи. Для человека, выполняющего действие, необязательно знать исходную формулу, а достаточно следовать данному предписанию, исполняя все пункт за пунктом. С помощью алгоритмов можно решать не только вычислительные, но и другие задачи.

Исполнитель алгоритма – некоторая абстрактная или реальная (техническая, биологическая или биотехническая) система, способная выполнить действия, предписываемые алгоритмом.

Исполнителя характеризуют:

1. Среда (обстановка) – «место обитания » исполнителя, а также состояние среды.

2. Система команд – команды некоторого заданного списка для исполнителя, где

по выполнению описывается достижения результат.

3. После вызова команды исполнитель совершает определенные элементарные

Действия.

4. Отказы исполнителя возникают, если команда вызывается при недопустимом для

нее состоянии среды.

Свойства алгоритмов.

1) Точность -на каждом этапе алгоритма точно известно, что нужно делать

2) Дискретность –каждый шаг алгоритма должен указывать только одно конкретное действие и исполнитель должен выполнять его целиком.

3) Массовость –с помощью одного алгоритма можно решать однотипные задачи и делать это неоднократно.

4) Конечность– результат достигается за конечное число шагов.

5) Результативность –исполнение алгоритма приводит к решению задачи (один из вариантов задачи решения не имеет).

Пример:Построить график функции Y(x) = a | x |, где a > 0

1)Начертить график функции Y(x) = а x, а > 0;

2)Стереть часть графика, находящейся левее оси ординат (OY);

3) Симметрично отобразить оставшуюся часть графика относительно оси ординат (OY).

Y Y

Y(x) = ax О О Y(x) = a | x |

X Х

Нач

еслиa < b тоy: = aиначе y: = b

Все: конец.

4. Графический –в виде блоков. Каждый блок на этой схеме изображается

некоторой геометрической фигурой, различных по типу выполняемых

действий блокам соответствуют различные геометрические фигуры.

Типы алгоритмов.

Алгоритмы делятся на три группы: линейные, разветвляющие и циклические.

1. Линейный –алгоритм, в котором все этапы решения задачи выполняются строго последовательно, друг за другом, по одному разу.

Схематически линейный алгоритм изображается следующим образом:

2. Разветвляющий – алгоритм, в котором выбирается один из существующих возможных путей вычислительного процесса. Каждый такой путь называется ветвью алгоритма.

Разветвляющий алгоритм схематически изображается так:

Примеры построения блок - схем.

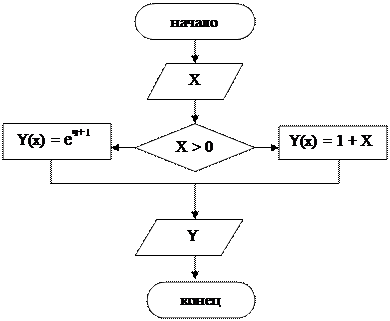
Пример 5.1. Составить алгоритм нахождения значения функции: Y(x) = x² + 1.

В данном задании можно проследить признаки линейного типа

Алгоритма.

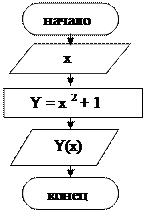Прежде чем строить блок - схему для данного

задания, необходимо записать по шагам на

алгоритмическом языке, как будет вычисляться

значение данной функции.

1. начало;

2. ввод переменной x;

3. Y(x) = x² + 1;

4. вывод Y(x);

5. конец.

Пример 5.2. Вывести на печать наибольшее из двух произвольных чисел A и B (A ≠ B).

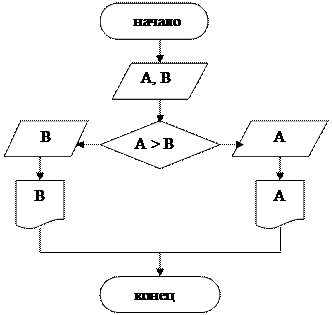В данном задании прослеживаются признаки

разветвляющего типа алгоритма, т.к. явно

видно, что присутствует условие, которое

скрывается под сравнением (наибольшее

Задания.

УПРАЖНЕНИЕ 1: Решение задач по типам алгоритмов.

Цель: закрепление и достижение прочности знаний по конструированию

схем алгоритма.

1. Даны функции y = x² + 1, y = Sin x + BD, y = 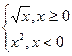, аргумент х = 4.5, а переменные B и D – произвольные. Построить блок – схему данных функциональных зависимостей.

2. Вывести на принтер наибольшее из двух любых чисел А и В (А ≠ В).

3. Задана последовательность чисел 3,5,7,…,21.Составить блок-схему вывода суммы всех элементов.

4. Составить блок-схему поиска значений большей из трех величин А, В, С.

5. Составить алгоритм вычисления периметра и площади прямоугольного треугольника, у которого длина одного катета в 2 раза больше длины другого, а длина гипотенузы с (a, b -катеты).

УПРАЖНЕНИЕ 2: Решение задач по разветвляющемуся и циклическому типу

алгоритма.

Цель: закрепление навыков конструирования логических схем по разветвляющему

и циклическому типу алгоритма.

1. Составить алгоритм нахождения значения следующих функций:

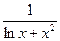y = , y =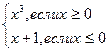

2. Вычислить значение функции y = x² + bx + c при x 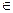[2;6], ∆x = 2.

3. Составить алгоритм вычисления функциональной зависимости

y (x) =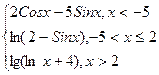

4. Вычислить значение функции y = 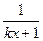для k 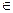[1;100], ∆k= 1.

5. Вычислить значение функции Y = k x + P для P значений с заменой вместо P на 100.

УПРАЖНЕНИЕ 3: Циклические алгоритмы с одним циклом.

Цель: закрепление навыков построения логических схем по циклическому типу

алгоритма.

1. Вычислить значение f(x) = x Sin(1 - (cos x + tg x)) для значений x [–15;15], ∆ х = 0,15.

2. Составить алгоритм нахождения площади равнобедренного треугольника, значение высоты которого равна Н, длина основания – а, а длина катета в 2 раза больше длины основания.

3. Составить алгоритм вычисления значения функциональной зависимости

ξ (x) = 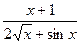для значений x (A; B) с шагом t.

4. Составить блок – схему функциональной зависимости f(x)=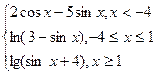

5. Вычислить значение ψ (x) = 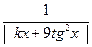для 10 произвольно заданных значений переменной x.

УПРАЖНЕНИЕ 4: Циклические алгоритмы с одним циклом.

Цель: закрепление навыков построения логических схем по циклическому типу

алгоритма.

1. Составить алгоритм вычисления следующих функций: f (x) = 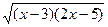; y (x) = 3Sin ( 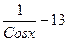); ω(x) = x Tg (x-1) + arcSin²(x).

2. Найти сумму целых положительных чисел, кратных 4 и меньших 100. Построить блок – схему вычисления суммы.

3. В компьютер поступают результаты соревнований по плаванью для 3 спортсменов. Составить алгоритм, который выбирает наилучший результат с сообщением результата победителя.

4. Дана последовательность чисел {X_n}= 1,2,3,…10. Найти среднее арифметическое четных чисел данной последовательности.

5. Составить алгоритм нахождения факториала числа n! и суммы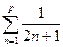

8. Дополнительные задания.

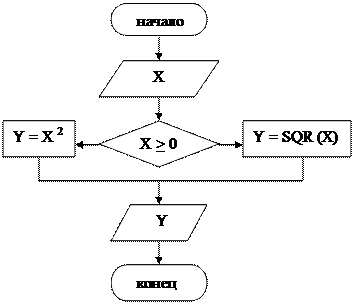
1. По данным схемам записать исходные данные и описание на алгоритмическом языке.

a) Схема № 1. b) Схема № 2.

- +

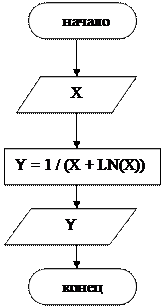С) Схема № 3.

- +

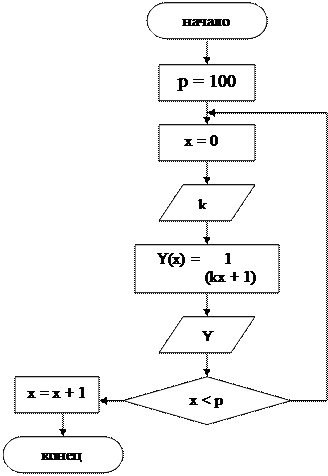d) Схема № 4. е) Схема № 5.

+ -

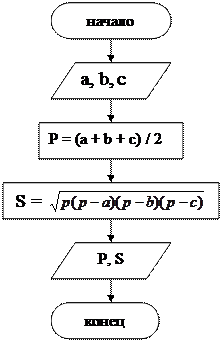2. По аналитической записи изобразить блок - схему и записать исходную формулу с указанным условием.

а) Аналитическая запись № 1. b) Аналитическая запись № 2.

1. начало 1. начало;

2. b = 10; 2. ввод a, b, с, R;

3. x = 0; 3. S = (abc)/4R;

4. x = x +1; 4. вывод S;

5. ввод k; 5.конец.

6. Y(x) = (x + b)/(x +1);

7. вывод Y;

8. если x < b, то перейти к 3.;

9. конец.

с) Аналитическая запись № 3. d) Аналитическая запись №4.

1. начало; 1. начало;

2. ввод x; 2. ввод A, B, t;

3. если x > 0, то Y(x) = 1/(2 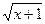); 3. x = A;

иначе Y(x) = | 2x - 1 |; 4. Y(x) = x³;

4. вывод Y(x); 5. вывод Y(x);

5. конец. 6. x = x + t;

7. если x < B, то перейти 4.;

8. конец.

Лекция 19

Тема: Алгоритмизация.

Время: 2ч.

Введение

Слово «алгоритм»содержит в своем составе преобразованное географическое название Хорезм. Термин «алгоритм» обязан своим происхождением великому ученому средневекового Востока - Мухаммеду ибн Мусе ал - Хорезми (Магомет, сын Моисея из Хорезма), жившего примерно в 783 - 850 гг. В латинских переводах с арабского арифметического трактата ал - Хорезми его имя транскрибировалось как algorismi. Откуда и пошло слово «алгоритм» - сначала для обозначения алгоритмов цифровых вычислений десятичной позиционной арифметики, а затем для обозначения произвольных процессов, в которых искомые величины последовательно определяются из исходных данных по определенным правилам - инструкциям.

Вплоть до 30-х годов нашего столетия понятие алгоритма оставалось интуитивным, имевшим скорее методологическое, чем математическое значение. К началу ХХ в. много ярких примеров алгоритмов дали алгебра и теория чисел.

Например, алгоритм Евклида нахождения наибольшего общего делителя двух натуральных чисел или двух целочисленных многочленов, алгоритм Гаусса решения системы линейных уравнений, алгоритм нахождения рациональных корней многочленов одного переменного с рациональными коэффициентами, алгоритм Штурма определения числа действительных корней многочлена с действительными коэффициентами на некотором отрезке действительных чисел, алгоритм разложения многочлена от одного переменного на неприводимые множители.

Данные алгоритмические модели отождествляются с формальным понятием алгоритма. Выделяются несколько основных типов алгоритмических моделей, различающиеся исходными трактовками того, что такое алгоритм:

1. Первый тип трактует алгоритм как некоторое детерминированное устройство, способное выполнять в каждый момент лишь строго фиксированное множество операций. Основные теоретические модели - машина Тьюринга, предложена им в 30-х годах, оказавшая существенное влияние на понимание логической природы разрабатываемых ЭВМ) и машина произвольного доступа (МПД), введена в 70-х годах с целью моделирования реальных вычислительных машин и получения оценок сложности вычислений.

2. Второй тип связывает понятие алгоритма с традиционным представлением - процедурами вычисления значений числовых функций. Основная теоретическая модель - рекурсивные функции.

3. Третий тип - это преобразования слов в произвольных алфавитах, в которых операциями являются замены кусков слов другим словом. Основная теоретическая модель - нормальные алгоритмы Маркова.

Теория алгоритмов оказала существенное влияние на развитие ЭВМ и практику программирования. В теории алгоритмов были предугаданы основные концепции, заложенные в аппаратуру и языки программирования ЭВМ. Например, микропрограммирование строится на идеях машин Тьюринга, структурное программирование заимствовало свои конструкции из теории рекурсивных функций, языки символьной обработки информации (РЕФАЛ, ПРОЛОГ) берут начало от нормальных алгоритмов Маркова и систем Поста.

Понятие алгоритма.

Алгоритм -это понятное и точное предписание (инструкция) исполнителю выполнить конечную последовательность действий (команд), приводящих от исходных данных к искомому результату.

Пример: Вычислить значение Y(X) по формуле: Y(X) = (АХ + В) * (СХ - D)

1) А умножить на Х (АХ = R1) → R1;

2) R1сложить с В (R1+В = AX+B) → R2;

3) С умножить наХ (СХ = R3) → R3;

4)из R3вычестьD (R3 – D = CX - D) →R4;

5) R2 умножить R4 (R2*R4 = (AX+B)*(CX-D) = Y(X)) → Y(X).

Это предписание является алгоритмом для решения поставленной задачи. Для человека, выполняющего действие, необязательно знать исходную формулу, а достаточно следовать данному предписанию, исполняя все пункт за пунктом. С помощью алгоритмов можно решать не только вычислительные, но и другие задачи.

Исполнитель алгоритма – некоторая абстрактная или реальная (техническая, биологическая или биотехническая) система, способная выполнить действия, предписываемые алгоритмом.

Исполнителя характеризуют:

1. Среда (обстановка) – «место обитания » исполнителя, а также состояние среды.

2. Система команд – команды некоторого заданного списка для исполнителя, где

по выполнению описывается достижения результат.

3. После вызова команды исполнитель совершает определенные элементарные

Действия.

4. Отказы исполнителя возникают, если команда вызывается при недопустимом для

нее состоянии среды.

Свойства алгоритмов.

1) Точность -на каждом этапе алгоритма точно известно, что нужно делать

2) Дискретность –каждый шаг алгоритма должен указывать только одно конкретное действие и исполнитель должен выполнять его целиком.

3) Массовость –с помощью одного алгоритма можно решать однотипные задачи и делать это неоднократно.

4) Конечность– результат достигается за конечное число шагов.

5) Результативность –исполнение алгоритма приводит к решению задачи (один из вариантов задачи решения не имеет).

Пример:Построить график функции Y(x) = a | x |, где a > 0

1)Начертить график функции Y(x) = а x, а > 0;

2)Стереть часть графика, находящейся левее оси ординат (OY);

3) Симметрично отобразить оставшуюся часть графика относительно оси ординат (OY).

Y Y

Y(x) = ax О О Y(x) = a | x |

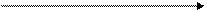
X Х

Способы описания алгоритмов.

Известно три основных способа записи алгоритмов:

1. Словесный - используется на начальных этапах изучения алгоритмов и предназначен для исполнения алгоритма человеком. Форма записи команд произвольная, главное, чтобы был понятным и точным.

2. Программная –тексты на языках программирования.

3. Псевдокоды – описание на алгоритмическом языке.

Алгоритмический язык– это средство для записи алгоритмов в аналитическом виде, промежуточном между записью алгоритма на естественном языке и записью на языке ЭВМ.

Пример: алгминимальное из двух чисел

аргa, b; резy

Нач

еслиa < b тоy: = aиначе y: = b

Все: конец.

4. Графический –в виде блоков. Каждый блок на этой схеме изображается

некоторой геометрической фигурой, различных по типу выполняемых

действий блокам соответствуют различные геометрические фигуры.