Системы линейных алгебраических уравнений
Система вида
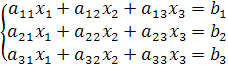
называется системой линейных уравнений с тремя неизвестными:
Система, имеющая хотя бы одно решение, называется совместной, а система, не имеющая ни одного решения, - несовместной.
Определитель
∆ = 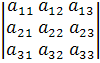 ,
,
составленный из коэффициентов при неизвестных, называется определителем системы.
Линейная система называется невырожденной, если её определитель не равен нулю.
Невырожденная линейная система имеет единственное решение, которое определяется по формулам Крамера:
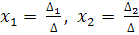 ,
, 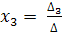 ,
,
где ∆1, ∆2, ∆3 - определители, получаемые из определителя ∆ путем замены его первого, второго, третьего столбцов столбцом свободных членов.
Если ∆ = 0, а один из определителей ∆1, ∆2, ∆3 ≠ 0, то система не имеет решения.
Если ∆ = ∆1 = ∆2 = ∆3 = 0, то система имеет множество решений.
Формулы Крамера используются и при решении системы п линейных уравнений с п неизвестными.
Пример 2.5. Решить систему уравнений по формулам Крамера:
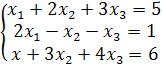
Решение
Вычислим определители:
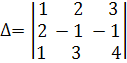 = 1 .
= 1 . 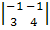 - 2 .
- 2 . 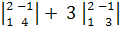 = 2.
= 2.
Т. к. определитель системы ∆ = 2 ≠ 0, то система имеет единственное решение.
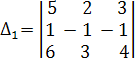 = 5 .
= 5 . 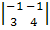 - 2 .
- 2 . 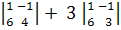 = 2,
= 2,
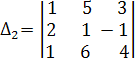 = 1 .
= 1 . 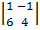 - 5 .
- 5 . 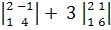 = - 2,
= - 2,
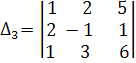 = 1 .
= 1 . 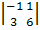 - 2 .
- 2 . 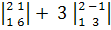 = 4.
= 4.
По формуле Крамера:
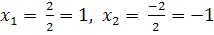 ,
, 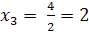 .
.
Ответ: (1; - 1; 2)
Пусть требуется решить систему п линейных уравнений с п неизвестными
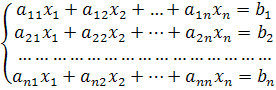
Наиболее распространенным методом решения системы линейных уравнений является алгоритм последовательного исключения неизвестных, который называется методом Гаусса. Согласно этому методу составляется соответствующая данной системе расширенная матрица и приводится к треугольному виду путем проведения преобразований над ее строками.
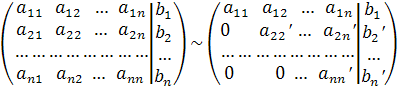
По полученной матрице составляется система линейных уравнений, решить которую не представляет трудности. Продемонстрируем данный метод на конкретных примерах.
Пример 2.6. Решить систему линейных уравнений методом Гаусса:
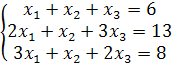
Решение
Запишем расширенную матрицу системы и преобразуем её:
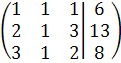
К элементам второй строки прибавим соответствующие элементы первой строки, умноженные на (-2). К элементам третьей строки прибавим соответствующие элементы первой строки, умноженные на (-3).
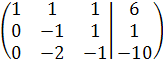
К элементам третьей строки прибавим соответствующие элементы второй строки, умноженные на (-2).
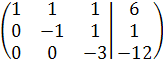
Оформим проведенные преобразования в виде:
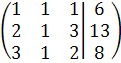
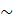
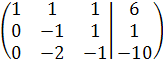
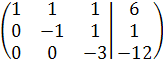
Полученной матрице соответствует система линейных уравнений:
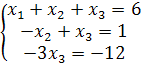 ⇔
⇔ 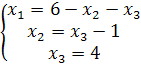 ⇔
⇔ 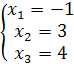
Ответ: (-1; 2; 3)
Пример 2.7.Решить систему линейных уравнений методом Гаусса:
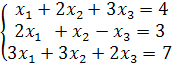
Решение
Запишем расширенную матрицу системы и преобразуем её:
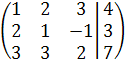
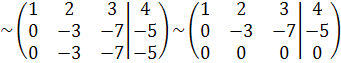
Запишем соответствующую полученной матрице систему. Зафиксировав х3 , выразим х2 ,х1:
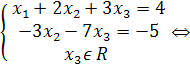
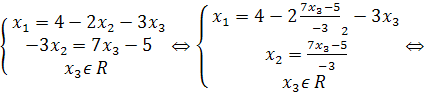
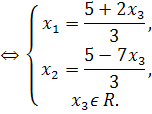
Ответ: ( 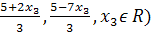
Контрольные вопросы
1. Что называется матрицей?
2. Какая матрица называется квадратной?
3. Как определяется порядок матрицы?
4. Какая матрица называется треугольной?
5. Какие элементарные преобразования можно производить над матрицами?
6. Назовите линейные операции над матрицами.
7. Что называется определителем первого прядка?
8. Что называется главной диагональю определителя?
9. Что называется побочной диагональю определителя?
10. Что представляет собой определитель второго порядка?
11. Как вычисляется определитель третьего порядка?
12. Какая система линейных уравнений называется совместной? Несовместной?
13. Какая линейная система называется невырожденной?
14. Что представляет собой определитель системы линейных уравнений?
15. Что представляют собой формулы Крамера для решения систем линейных уравнений?
16. В чём заключается метод Гаусса решения линейной системы?
Практическое занятие № 1 (2часа)
