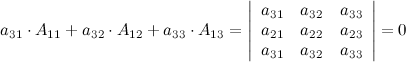Понятие определителя матрицы

Определение

Квадратной матрице 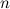-го порядка ставиться в соответствие число , называемое определителем матрицы или детерминантом.

Свойства определителей:

Замечание

Все что будет сказано относительно строк, будет относиться и к столбцам.

1° При транспонировании квадратной матрицы её определитель не меняется: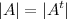

Пример

Известно, что определитель матрицы 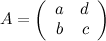равен 3. Тогда определитель матрицы 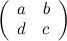, которая равна 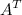, также равен 3.

2° Общий множитель в строке можно выносить за знак определителя.

Пример

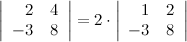
3°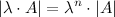

То есть, если квадратная матрица 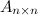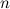-го порядка умножается на некоторое ненулевое число 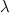, то определитель полученной матрицы равен произведению определителя исходной матрицы на число 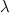в степени, равной порядку матриц.

Пример

Задание. Пусть определитель матрицы третьего порядка равен 3, вычислить определитель матрицы .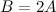

Решение. По свойству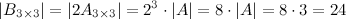

Ответ.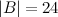

4° Если каждый элемент в какой-то строке определителя равен сумме двух слагаемых, то исходный определитель равен сумме двух определителей, в которых вместо этой строки стоят первые и вторые слагаемые соответственно, а остальные строки совпадают с исходным определителем.

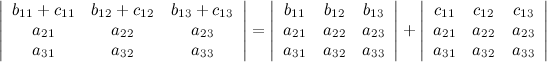
5° Если две строки определителя поменять местами, то определитель поменяет знак.

Пример

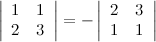
6° Определитель с двумя равными строками равен нулю.

Пример

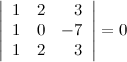
7° Определитель с двумя пропорциональными строками равен нулю.

Пример

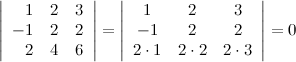
8° Определитель, содержащий нулевую строку, равен нулю.

Пример

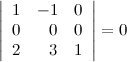
9° Определитель не изменится, если к какой-то его строке прибавить другую строку, умноженную на некоторое число.

Пример

Пусть задан определитель третьего порядка 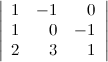. Прибавим ко второй строке определителя третью его строку, при этом значение определителя не измениться:

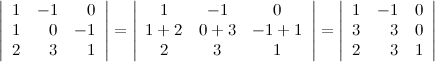
10° Определитель верхней (нижней) треугольной матрицы равен произведению его диагональных элементов.

Пример

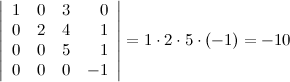
11° Определитель произведения матриц равен произведению определителей: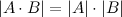

Минор и алгебраическое дополнение

Минор

Определение

Минором 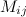к элементу 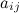определителя 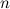-го порядка называется определитель 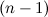-го порядка, полученный из исходного вычеркиванием 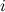-той строки и 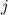-того столбца.

Пример

Задание. Найти минор 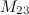к элементу 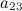определителя .

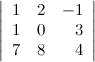Решение. Вычеркиваем в заданном определителе вторую строку и третий столбец:

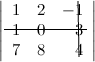
тогда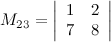

Ответ.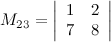

Алгебраическое дополнение

Определение

Алгебраическим дополнением 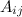к элементу 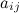определителя 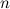-го порядка называется число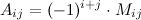

Пример

Задание. Найти алгебраическое дополнение 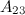к элементу 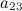определителя .

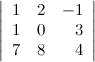Решение.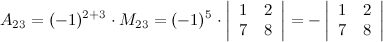

Ответ.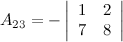

Сумма произведений элементов "произвольной" строки на алгебраические дополнения к элементам 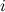-ой строки определителя равна определителю, в котором вместо 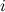-ой строки записана "произвольная" строка.

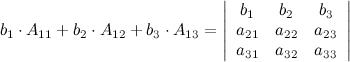
Сумма произведений элементов строки определителя на алгебраические дополнения к элементам другой строки равна нулю.