Реализация операционных устройств вычислительной машины.

Тип ОПБ магистрального ОПУ определяется способом обработки данных.

Различают ОПБ последовательного и параллельного типа. В первом случае операции осуществляются последовательно над всеми разрядами, побитно поступающими на входы ОПБ. Бит переноса, возникающий при этом, учитывается при обработке следующего разряда операнда. Результат побитно заносится в выходной регистр, предыдущее значение которого сдвигается на один разряд. За n циклов в выходном регистре формируется слово результата, где каждый разряд занимает предназначенную для него позицию. Во втором случае операции над всеми разрядами операнда осуществляются побитно параллельно. На практике часто используют альтернативный параллельно-последовательный вариант, при котором слово разбивается на группы (по 2, 4 или 8) разрядов, обработка этих разрядов внутри группы осуществляется параллельно, а сами группы обрабатываются последовательно.

Для большинства современных ВМ общепринятым является формат данных с ФЗ. По этой причине, соответствующие ОПУ называют целочисленными, обеспечивающие сложение/вычитание, умножение и деление. При выполнении операций сложения возможна ситуация, когда при сложении двух n разрядных чисел получается число разрядностью n+1 (переполнение). ОПУ должно выявлять факт переполнения и сигнализировать о нем. Обычно это организуется выставлением определенного флага в статусном регистре.

Чтобы облегчить обнаружение переполнения применяется модифицированный дополнительный код, когда для хранения знака отводится два разряда, причем оба участвуют в арифметической операции наравне с цифровыми разрядами. Когда переполнение отсутствует, оба знаковых разряда содержат одинаковое значение (оба 0 или 1). Различие же в знаковых разрядах говорит о возникновении переполнения.

Умножение является более сложной операцией. В современных ОПУ умножение реализуется по разному. В частности, имеют место алгоритмы со сдвигом. В общем случае, алгоритм сводится к формированию частичных произведений (ЧП), по одному на каждую цифру множителя, с последующим суммированием полученных ЧП. Перед суммированием каждое ЧП должно быть сдвинуто на один разряд относительно предыдущего. Перемножение двух n-разрядных чисел приводит к получению 2n-битного результата. Согласно этому алгоритму в устройстве умножения предполагается наличие множимого, множителя и суммы ЧП, а также сумматора и, возможно, схем сдвига. Средиосновных, различают два варианта умножения:

• со сдвигом суммы ЧП вправо при неподвижном множимом, начиная умножение с младших разрядов множителя (алгоритм сдвига вправо),
• со сдвигом суммы ЧП влево при неподвижном множимом, начиная умножение со старших разрядов множителя (алгоритм сдвига влево).

Суть алгоритма умножения со сдвигом вправо в следующем:

1. полное значение суммы ЧП полагается равным нулю,

2. анализируется очередная цифра множителя (анализ начинается с младшей цифры).

Если она равна единице, то к сумме частичных произведений прибавляется множимое, в противном случае прибавление не производится,

3. выполняется сдвиг суммы ЧП вправо на один разряд,

4. пункты 2 и 3 выполняются последовательно для всех цифровых разрядов множителя.

Схема аппаратной реализации приведена на Рисунок 2. Первоначально множимое и множитель заносятся в соответствующие регистры РМн. и РМт. Все разряды суммы ЧП устанавливаются в нуль. Умножение проходит за n-шагов, где n − количество разрядов множителя. На каждом шаге в зависимости от состояния младшего разряда множителя, который управляет мультиплексором, на один извыходом n-разрядного сумматора подается либо множимое, либо 0. На второй вход поступает содержимое регистра, используемого для хранения суммы ЧП.

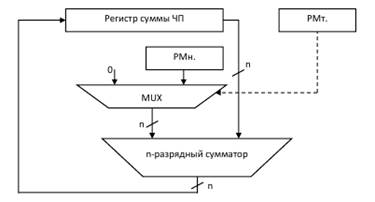
Рисунок 2 - Алгоритм умножения с правым сдвигом

Несколько сложнее обстоит дело с умножением чисел со знаком. Проблема в том, ОПУ выполняют операции над знаковыми разрядами также как и над числовыми. Если же знаковые разряды выделить специальным образом, то определение знака результата возможно при помощи логических функций.

Для ускорения умножения могут быть использованы логические и аппаратные методы. Логические методы позволяют уменьшить количество сложений в ходе умножения, а также обеспечить обработку нескольких разрядов за один шаг. Аппаратные способы ускорения умножения основаны на распараллеливании отдельных операций. Это приводит к существенному усложнению аппаратуры и как следствие возрастанию ее стоимости.

Рассмотрим вопрос о реализации базовых операций для данных с ПЗ. Они существенным образом отличаются от операций с ФЗ. Поэтому их как правило реализуют на базе отдельного ОПУ. Как минимум, это устройство должно реализовывать выполнение четырех арифметических действий: сложения, вычитания, умножения и деления.

Представление данных в формате с ПЗ полагает трехкомпонентное представление числа. Во-первых, речь идет о его знаке, во-вторых, о нормализованной мантиссе и, в третьих, о порядке числа. В силу этого, ОПУ состоят из трех соответствующих компонент: блока обработки знаков (БОЗ), блока обработки порядков (БОП) и блоков обработки мантисс (БОМ). Для хранения операндов и результата в ОПУ предусмотрены отдельные регистры. На подготовительном этапе операций с ПЗ осуществляется его разбиение на три составляющие. На этом этапе выполняется проверка на равенство нулю отдельных операндов. Это позволяет в дальнейшем исключить лишние операции. Действия на заключительном этапе выполнения операций с ПЗ идентичны и сводятся к проверке нулевого значения мантиссы, ее нормализации.

Сложение (вычитание) чисел с ПЗ состоит из следующих этапов:

• подготовительный этап,
• определение операнда, имеющего меньший порядок, и сдвиг его мантмссы вправо на число разрядов, равное разности порядков,
• приравнивание порядка результата большему из порядков операндов,
• сложение или вычитание мантисс и определение знака результата,
• проверка на переполнение,
• заключительный этап.

При выполнении умножения (или деления) на предварительном этапе осуществляется проверка на нуль одного из сомножителей, что позволяет сразу выдать результат или сообщение об ошибке. Далее выполняется сложение (или вычитание) порядков. Если порядок выходит за допустимые границы (переполнение порядка или потеря значимости), то выдается соответсвующее сообщение об ошибке. Операции над порядками осуществляются также как и операции в целочисленной арифметике. Затем идут операции над мантиссами (перемножение / деление) как с числами с ФЗ, которые завершаются операциями округления, нормализации и компоновки результата.