Математическая модель нейрона

Множество математических моделей нейрона может быть построено на более простой концепции строения нейрона. На рис.6.3. показана наиболее общая схема. Так называемая суммирующая функция объединяет все входные сигналы , которые поступают от нейронов-отправителей. Значением такого объединения является взвешенная сумма, где веса 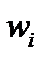представляют собой синаптические мощности. Возбуждающие синапсы имеют положительные веса, а тормозящие синапсы-отрицательные веса. Для выражения нижнего уровня активности нейронак взвешенной сумме прибавляется компенсация (смещение) .

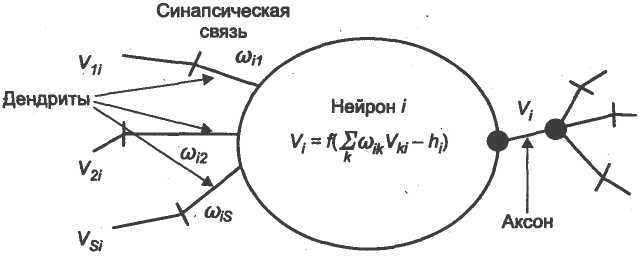
Рис.6.3. Простая математическая модель нейрона.

Так называемая функция активации рассчитывает выходной сигнал нейрона

по уровню активности 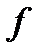. Функция активации обычно является сигмоидальной, как показано в правой нижней рамке на рис. 6.4. Другими возможными видами функций активации являются линейная и радиально-симметричная функции, показанные на рис. 6.4.

Рис. 6.4. Функции активации нейронов (возбуждение выходного слоя):

Здесь: а-область возбуждения букв; б-область возбуждения цифр; в- область

возбуждения специальных знаков.

Обучение нейронных сетей

Существует множество способов построения нейронных сетей. Они различаются своей архитектурой и методами обучения.

Первый шаг в проектированиинейронной сети состоит в ее обучении желаемому поведению. Это-фаза обучения. Для этого используется так называемая обучающая выборка или учитель. Учитель-это либо математическая функция, либо лицо, которое оценивает качество поведения нейронной сети. Поскольку нейронные сети в основном используются в сложных применениях, где нет хороших математических моделей, то обучение производится с помощью обучающей выборки, то есть эталонных пар «входы-выходы».

После завершения обучения нейронная сеть готова к использованию. Это-рабочая фаза. В результате обучения нейронная сеть будет вычислять выходные сигналы, близкие к эталонным данным при соответствующих входных сигналах. При промежуточных входных сигналах сеть аппроксимирует необходимые выходные величины. Поведение нейронной сети в рабочей фазе детерминировано, то есть каждой комбинации входных сигналов на выходе будут одни и те же сигналы. На протяжении рабочей фазы нейронная сеть не обучается. Это очень важно для большинства технических применений, поскольку система не будет стремиться к экстремальному поведению [91].

Собаки Павлова.Как же обучается нейронная сеть? Как правило,это демонстрируется на примере известных собак Павлова. Когда он показывал собакам еду, у них выделялась слюна. В собачьих клетках устанавливались звонки. Когда звонил звоночек, у собак не выделялась слюна, т.е. они не видели разницу между звонком и едой. Тогда Павлов стал обучать собак иначе, каждый раз используя звоночек при предъявлении пищи. После этого, даже при отсутствии еды, наличие звоночка вызывало у собак слюну.

На рис. 6.5. показано, как простая модель нейрона может быть представлена на примере «собаки Павлова». Имеется два входных нейрона: один из них соответствует тому, что собака видит пищу, другой-наличию звонка. Оба входных нейрона имеют связи с выходным нейроном. Эти связи соответствуют синапсам, а толщина линий-весам синапсов. Перед обучением собака реагирует лишь на еду, но не на звонок. Следовательно, линия между входным и выходным нейронами являетсяжирной, в то время как линия между правым входным и выходным нейронами является очень толстой.

Рис. 6.5. Принцип «эксперимента Павлова» над собаками: моделирование

реакции на изображение.

Правило обучения Хебба.Совершенно очевидно, что звонок при предъявлении пищи вырабатывает ассоциацию между ним и едой. Следовательно, выходная линия также становится толще, поскольку увеличивается вес синапса. На результатах этих наблюдений Хебб [81] в 1949 году предложил следующее обучающее правило: Увеличивать вес активного входа нейрона, если выход этого нейрона может быть активным. Уменьшить вес активного входа нейрона, если выход этого нейрона не может быть активным.

Это правило, названное правилом Хебба, предшествует всем обучающим правилам, включая наиболее используемый в настоящее время метод обратного распространения ошибки (errorbackpropagationalgorithm) [81].