Влияние погрешностей исходных данных на погрешности диагноза

Анализ влияния погрешностей измеряемых параметров на конечный диагноз выполняется с помощью следующей модели, использующей метод Лагранжа Ж.-Л. и (3.43), т.е.

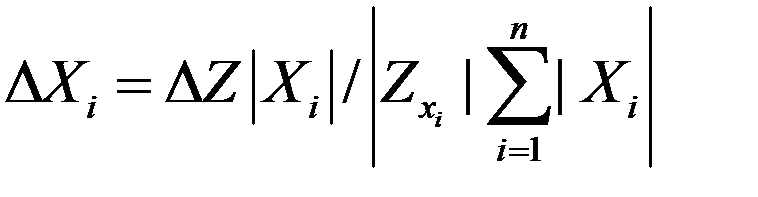. (3.48)

Для устранения разнозначных погрешностей и выполнения «согласования балансов», аналогично [72], вводим в (3.48) так называемые «регуляризующие добавки» , которые позволят привести приведенную погрешность конечной функции близко к 1%. Тогда (3.48) будет иметь вид:

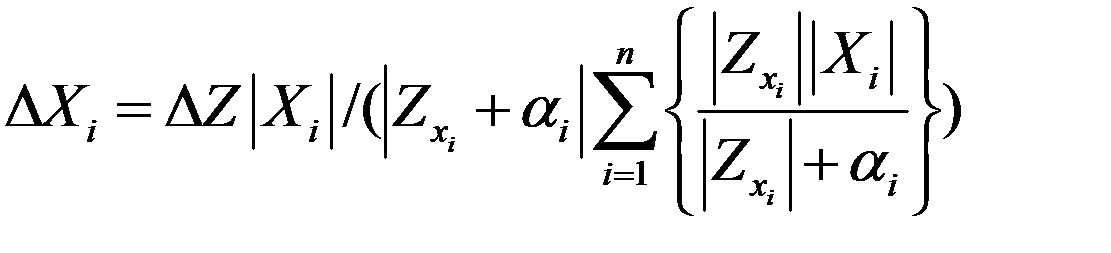. (3.49)

Подставляя (3.49) в выражение (3.47), получим, после преобразований, целевую функцию корректирования погрешностей и согласования балансов:

. (3.50)

Функция (3.50) решается, при обязательном выполнении условия (3.43) с помощью методов оптимизации из модуля программно-диагностического комплекса SKAIS.

Итак, решение задачи технической диагностики энергоустановки (или любого другого непрерывно действующего агрегата) выполняется на основе ее математического описания в виде граф – модели. В алгоритм решения задачи выбора диагностических параметров положены методы оценки параметров, по их информативности и доступности, определение веса дуг и вершин граф – модели механизма энергоустановки.

Для решения задач технического обслуживния используется специально разработанный автором программный комплекс SKAIS (рис. 3.5) с модулем OPTIMIZATOR (рис. 3.9).

OPTIMIZATOR подсистемы диагностики состояния энергоустановок SKAIS

Диагностический контроль энергоустановок тепловой электростанции (ТЭС) осуществляется с помощью экспертной диагностической системы функционально-гибридного типа с именем SKAIS. SKAIS - «Система контроля, анализа и слежения за изменением состояния энергоустановки» - управляемый в диалоговом режиме программный комплекс, ориентированный на диагностирование и экспертизу энергоустановок любых типов. SKAIS позволяет на ранней стадии (с использованием экспресс - испытаний) диагностировать снижение экономичности, определять величину, причины и опасность происходящих изменений, прогнозировать состояние, оценивать надежность, остаточный ресурс, долговечность, степень риска и ущерб от продолжения дальнейшей эксплуатации энергоустановки. Система SKAIS выполняет принятие решений на выход из создавшейся конфликтной ситуации (вывод в ремонт или введение ограничения) с представлением подготовленных в базе знаний рекомендаций (в виде готовых продукций - решающих правил) оперативному и ремонтному персоналу тепловой электростанции. Для этого создается база данных и знаний (БД и З) обо всех вынужденных остановах и дефектах оборудования, отклонениях от правил его нормальной эксплуатации.

Объяснение

В интеллектуальном центре подсистемы контроля и диагностики энергоустановок ТЭС – работает программный модуль по схеме . Основное назначение модуля – программное решение задач минимизации функций цели, имеющих несколько минимумов, но достаточно гладких в окрестностях каждого из них. Вдали от минимумов допускаются неустранимые разрывы первого рода. Для нахождения окрестности глобального минимума используется из 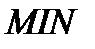метод случайного поиска (его комбинация). Методом сопряженных градиентов минимум уточняется. При появлении «оврагов» градиентные методы отказываются работать. В этом случае подключается к 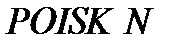овражный метод Гельфанда И.М., который позволяет осуществить многомерный поиск минимума, [Растригин Л.А.]. Из точки 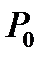по двум направлениям выполняется наискорейший спуск на «дно оврага», (рис.3.9а).

Рис.3.9а. Элемент многомерного поиска оптимума (по схеме ) :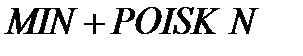

- где взять ближайшую точку – Эвристика! – ближайшая точка совпадает с .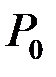

Но срабатывает помеха! Для этого, при вычислении градиента, вначале берем шаг 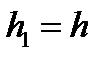, а потом шаг 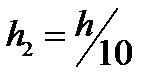, получаем точки 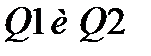, определяющие прямую линию – «дно оврага». По «дну оврага» выполняем еще один многомерный поиск минимума. Получим точку 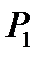. При необходимости этот элемент поиска можно повторить. Последовательность 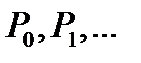задает убывающую последовательность целевой функции 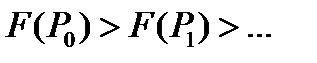. После срабатывания правила остановки, когда реализуется заданный порог похожести 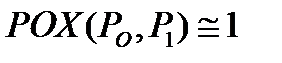, (рис. 3.9а. и ПП с именем SIM). Последняя полученная точка 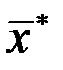и значение функции в этой точке будут точкой глобального минимума .

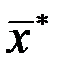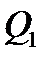Результаты анализа сравниваемых состояний представляются визуально. Порог похожести задается разработчиком -а. Точки и считаются лежащими на дне оврага (рис.3.9а). Эти две точки определяют прямую линию, по которой осуществляется одномерный поиск минимума. Одно из направлений в точке 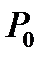является градиентным. Второе направление будет случайным. Эта комбинация, детерминированного и случайного поиска, приводит к желаемому результату. Регулирующими параметрами элемента поиска является пара ( 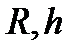), где 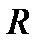- первоначальный шаг. В качестве правила остановки, при наискорейшем спуске на дно оврага и принятом механизме случайного выбора решения из полученного набора эвристик, используется принцип «похожести» точек [55]. Одной из эвристик алгоритма является предварительное знание об области 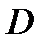и примерной зоне поиска 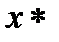, в которой находится минимум функции 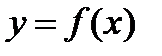, а также знание об изменении параметров технологического процесса по их «похожести» (значения должны быть одинаковыми, или близкими). Эта информация позволит оценить первоначальный шаг 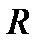и значения функции 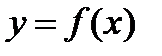в выбранных точках функциональных значений 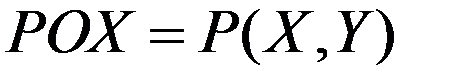на экране монитора (рис.5, табл. П.1).

Рис. 5. «Похожесть» диагностируемого состояния (при сравнении с нормативным значением 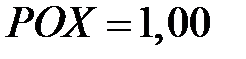) и определение фактического значения 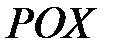(общее состояние энергоустановки) как расстояния между ними, определяемое по формуле [55]:

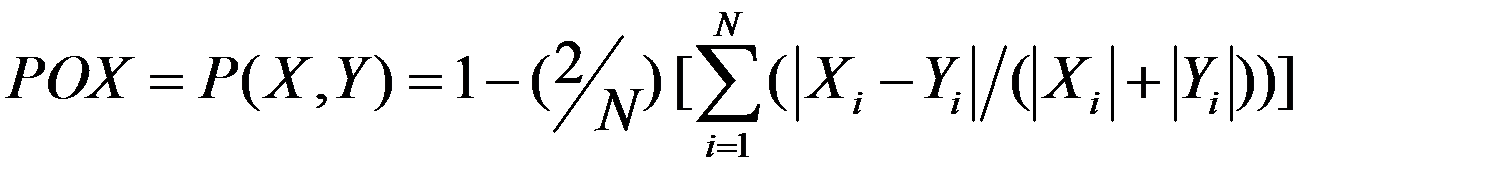,[55].

Здесь 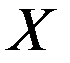- вектор измеренных параметров; 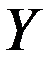- вектор эталонных значений параметров; 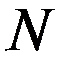- количество анализируемых параметров; 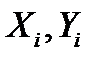- наборы значений признаков (параметров состояния) для диагностируемого ( 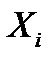) и эталонного ( 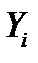) объектов (агрегатов), 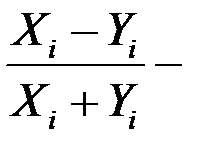коэффициент Фехнера (см. закон Вебера-Фехнера, 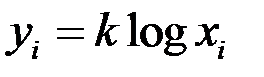, где 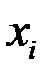- оценка некоторой величины 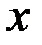при «ощущении» ).

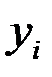При этом, 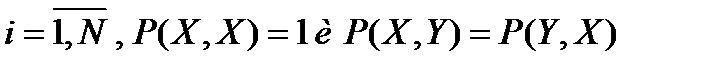. Если известно 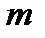элементов – эталонов 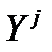, где 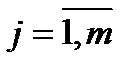, то, используя понятие «похожесть», можно найти ближайший к данному объекту 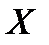(его состоянию) эталон 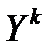по максимуму значения коэффициента 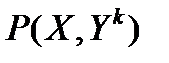, где .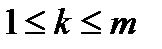

Таблица П.1

Массив «весов» параметров-признаков (отклонение мощности турбины ΔN_Э и ее экономичности Δ 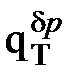от гарантийного значения, DELTA = ΔN_Э/Δ 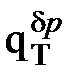) турбоустановки Т – 100 – 130 ТМЗ ст. №7 Н ТЭЦ – 4 (в отдельных опытах до и после ремонта) и сравнение параметров состояний по мере «похожесть» (РОХ). Режим работы – конденсационный.

Номинальные (гарантийные) параметры		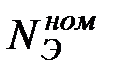		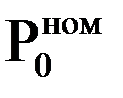		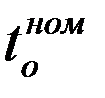		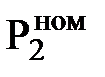	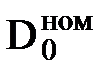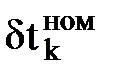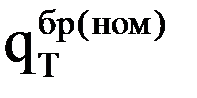РОХ	DELTA
МВт	МПа	0С	МПа	т/ч	0С	м3/ч	кДж/ кВт×ч	-	МВт/кДж/кВт×ч
110,0	12,8	555,0	0,0049	480,0	5,8			1,00	-
Фактические параметры	Перед ремонтом	79,73	12,29	552,4	0,0218	392,6	22,5			0,52
75,09	12,29	549,8	0,0216	366,6	14,2			0,65
64,5	12,87	546,0	0,019	326,6	12,6			0,61
55,84	12,94	547,7	0,0156	302,2	13,4			0,57
После ремонта	83,1	12,8		0,0121	330,8	24,7			0,66	0,52/10,05
85,7	12,9		0,0059	339,7	22,2			0,64	0,61/15,9
78,0	12,8		0,0052	323,6	22,2			0,67	0,39/14,2
71,1	13,04		0,0056	289,0	24,3			0,61	0,92/10,9
82,3	12,92		0,0061	332.7	17,1			0,66	0,63/15,9

Здесь под РОХ («похожесть», Рис.5) понимается расстояние между признаками

(точнее их совокупностью образов) состояний энергоустановки близких номинальному (нормативному) состоянию. Похожесть фактического состояния энергоустановки номинальному состоянию определяется по формуле, [55]:

.

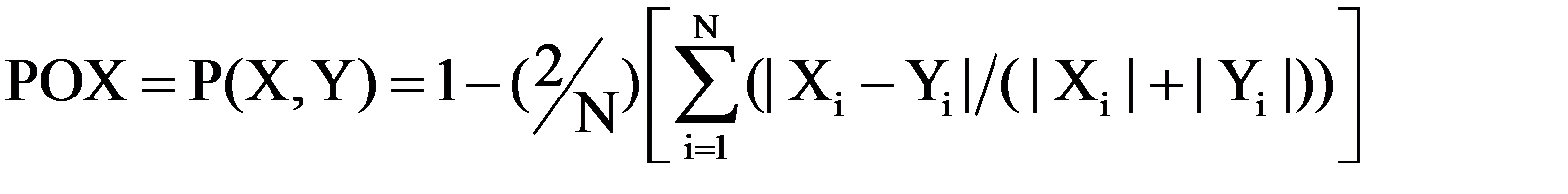Похожесть диагностируемых состояний определяется с помощью программы РОХ из . В геометрической интерпретации значения отображают (представляют) собой колебательную линию, построенную по параметрам оцениваемого состояния относительно его эталонного значения 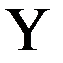, (рис.5).

Регулирование этими параметрами с использованием «меры похожести» 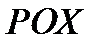позволяет эффективно (и визуально на экране монитора) применять диалоговый подход при оптимизации задач тепловой электростанции (ТЭС). В этом случае лицу принимающему решение (ЛПР) желательно иметь не одно, а группу хороших решений и возможности принятия решения по времени для последующего выбора окончательного оптимального решения (например, при базовом и переходном режимах работы энергоустановки). Для реализации этого в используемые эвристические правила вводится неопределенность исходной информации, благодаря чему и будет порождаться класс субоптимальных решений. Эвристические правила, обладающие ограниченной неопределенностью, назовем «размытыми» эвристиками [55]. Результатом поиска будет единственное решение, близость которого к оптимальному решению определяется величиной максимальной похожести , если мы имеем дело с тестовой задачей.

Тестовые задачи сконструированы авторами работы так, чтобы выделить особенности теплоэнергетического процесса. При опробовании а по схеме 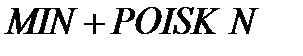на тестовых примерах (использованы функции Розенброка Х.Х. - 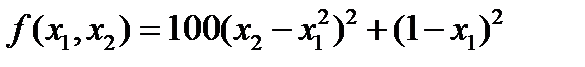и РастригинаЛ.А.- ) алгоритм сходится, т.е. минимум осуществляется из любой начальной точки. Использование механизма случайного выбора решений позволяет расширять область возможных реализаций или сужать ее, в зависимости от ситуации и готовности энергоустановки по состоянию к выполнению режима.

Задачи математического программирования при четкой постановке, в приложении к задачам технической диагностики энергоустановок ТЭС, решаем следующим образом.

Пусть в области 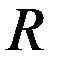, определяемой ограничениями

,

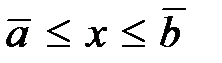(1)

задана целевая, в общем случае, нелинейная функция 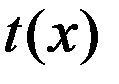. Требуется найти такой , для которого справедливо

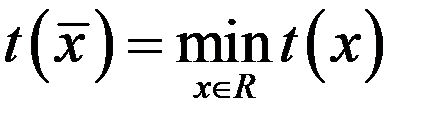. (2)

Здесь условие (1) означает, что каждая компонента вектора (матрицы) 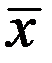изменяется в пределах от соответствующего наименьшего допустимого значения 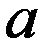до наибольшего допустимого значения 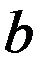. Количество компонент - 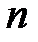. Любой вектор 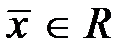называется допустимым. Вектор назовем оптимальным, если для любого другого вектора выполняется условие:

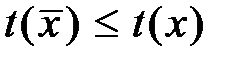. (3)

Как известно из теории исследования операций, [54], использование градиентных методов для решения многоэкстремальных задач затруднительно и малоэффективно, так как необходимы полные исследования целевой функции (определение, можно приближенное, вида поверхности, начальные приближения). Поэтому, как это подтверждает практика, наиболее результативными методами поиска минимума могут быть различные модификации случайного поиска. С этой целью в модуль включена модификация метода случайного поиска – метод “Монте-Карло”, [55].

Формула изменения координат вектора имеет следующий вид:

(4)

где - случайное число, ;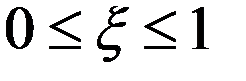

– нижние и верхние ограничения на переменные.

Из (4) следует, что точка 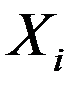при любом 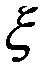всегда находится в области 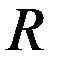(в ограничителях). Для определения случайного числа 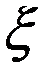используется процедура RAND, вырабатывающая случайные числа, необходимые при поиске окрестности глобального минимума функции цели. Попадание в окрестность глобального минимума происходит с некоторой вероятностью:

(5)

где 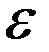- объем зоны критерия глобального минимума;

- объем зоны поиска;

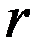– количество случайных бросков.

Работа метода прекращается, если количество случайных бросков превышает заданное целое число . Из совокупности точек, полученных в результате случайных бросков, выбирается точка 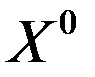, которая соответствует наименьшему значению функции цели 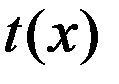. Однако метод Монте-Карло нецелесообразно использовать для нахождения , так как вероятность случайного попадания в - окрестность на одном шаге поиска, определяемая отношением объемов 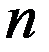– мерных гиперсфер с радиусами и (начальным расстоянием до цели), равна:

(6)

Среднее число шагов, необходимое для случайного попадания в 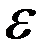- окрестность цели

(7)

имеет экспоненциальный характер и, следовательно, с ростом 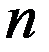быстро растет и . В схеме 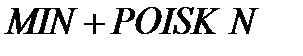этот метод используется для двух целей:

1) проведение статистических испытаний и расчетных экспериментов на ЭВМ;

2) оценки окрестности глобального экстремума функции цели.

В последнем случае точка 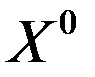, найденная методом “Монте–Карло”, улучшается постепенным приближением к цели путем ограничения поиска зоной, стягивающейся к наилучшей случайной пробе. Это значит, что случайные пробы производятся в объеме, центром которого является точка с наименьшим значением функции цели. По мере производства случайных испытаний этот объем стягивается к своему центру.

Если в процессе испытаний была найдена точка с меньшим значением функции цели, то объем испытаний устанавливается вокруг этой новой точки. Таким образом, зона испытаний перемещается в район цели, причем на каждом шаге вероятность случайного нахождения наилучшей точки становится все большей. Этот принцип лежит в основе второй модификации случайного поиска – методе случайного направленного поиска, [54, 55]. Из точки делается случайный шаг

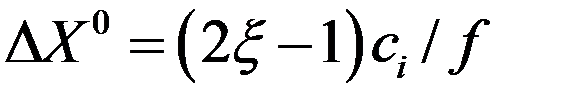, (8)

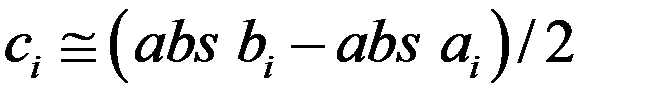где . (9)

Величина 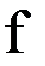на начальном шаге принимается равной . Затем определяется координата новой точки

, (10)

и сравниваются значения

. (11)

При этом 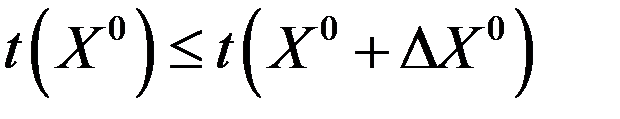считается неудачной ситуацией, а при 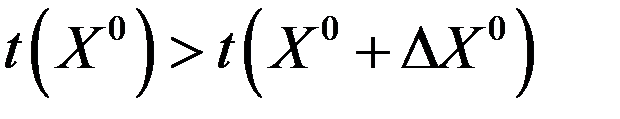проверяется условие

, (12)

при выполнении которого ситуацию также считают неудачной и удачной – в противном случае. При неудаче предусмотрен возврат в точку 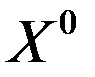, из которой делается шаг в диаметрально противоположном направлении с последующей проверкой условия (12). В случае неудачи вновь происходит возвращение в точку 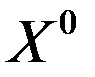, из которой делается столько случайных шагов, сколько потребуется для нахождения удачной ситуации. Если такая точка найдена, то через нее и 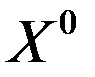проводится вектор, в направлении которого начинается движение с постоянным шагом.

При движении по выбранному направлению проверяется относительное изменение функции цели

. (13)

В случае предусмотрено возвращение в точку с последующим выбором (с помощью случайных испытаний) нового направления.

Значение 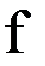меняется, в процессе минимизации, следующим образом.

Как только число неудачных шагов фиксированной точки окажется равным заданному целому числу , то 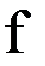увеличивается на единицу.

Эта операция позволяет осуществлять поиск и движение в выбранном направлении с все более и более уменьшающимися шагами.

Метод случайного направленного поиска прекращает свою работу, если выполняется условие (заданное целое число >>1). Если координаты точки вдруг оказываются вне ограничений, то функции присваивается число 10¹⁰ (или любое другое, определяемое на основе расчетных экспериментов).

Предполагая, что окрестность глобального минимума найдена, продолжается дальнейшее улучшение точки минимума. Для этого в схеме 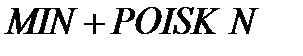используется метод сопряженных градиентов с преобразованием координат, [55], (рис.3.9а).

Задачи математического программирования в нечетких условиях,в приложении к задачам технической диагностики энергоустановок, решаются следующим образом, [123]:

«Под ситуацией принятия решений, при выборе диагноза состояния условимся понимать»:

- множество альтернатив, из которых лицо, принимающее решение (ЛПР), производит выбор;

- множество ограничений, накладываемых на этот выбор;

- целевую функцию, которая позволяет ЛПР ранжировать имеющиеся у него альтернативы.

В результате, каждое ЛПР, имея множество сформулированных целей, способно определить свои предпочтения.

Но на практике, особенно при диагностике в реальном масштабе времени, картина принятия решений резко меняется, так как ЛПР вынуждено применять следующее утверждение: '' должно быть в окрестности 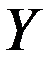''! А это уже подчеркивает появление нечеткости в формулировании цели, согласно [17, 123].

Выражение «в окрестности…», представим нечетким подмножеством 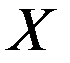, определяемым функцией (точнее, ее отображением ):

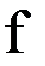, (14)

где 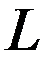- полная дистрибутивная решетка; 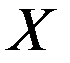– множество альтернатив.

В результате принятия решения по одному из предлагаемых диагнозов, представим возникшую нечеткую обстановку как множество 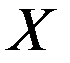– альтернатив вместе с его нечеткими подмножествами. Эти подмножества представляют собой также нечетко сформулированные критерии (цели и ограничения), т.е. систему:

. (15)

Здесь 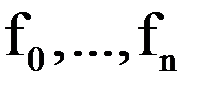– целевые функции.

Перебирая, по возможности, все критерии при выборе наиболее предположительного диагноза, можно построить функцию

. (16)

Оптимум, в этом случае, будет соответствовать той области 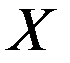, элементы которой максимизируют диагноз . В результате проведенных рассуждений можно определить нечеткую обстановку такой задачи тройкой . Предположим при этом, что решение задачи диагноза в нечеткой постановке будет определяться в виде нечеткого подмножества универсального множества альтернатив. Под оптимальным решением при этом будем понимать элемент 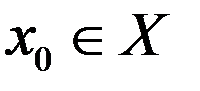(если такой существует), для которого, согласно [123]:

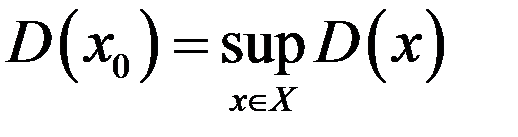, (17)

где - нечеткое решение; означает , означает . Таким образом, задача минимизации решений при выборе предположительного диагноза сведена к задаче нечеткого математического программирования (НМП), т.е. к задаче многокритериальной оптимизации.

Итак, под задачей НМП будем понимать задачу нахождения 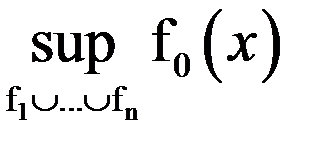, или

. (18)

Результат решения задачи минимизации функции цели

В данной работе было уделено внимание на реализацию комплексного решения оптимального нахождения минимума различных функций цели с помощью среды MathCAD 14. Рассмотрены и представлены ниже, при участии магистранта института прикладной информатики НГУЭУ А.Е. Некипелова, в комплексе метод «Монте-Карло» и градиентный метод наискорейшего спуска, позволяющие уточнить минимум функции, начальное приближение которого получается из случайного поиска методом Монте-Карло.

1. Метод «Монте-Карло»

Для минимизации функции многих переменных разработано множество численных методов, но большинство из них связано с подсчётом градиента функции, что со своей стороны может дать эффективные алгоритмы вычисления лишь, если удаётся аналитически подсчитать частные производные. Между тем, более универсальным методом минимизации функции многих переменных является метод перебора, при котором произвольным образом разбивается область определения функций на симплексы и в каждом узле симплекса вычисляется значение функции цели, причём происходит сравнение – перебор значений и на печать выводится точка минимума и значение функции в этой точке.

В методе «Монте-Карло» зададим функцию . Выбираем область поиска решения задачи:

;

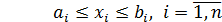а) Производим случайные броски, т.е. выбираем значения 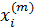для каждой переменной по формуле:

;

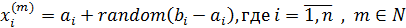б) Сравниваем значения функции:

,

если это неравенство выполняется, то

,

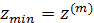если не выполняется, то

;

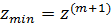в) Количество случайных бросков либо фиксировано, либо уточняется при достижении необходимой определенной погрешности.

Метод градиентного спуска

Строгий аналитический метод не всегда приводит к цели (случай, когда в критической точке). В подобных, и в более сложных случаях применяют различные приближённые аналитические методы, которые в математическом смысле иногда менее строго обоснованы, но, тем не менее, порой приводят к желаемому результату. К таким методам относятся и градиентные методы наискорейшего спуска.

Пусть, нам нужно найти . Рассмотрим некоторую точку

и вычислим в этой точке градиент функции :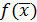

,

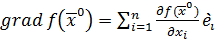где 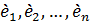- ортонормированный базис в пространстве .

Если 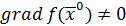, то полагаем:

,

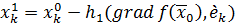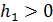где , а выбирается из условия сходимости итерационного процесса:

,

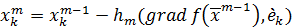где , а выбирается из условия сходимости.

Формулу можно расписать в виде:

…………………………………………………………………

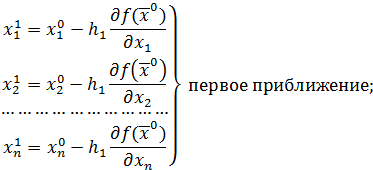
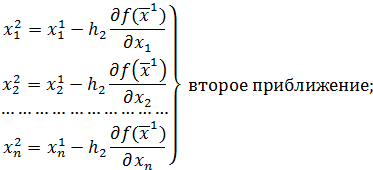
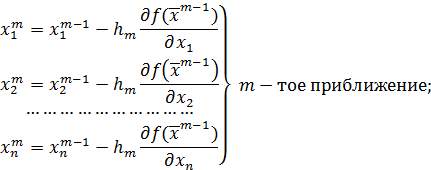
Здесь m – число итераций. Процесс итерации останавливается, когда достигается требуемая предельная погрешность, т.е. когда выполнены условия остановки итерации:

.

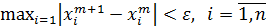Данный метод хорош лишь в том случае, когда имеется некое первое оптимальное приближение, в противном случае результат может быть совсем иной, не удовлетворяющий критериям. Поэтому в данной работе мы используем его в комплексе с методом «Монте-Карло», в дальнейшем, получив начальное приближение, уточним его до некоторой погрешности градиентным методом наискорейшего спуска.

ПРИМЕР РЕАЛИЗАЦИИ И РЕШЕНИЯ ЗАДАЧИ определЕНИЯ МИНИМУМА ФУНКЦИИ ЦЕЛИ В СРЕДЕ MATHCAD

Пусть задана многоэкстремальная функция:

.

Рассмотрим ее графики при различных изменениях . Из первого графика видим, что глобальный экстремум находится в районах 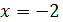и равен примерно 75.

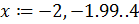
Если смотреть другую область изменения, то глобальный экстремум находится в районе . Рассмотрим область изменения .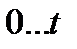

Используем метод «Монте-Карло» для нахождения глобального минимума функции. Сформируем два вектора 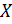и , присвоив их нулевым элементам значение нуль:

Зададим количеством случайных чисел 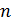, которое мы будем использовать для вычисления минимума. Чем больше это количество, тем точнее будет результат вычисления:

.

С помощью функции 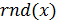создадим вектор случайных значений элементов . Функция генерирует равномерно распределенные случайные числа в интервале 0… .

Из графика видно, что нам достаточен интервал .

.

Теперь в векторе 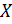помещено 100000 случайных чисел. Вычислим значения функции от них и поместим их в вектор .

.

Величину минимального элемента этого вектора найдем, используя функцию .

Величину минимального элемента вектора 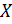найдем, используя небольшую программу и вычислим по ней ответ:

,

,

.

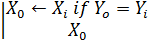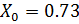Получили первое приближенное значение минимума функции цели. Для уточнения значения используем градиентный метод. Поиск минимума ведется по следующим формулам:

,

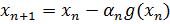выбирается из условия .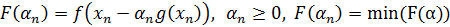

– параметр, определяющий погрешность поиска минимума.

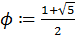- отношение золотого сечения.

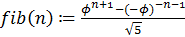- формула Бине

для вычисления чисел Фибоначчи, где 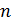– номер числа.

Сделаем подпрограмму для вычисления частной производной функции в точке заданной вектором по переменной .

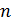Подпрограмма выглядит следующим образом:

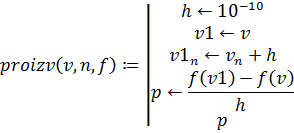
Сделаем подпрограмму для вычисления значений проекций градиента на оси координат. Подпрограмма возвращает вектор значений проекций и использует подпрограмму вычисления частной производной:

.

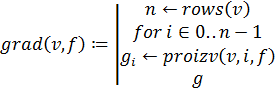Функция , используемая для выбора :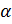

.

Далее сделаем подпрограмму поиска минимума функции одной переменной по методу Фибоначчи (одномерной оптимизации функции цели).

Подпрограмма поиска минимума с помощью метода градиентного спуска:

Сформулируем еще раз нашу многоэкстремальную функцию: