Лекция 3. Числовые множества

Основные понятия:

счетные множества; несчетные множества; числовые множества; ограниченным сверху (снизу) множества; верхняя (нижняя) грань множества; граничная точка множества; граница множества; комбинаторика; соединения; размещения; перестановки; сочетания; множество комплексных чисел; комплексное число; действительная часть комплексного числа; мнимая часть комплексного числа; число 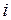; сложение комплексных чисел; умножение комплексных чисел; тригонометрическая форма комплексных чисел; абсолютная величина комплексного числа; аргумент комплексного числа; комплексно сопряженное число; формула Муавра.

Основные понятия

Будем рассматривать множества, элементами которых являются числа. Такие множества называются числовыми. Числовые множества задаются на оси действительных чисел R. На этой оси выбирают масштаб и указывают начало отсчета и направление. Наиболее распространенные числовые множества:

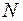· ‑ множество натуральных чисел;

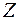· ‑ множество целых чисел;

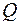· – множество рациональных или дробных чисел;

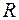· ‑ множество действительных чисел.

Множество всех рациональных чисел является счетным множеством. Счетным является множество всех точек плоскости (пространства) имеющих рациональные координаты.

Множество всех действительных чисел является несчетным: оно имеет мощность, называемую континуумом.

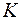Некоторое непустое подмножество множества действительных чисел называют ограниченным сверху (снизу), если существует действительное число такое, что 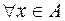выполняется неравенство ( ).

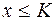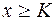Всякое число 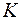с указанным свойством называют верхней (нижней) гранью множества .

Непустое подмножество множества действительных чисел называется ограниченным, если оно ограничено и сверху и снизу.

В противоположность этому определению, множество называется неограниченным сверху (снизу), если какое бы число 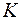мы бы не предложили в качестве верхней (нижней) границы множества , всегда найдется элемент этого множества, который будет больше (меньше) .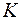

Множество, неограниченное как сверху, так и снизу, называется неограниченным множеством.

Наименьшую из верхних граней непустого подмножества множества действительных чисел называют точной верхней гранью этого множества и обозначают sup . Наибольшую из нижних граней непустого подмножества множества действительных чисел называют точной нижней гранью этого множества и обозначают inf . Символы sup и inf являются сокращениями от supremum (самый верхний) и infimum (самый нижний).

Примем без доказательства утверждение о том, что всякое ограниченное сверху (снизу) множество имеет точную верхнюю (нижнюю) грань.

Граничной точкой множества называется точка, у которой в любом содержащем ее открытом промежутке найдутся как точки, принадлежащие множеству, так и точки, не принадлежащие множеству. Сама граничная точка может, как принадлежать множеству, так и не принадлежать ему.

Граница множества – совокупность граничных точек множества:

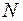· (множество натуральных чисел) ограниченно снизу (например, числом 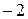) и не ограничено сверху;

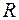· (множество действительных чисел) неограничено;

· множество отрицательных чисел неограничено снизу и ограничено сверху.

Соединения. Бином Ньютона

Рассмотрим совокупность различных элементов 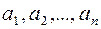. Произвольная упорядоченная выборка из этих элементов:

( ; )

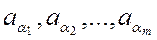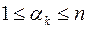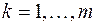называется соединением. Эта выборка может быть как без повторений, так и с повторениями.

Раздел элементарной математики, в котором для конечных множеств рассматриваются различные соединения элементов, такие, как сочетания, размещения, перестановки, а также все виды соединений с повторениями называется комбинаторика. Задачи комбинаторики впервые рассматривались в связи с возникновением теории вероятностей, где к задачам комбинаторики приводит подсчет вероятностей на основе гипотезы равновозможных элементарных событий.

Размещениями 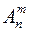из элементов по 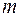( 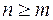) называют их соединения, каждое из которых содержит ровно 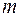различных элементов (выбранных из данных элементов) и которые отличаются либо сами элементами, либо порядком элементов.

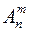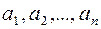Определим число размещений из элементов по .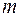

Будем строить произвольное соединение 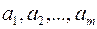последовательно. Сначала определим его первый элемент 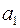. Очевидно, что из данной совокупности элементов его можно выбрать различными способами. После выбора первого элемента 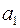, для второго элемента 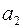остается 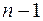способов выбора и т.д. Так как каждый такой выбор дает новое размещение, то все эти выборы можно свободно комбинировать между собой. Для 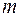элементов формула приобретает вид:

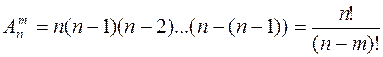
Соединения из элементов, каждое из которых содержит все элементов, и которые отличаются лишь порядком элементов, называются перестановками .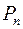

Перестановки являются частным случаем размещений. Так как каждая перестановка содержит все элементов множества, то различные перестановки отличаются друг от друга только порядком элементов.

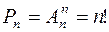
Сочетаниями 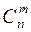из элементов по 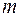( 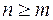) называют такие их соединения, каждое из которых содержит ровно 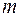данных элементов, и которые отличаются хотя бы одним элементом.

Рассмотрим все допустимые сочетания элементов .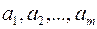

Делая в каждом из них 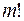возможных перестановок их элементов, очевидно, получим все размещения из элементов по :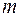

.

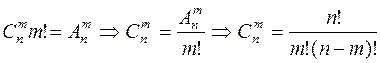Числа 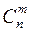являются коэффициентами в формуле бинома Ньютона:

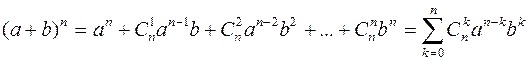
Свойства сочетаний:

1.

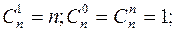
2.

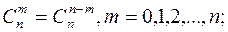
3.

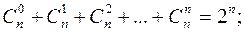
4.

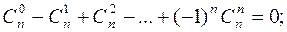
5.

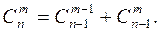
Свойства 1 и 2 очевидно следуют из определения 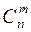, свойства 3 и 4 доказываются с помощью бинома Ньютона, полагая для свойства 3 что 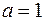и 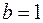, а для свойства 4 что 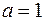и 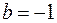. Свойство 5 можно проверить следующим образом:

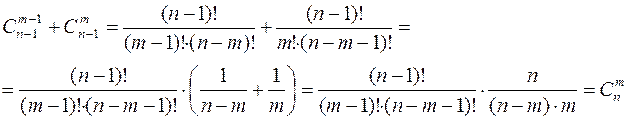
Это свойство позволяет последовательно вычислять биномиальные коэффициенты 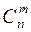с помощью так называемого треугольника Паскаля:

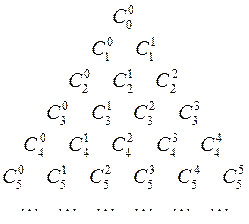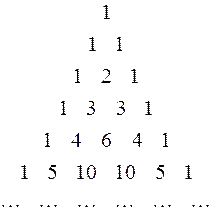Здесь каждое число, кроме крайних единиц, является суммой двух вышерасположенных.

Комплексные числа

В арифметике и алгебре рассматривают различные действия над числами: арифметические (сложение, вычитание, умножение, деление), возведение в степень, извлечение корня и т.д. Только два действия – сложение и умножение – безусловно, выполнимы в области натуральных чисел: сумма и произведение натуральных чисел - также натуральные числа. Однако в области арифметики натуральных чисел уже вычитание не всегда выполнимо – для возможности образования разности двух натуральных чисел множество 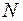нужно дополнить до множества целых чисел 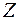, введя в него ноль и целые отрицательные числа. Такие операции как деление и извлечение корня становятся выполнимыми только после расширения рассматриваемой числовой области: множество целых чисел должно быть, соответственно, дополнено вначале до множества 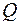за счет введения рациональных чисел, а потом и до множества действительных чисел 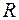за счет введения иррациональных чисел.

Этот процесс можно схематически изобразить цепочкой 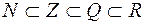, где 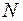, , 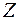, 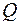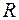обозначают соответственно множества натуральных, целых, рациональных и действительных чисел. Причем каждая последующая числовая система сохраняет все основные свойства предыдущей и обладает рядом новых полезных свойств. Так, в 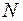можно только складывать и умножать, в 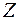можно уже вычитать, в 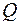‑ делить. Во множестве 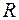действительных чисел можно извлекать корни любой степени из положительных чисел, хотя в 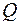даже число 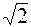не имеет смысла. Но и в множестве действительных чисел 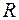такое простое уравнение 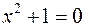не имеет решений. Так как многие задачи практики приводят к алгебраическим уравнениям, требуется построить новое множество, содержащее множество действительных чисел и решение любого алгебраического уравнения. Символом 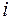, который называется мнимой единицей, обозначим корень уравнения 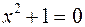, или 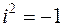. Множество 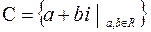, которое представляет собой множество всех двучленов вида 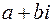, называется множеством комплексных чисел. Действительное число 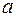называется действительной частью комплексного числа 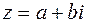, 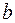‑ мнимой частью или коэффициентом при мнимой единице. Два комплексных числа 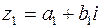и 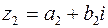будут равны тогда и только тогда, когда 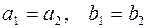. При этом действительные числа рассматриваются как частный случай комплексных чисел, мнимая часть которых равна нулю ( 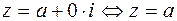). Комплексное число равно нулю тогда и только тогда, когда равны нулю его действительная и мнимая части.

Операции сложения, вычитания и умножения над числами вида 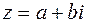производятся по обычным правилам алгебры с единственным дополнительным условием: