Математическая модель воздействия угроз на информационную систему обработки персональных данных
Шувалов И.А. 1 Семенчин Е.А. 2
1 Управление ГИБДД ГУ МВД России по Краснодарскому краю
2 ФГБОУ ВПО «Кубанский государственный университет»
В работе предложена математическая модель воздействия внутренних и внешних угроз на информационную систему обработки персональных данных «Информационные ресурсы Управления ГИБДД», используемую в служебной деятельности сотрудниками Управления государственной инспекцией безопасности дорожного движения Главного управления Министерства внутренних дел России по Краснодарскому краю. Поэтапно описан процесс построения двух математических моделей информационной системы: а) с помощью марковской цепи с непрерывным временем; б) с помощью марковской цепи с дискретными моментами перехода из одного состояния в другое. Предложена методика выявления актуальных угроз безопасности персональных данных при их обработке в рассматриваемой информационной системе. Приведены примеры расчетов вероятностей нахождения математической модели информационной системы в одном из трех рассматриваемых состояний (угроза не наступила, угроза наступила, но не была реализована, и угроза реализована).
В статьях [10, 11] предложена имитационная модель функционирования сегментов информационной системы «Информационные ресурсы Управления ГИБДД», используемой в повседневной деятельности сотрудниками УГИБДД ГУ МВД по Краснодарскому краю и подчиненными ему подразделениями. С помощью этой модели можно определить (выявить) угрозы, которые представляют реальную опасность для информационной системы. Однако, используя статистические данные, можно определить такие угрозы также методами математического моделирования.
Цель данной работы – предложить математическую модель воздействия угроз на указанную информационную систему и на основе этой модели разработать методику их выявления.
Рассматриваемую информационную систему можно интерпретировать как систему массового обслуживания, в которую поступают угрозы (заявки). Вначале рассмотрим ситуацию, когда на вход системы поступают угрозы одного типа, предполагая при этом, что данная угроза не может быть реализована или наступить несколько раз в один и тот же момент времени. Если выполнены указанные предположения, то система может находиться в трёх различных состояниях (рис. 1):
1) угроза не поступала, а значит, не была реализована;
2) угроза поступала, но не была реализована;
3) угроза поступала и была реализована.

Рис. 1. Ориентированный граф
Модель системы, которая может находиться в указанных состояниях, предложена в работах А.П. Росенко [7, 9]. В данных работах допускалось наличие поглощающих состояний системы и выполнение требования: система не может находиться в одном состоянии в течении некоторого отрезка времени. Указанные допущения не позволяют использовать предложенную в [7, 9] математическую модель для анализа информационной системы «Информационные ресурсы УГИБДД», потому что, как показал анализ многолетних наблюдений, у системы поглощающие состояния отсутствуют: реализация угрозы либо никак не влияет на работоспособность системы в целом, либо может вывести из строя на непродолжительный промежуток времени один из её сегментов. Если же учитывать возможность возврата системы в исходное состояние, то можно будет изучить её поведение на протяжении длительного промежутка времени.
Математическая модель информационной системы «Информационные ресурсы УГИБДД»
Рассматриваемая система является системой с восстановлением, так как состояние x2 не является поглощающим, а значит, система может вернуться из x2 в исходное состояние. Будем рассматривать систему с непрерывным временем. Переход из состояния в состояние в системе осуществляется согласно ориентированному графу, представленному на рис. 1. Для описания процесса перехода из состояния в состояние построим матрицу интенсивностей перехода [1]
 (1)
(1)
Из предыдущих соглашений следует, что элементы этой матрицы должны удовлетворять условиям:
λ12 = –λ11;
λ22 = –λ21 – λ23; (2)
λ33 = –λ31 – λ32.
Требования (2) необходимы для выполнения условий, предъявляемых к элементам матрицы интенсивностей [1]:
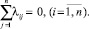
Элементы матрицы интенсивностей переходов могут быть найдены (вычислены) с помощью имитационной модели, предложенной в [11]. В данной работе опишем вероятностно-аналитический способ их определения. Согласно [1], в соответствии с видом информационной системы (см. рис. 1), для определения вероятностей p0(t), p1(t), p2(t) имеем систему дифференциальных уравнений
 (3)
(3)
с начальными условиями
p0(0) = 1; p1(0) = 0; p2(0) = 0. (4)
Задачу Коши (3), (4), представляющую собой математическую модель рассматриваемой информационной системы, можно решить численно, если воспользоваться известными пакетами прикладных программ (например, пакетом «Mathcad», разработанным фирмой Parametric Technology Corporation).
Если моменты времени перехода t являются дискретными, то есть переход системы из состояния в состояние осуществляется в строго определенный момент времени, матрица вероятностей перехода из состояния в состояние за один шаг имеет вид (1), матрица вероятностей перехода за n шагов (в момент t = n) – следующий вид [3, 9]:
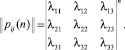 (5)
(5)
Так как p(0) = (1, 0, 0) (см. 4) задан, то вектор абсолютных вероятностей p(n) = (p0(n), p1(n), (p2(n)) определяется соотношением
 (6)
(6)
Примеры численной реализации непрерывной и дискретной моделей
Пример 1. Пусть матрица интенсивностей перехода (1) имеет вид:
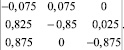
Построим решение задачи (3), (4) методом Рунге–Кутты четвертого порядка для момента времени t = 50 с количеством шагов 4 на каждую единицу времени (рис. 2), воспользовавшись пакетом прикладных программ «MathCad».
В результате проведенных вычислений найдены значения вероятностей p0(t), p1(t), p2(t) для различных моментов времени, которые представлены в табл. 1
Таблица 1
Результаты вычислений значений p0(t), p1(t), p2(t) для различных моментов времени
| Значение времени t | Вероятность нахождения системы в состоянии x0 | Вероятность нахождения системы в состоянии x1 | Вероятность нахождения системы в состоянии x2 |
| 0,951 | 0,049 | ||
| 0,93 | 0,069 | 0,001 | |
| 0,922 | 0,076 | 0,002 | |
| 0,919 | 0,079 | 0,002 | |
| 0,918 | 0,08 | 0,002 | |
| 0,917 | 0,081 | 0,002 | |
| … | … | … | … |
| 0,917 | 0,081 | 0,002 | |
| … | … | … | … |
| 0,917 | 0,081 | 0,002 |
Следовательно, в момент времени t = 50 p0(t) = 0,917, p1(t) = 0,081, p2(t) = 0,002.
В соответствии с данными, приведенными в табл. 1, построим график изменения значений вероятностей нахождения системы в одном из состояний в зависимости от времени t (рис. 2).

Рис. 2. График изменения значений вероятностей pi(t), i = 0, 1, 2 в зависимости от времени t
Пример 2. Пусть моменты перехода t системы из состояния в состояние являются дискретными (t = n, n = 1, …, 8), а матрица вероятностей перехода за один шаг имеет вид:

начальное распределение:
p(0) = (1,0,0).
Вычислим вероятности нахождения системы в каждом из состояний xi, i = 0, 1, 2, через 8 шагов, воспользовавшись пакетом прикладных программ «MathCad». Результаты вычислений представлены в табл. 2.
Таблица 2
Результаты вычислений, полученные с использованием программного обеспечения «MathCad»
| Шаг эксперимента | Вероятность нахождения системы в состоянии x0 | Вероятность нахождения системы в состоянии x1 | Вероятность нахождения системы в состоянии x2 |
| 0,9 | 0,1 | ||
| 0,88 | 0,1 | 0,02 | |
| 0,864 | 0,108 | 0,028 | |
| 0,856 | 0,111 | 0,033 | |
| 0,852 | 0,113 | 0,035 | |
| 0,849 | 0,114 | 0,037 | |
| 0,848 | 0,115 | 0,038 | |
| 0,847 | 0,115 | 0,038 |
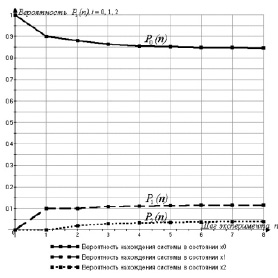
Рис. 3. График изменения значений вероятностей pi(t), i = 0, 1, 2 в зависимости от шага эксперимента n
По данным табл. 2 построен график изменения значений вероятностей p0(t), p1(t), p2(t) (рис. 3):
Заключение
В работе предложена математическая модель реализации угроз безопасности информационной системы «Информационные ресурсы УГИБДД», а также методика выявления актуальных угроз безопасности исследуемой системы, разработанная на основе этой модели.
Примеры численных результатов анализа модели с помощью предложенной методики показывают, что их использование позволяет выделить угрозы, которые являются актуальными для рассматриваемой информационной системы и могут использоваться на практике. Недостатком предложенной методики является необходимость рассмотрения поведения модели системы при воздействии на неё отдельно каждого типа угроз и невозможность изучения поведения при воздействии нескольких угроз одновременно. Вместе с тем, изучение поведения модели при воздействии на неё каждой угрозы в отдельности позволяет более детально изучить каждый тип угрозы и выделить те, вероятность наступления которых является наиболее высокой.
Рецензенты:
Лебедев К.А., д.ф.-м.н., профессор кафедры прикладной математики, ФГБОУ ВПО «Кубанский государственный университет», г. Краснодар;
Приходько А.И., д.т.н., профессор кафедры общего, стратегического, информационного менеджмента и бизнес-процессов, ФГБОУ ВПО «Кубанский государственный университет», г. Краснодар.
Работа поступила в редакцию 15.08.2013.
Библиографическая ссылка
Шувалов И.А., Семенчин Е.А. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ВОЗДЕЙСТВИЯ УГРОЗ НА ИНФОРМАЦИОННУЮ СИСТЕМУ ОБРАБОТКИ ПЕРСОНАЛЬНЫХ ДАННЫХ // Фундаментальные исследования. – 2013. – № 10-3. – С. 529-533;
URL: https://fundamental-research.ru/ru/article/view?id=32312 (дата обращения: 12.09.2017).
1. Алиев Т.И. Основы моделирования дискретных систем: учебное пособие. – СПб: СПбГУ ИТМО, 2009. – 363 с.
2. Вентцель Е.С. Теория вероятностей. – М.: Наука, 1969. – 576 с.
3. Волков И.К., Зуев С.М., Цветкова Г.М. Случайные процессы: учебник для вузов / под ред. В.С. Зарубина, А.П. Крищенко. – М.: МГТУ им.Баумана, 1999. – 448 с.
4. Зыков С.В. Введение в теорию программирования. Функциональный подход. – Учебный Центр безопасности информационных технологий Microsoft МИФИ, 2003.
5. Калиткин Н.Н. Численные методы. – М.: Наука, 1978. – 512 с.
6. Кирьянов Д.В. Самоучитель Mathcad 11. – СПб.: БХВ-Петербург, 2003. – 560 с.: ил.
7. Росенко А.П. Математическое моделирование влияния внутренних угроз на безопасность конфиденциальной информации, циркулирующей в автоматизированной информационной системе Известия ЮФУ. Технические науки. Тематический выпуск. «Информационная безопасность». – Таганрог: Изд-во ТТИ ЮФУ, 2008. – № 8 (85).
8. Солодов А.П., Очков В.Ф. Mathcad/Дифференциальные модели. – М.: Издательство МЭИ, 2002. – 239 с.: ил.
9. Теоретические основы анализа и оценки влияния внутренних угроз на безопасность конфиденциальной информации: монография / А.П. Росенко. – М.: Гелиос АРВ, 2008. – 154 с.
10. Шувалов И.А., Росенко А.П. Имитационная модель реализации внутренних и внешних угроз безопасности информационной системы на сегменте «коммутатор – сервер» // Вестник Дагестанского государственного университета. – 2013. – Вып. 1. – С. 112–123.
11. Шувалов И.А., Семенчин Е.А. Имитационная модель реализации внутренних и внешних угроз безопасности информационной системы на сегменте «Маршрутизатор – маршрутизатор» // Фундаментальные исследования. – 2012. – № 9. – С. 425–431.
В статьях [10, 11] предложена имитационная модель функционирования сегментов информационной системы «Информационные ресурсы Управления ГИБДД», используемой в повседневной деятельности сотрудниками УГИБДД ГУ МВД по Краснодарскому краю и подчиненными ему подразделениями. С помощью этой модели можно определить (выявить) угрозы, которые представляют реальную опасность для информационной системы. Однако, используя статистические данные, можно определить такие угрозы также методами математического моделирования.
Цель данной работы – предложить математическую модель воздействия угроз на указанную информационную систему и на основе этой модели разработать методику их выявления.
Рассматриваемую информационную систему можно интерпретировать как систему массового обслуживания, в которую поступают угрозы (заявки). Вначале рассмотрим ситуацию, когда на вход системы поступают угрозы одного типа, предполагая при этом, что данная угроза не может быть реализована или наступить несколько раз в один и тот же момент времени. Если выполнены указанные предположения, то система может находиться в трёх различных состояниях (рис. 1):
1) угроза не поступала, а значит, не была реализована;
2) угроза поступала, но не была реализована;
3) угроза поступала и была реализована.

Рис. 1. Ориентированный граф
Модель системы, которая может находиться в указанных состояниях, предложена в работах А.П. Росенко [7, 9]. В данных работах допускалось наличие поглощающих состояний системы и выполнение требования: система не может находиться в одном состоянии в течении некоторого отрезка времени. Указанные допущения не позволяют использовать предложенную в [7, 9] математическую модель для анализа информационной системы «Информационные ресурсы УГИБДД», потому что, как показал анализ многолетних наблюдений, у системы поглощающие состояния отсутствуют: реализация угрозы либо никак не влияет на работоспособность системы в целом, либо может вывести из строя на непродолжительный промежуток времени один из её сегментов. Если же учитывать возможность возврата системы в исходное состояние, то можно будет изучить её поведение на протяжении длительного промежутка времени.
Математическая модель информационной системы «Информационные ресурсы УГИБДД»
Рассматриваемая система является системой с восстановлением, так как состояние x2 не является поглощающим, а значит, система может вернуться из x2 в исходное состояние. Будем рассматривать систему с непрерывным временем. Переход из состояния в состояние в системе осуществляется согласно ориентированному графу, представленному на рис. 1. Для описания процесса перехода из состояния в состояние построим матрицу интенсивностей перехода [1]
 (1)
(1)
Из предыдущих соглашений следует, что элементы этой матрицы должны удовлетворять условиям:
λ12 = –λ11;
λ22 = –λ21 – λ23; (2)
λ33 = –λ31 – λ32.
Требования (2) необходимы для выполнения условий, предъявляемых к элементам матрицы интенсивностей [1]:
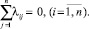
Элементы матрицы интенсивностей переходов могут быть найдены (вычислены) с помощью имитационной модели, предложенной в [11]. В данной работе опишем вероятностно-аналитический способ их определения. Согласно [1], в соответствии с видом информационной системы (см. рис. 1), для определения вероятностей p0(t), p1(t), p2(t) имеем систему дифференциальных уравнений
 (3)
(3)
с начальными условиями
p0(0) = 1; p1(0) = 0; p2(0) = 0. (4)
Задачу Коши (3), (4), представляющую собой математическую модель рассматриваемой информационной системы, можно решить численно, если воспользоваться известными пакетами прикладных программ (например, пакетом «Mathcad», разработанным фирмой Parametric Technology Corporation).
Если моменты времени перехода t являются дискретными, то есть переход системы из состояния в состояние осуществляется в строго определенный момент времени, матрица вероятностей перехода из состояния в состояние за один шаг имеет вид (1), матрица вероятностей перехода за n шагов (в момент t = n) – следующий вид [3, 9]:
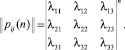 (5)
(5)
Так как p(0) = (1, 0, 0) (см. 4) задан, то вектор абсолютных вероятностей p(n) = (p0(n), p1(n), (p2(n)) определяется соотношением
 (6)
(6)
Примеры численной реализации непрерывной и дискретной моделей
Пример 1. Пусть матрица интенсивностей перехода (1) имеет вид:
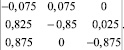
Построим решение задачи (3), (4) методом Рунге–Кутты четвертого порядка для момента времени t = 50 с количеством шагов 4 на каждую единицу времени (рис. 2), воспользовавшись пакетом прикладных программ «MathCad».
В результате проведенных вычислений найдены значения вероятностей p0(t), p1(t), p2(t) для различных моментов времени, которые представлены в табл. 1
Таблица 1
Результаты вычислений значений p0(t), p1(t), p2(t) для различных моментов времени
| Значение времени t | Вероятность нахождения системы в состоянии x0 | Вероятность нахождения системы в состоянии x1 | Вероятность нахождения системы в состоянии x2 |
| 0,951 | 0,049 | ||
| 0,93 | 0,069 | 0,001 | |
| 0,922 | 0,076 | 0,002 | |
| 0,919 | 0,079 | 0,002 | |
| 0,918 | 0,08 | 0,002 | |
| 0,917 | 0,081 | 0,002 | |
| … | … | … | … |
| 0,917 | 0,081 | 0,002 | |
| … | … | … | … |
| 0,917 | 0,081 | 0,002 |
Следовательно, в момент времени t = 50 p0(t) = 0,917, p1(t) = 0,081, p2(t) = 0,002.
В соответствии с данными, приведенными в табл. 1, построим график изменения значений вероятностей нахождения системы в одном из состояний в зависимости от времени t (рис. 2).

Рис. 2. График изменения значений вероятностей pi(t), i = 0, 1, 2 в зависимости от времени t
Пример 2. Пусть моменты перехода t системы из состояния в состояние являются дискретными (t = n, n = 1, …, 8), а матрица вероятностей перехода за один шаг имеет вид:

начальное распределение:
p(0) = (1,0,0).
Вычислим вероятности нахождения системы в каждом из состояний xi, i = 0, 1, 2, через 8 шагов, воспользовавшись пакетом прикладных программ «MathCad». Результаты вычислений представлены в табл. 2.
Таблица 2
Результаты вычислений, полученные с использованием программного обеспечения «MathCad»
| Шаг эксперимента | Вероятность нахождения системы в состоянии x0 | Вероятность нахождения системы в состоянии x1 | Вероятность нахождения системы в состоянии x2 |
| 0,9 | 0,1 | ||
| 0,88 | 0,1 | 0,02 | |
| 0,864 | 0,108 | 0,028 | |
| 0,856 | 0,111 | 0,033 | |
| 0,852 | 0,113 | 0,035 | |
| 0,849 | 0,114 | 0,037 | |
| 0,848 | 0,115 | 0,038 | |
| 0,847 | 0,115 | 0,038 |

Рис. 3. График изменения значений вероятностей pi(t), i = 0, 1, 2 в зависимости от шага эксперимента n
По данным табл. 2 построен график изменения значений вероятностей p0(t), p1(t), p2(t) (рис. 3):
Заключение
В работе предложена математическая модель реализации угроз безопасности информационной системы «Информационные ресурсы УГИБДД», а также методика выявления актуальных угроз безопасности исследуемой системы, разработанная на основе этой модели.
Примеры численных результатов анализа модели с помощью предложенной методики показывают, что их использование позволяет выделить угрозы, которые являются актуальными для рассматриваемой информационной системы и могут использоваться на практике. Недостатком предложенной методики является необходимость рассмотрения поведения модели системы при воздействии на неё отдельно каждого типа угроз и невозможность изучения поведения при воздействии нескольких угроз одновременно. Вместе с тем, изучение поведения модели при воздействии на неё каждой угрозы в отдельности позволяет более детально изучить каждый тип угрозы и выделить те, вероятность наступления которых является наиболее высокой.
Рецензенты:
Лебедев К.А., д.ф.-м.н., профессор кафедры прикладной математики, ФГБОУ ВПО «Кубанский государственный университет», г. Краснодар;
Приходько А.И., д.т.н., профессор кафедры общего, стратегического, информационного менеджмента и бизнес-процессов, ФГБОУ ВПО «Кубанский государственный университет», г. Краснодар.
Работа поступила в редакцию 15.08.2013.
Библиографическая ссылка
Шувалов И.А., Семенчин Е.А. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ВОЗДЕЙСТВИЯ УГРОЗ НА ИНФОРМАЦИОННУЮ СИСТЕМУ ОБРАБОТКИ ПЕРСОНАЛЬНЫХ ДАННЫХ // Фундаментальные исследования. – 2013. – № 10-3. – С. 529-533;
URL: https://fundamental-research.ru/ru/article/view?id=32312 (дата обращения: 12.09.2017).
