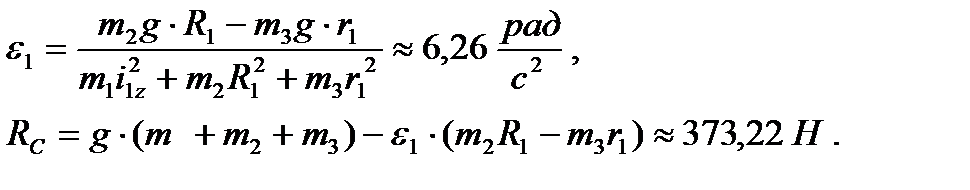Приведение к центру даламберовых сил инерции точек твердого тела

Если принцип Даламбера применить для изучения движения твердого тела, то силы инерции, приложенные к каждой точке тела, образуют непрерывную нагрузку, распределенную по объему тела. В соответствии с основной теоремой статики эту нагрузку можно эквивалентным образом заменить одной силой и одной парой сил, приведя ее к выбранному центру приведения. В данном случае в качестве центра приведения удобно выбирать центр масс тела. При этом главный вектор сил инерции не зависит от выбора центра приведения и вычисляется по формуле

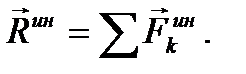
Для главного момента сил инерции относительно центра масс будем иметь

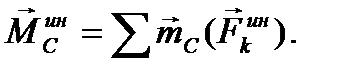
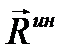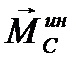Получим далее выражения для и в общем случае при произвольном движении тела. Запишем формулы, выражающие теорему о движении центра масс и теорему об изменении кинетического момента относительно центра масс для рассматриваемого тела

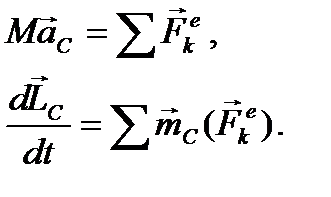(85)

Если сопоставить уравнения (85) с формулами, выражающими принцип Даламбера для тела

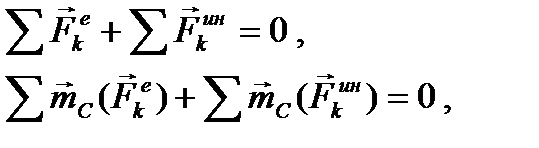
то получим

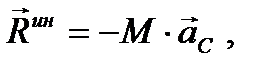(86)

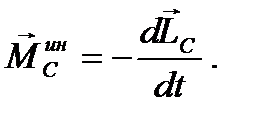(87)

Формулы (86), (87) выражают главный вектор сил инерции тела через массу тела и ускорение его центра масс и главный момент сил инерции через кинетический момент тела. Эти формулы справедливы при любом движении тела. Отметим, что в общем случае вычисление главного момента сил инерции по формуле (87) является довольно сложной задачей.

Рассмотрим несколько частных случаев.

1. Поступательное движение тела. Можно доказать, что в этом случае 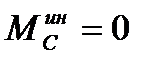и все силы инерции, приложенные к точкам тела, можно заменить равнодействующей силой, вычисляемой по формуле (86) и приложенной в центре масс тела (см. рис. 54)

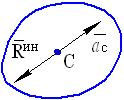
Рис. 54

2. Вращательное и плоское движение тела. При этих видах движения тела главный момент сил инерции относительно центра масс вычисляется по достаточно простой формуле

(88)

только в случае, когда ось Сz является главной осью инерции тела в точке С и центробежные моменты инерции, содержащие индекс этой оси, равны нулю. Это условие, например, выполняется в случаях, когда ось Сz является осью материальной симметрии тела или плоскость xCy является плоскостью материальной симметрии. При этом в случае вращательного движения тела под осью Cz понимается ось, проведенная через центр масс параллельно оси вращения, а при плоском движении тела ось Сz следует провести через центр масс перпендикулярно плоскости движения.

3. Построение эпюры сил инерции. Рассмотрим случай, когда твердое тело является однородным стержнем и силы инерции точек тела представляют собой непрерывно распределенную нагрузку из параллельных сил, для которой легко построить эпюру. В этом случае силы инерции точек тела можно заменить равнодействующей силой, равной главному вектору сил инерции и вычисляемой по формуле (86). Точка ее приложения может быть найдена по соответствующей формуле из раздела статика.

Поясним этот случай примером.

Пример 14

К вертикальному валу АВ длиной 1 м, закрепленному с помощью подпятника А и цилиндрического шарнира В, в его средней точке Dпод углом 30º к вертикали жестко прикреплен стержень DE длиной 0,6 м и массой 20 кг (см. рис. 55). Вся конструкция вращается вокруг вертикальной оси с постоянной угловой скоростью ω=10 рад/c.

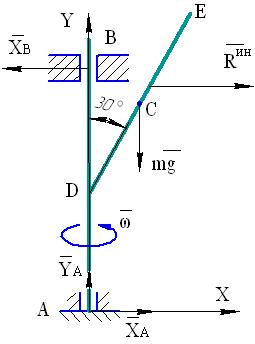
Рис. 55

Определить реакции в опорах А и В. Массой вала АВ пренебречь.

Решение

Применим принцип Даламбера ко всей конструкции. Обозначим на рис. 55 силу тяжести 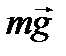, приложенную в центре масс стержня DE.

Далее построим эпюру сил инерции точек стержня DE. При постоянной угловой скорости ускорение 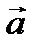произвольно выбранной частицы стержня массой dm будет направлено к оси вращения и по величине равно 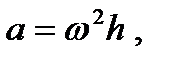где 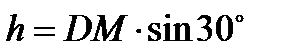- расстояние от частицы до оси вращения. Соответствующая сила инерции частицы 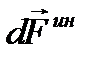будет направлена противоположно вектору 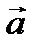(см. рис. 56). Величина этой

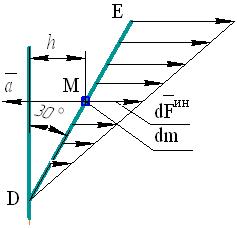
Рис. 56

силы инерции вычисляется по формуле

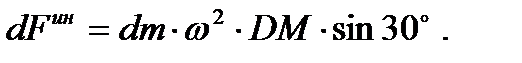
Она пропорциональна расстоянию частицы от конца D стержня, принимая наименьшее значение, равное нулю, в точке D и наибольшее значение в точке Е. Следовательно, в данном случае силы инерции точек стержня образуют непрерывно распределенную нагрузку с треугольной эпюрой (см. рис. 56). Такую нагрузку можно заменить равнодействующей силой, равной главному вектору сил инерции

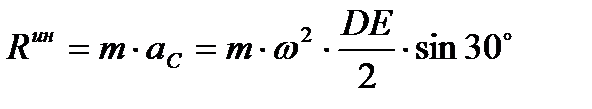
и приложенной на расстоянии 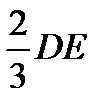от точки D. Покажем эту равнодействующую силу на рис. 55.

В ответ на действие сил 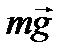и 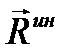, расположенных в плоскости рисунка, в опорах А и В возникнут реакции 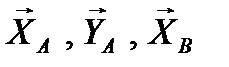, лежащие в той же плоскости. Обозначим эти реакции опор на рис. 55.

Таким образом, в соответствии с принципом Даламбера получили уравновешенную плоскую произвольную систему сил. Запишем для нее три независимых уравнения равновесия:

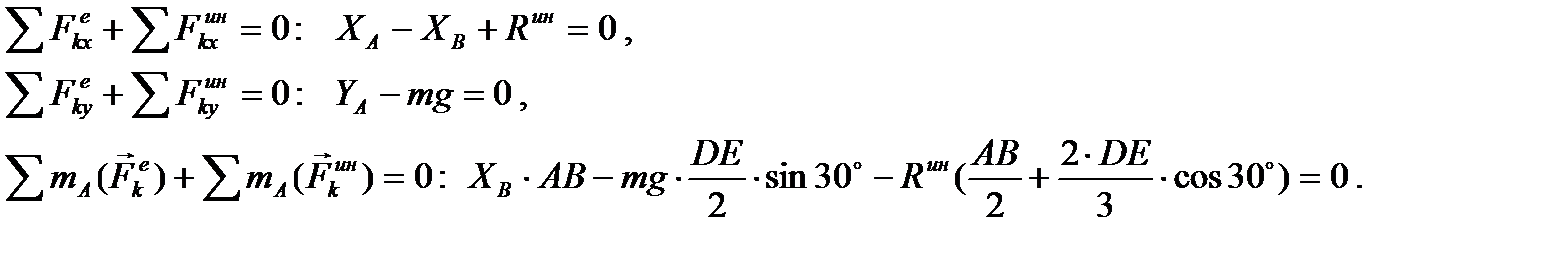
Подставляя сюда численные значения величин и решая систему уравнений, найдем 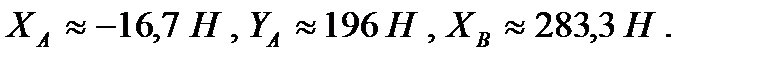Результаты расчетов показывают, что истинное направление реакции 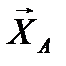противоположно указанному на рис. 55.

Рассмотрим решение еще одной задачи.

Пример 15

Механизм, состоящий из ступенчатого шкива 1, а также подвешенных к нему грузов 2 и 3 ( см. рис. 57 ), приходит в движение из состояния

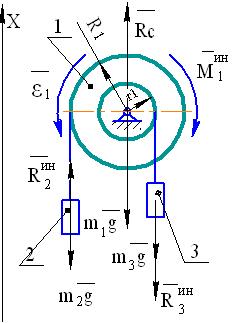
Рис. 57

покоя под действием сил тяжести. Заданы массы тел 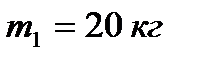, , 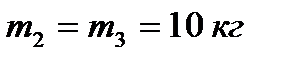радиусы 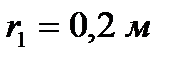, 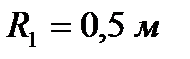и радиус инерции шкива относительно оси вращения .

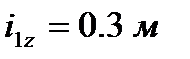Найти угловое ускорение шкива и реакцию опорного шарнира С. Трением в шарнире пренебречь.

Решение

Применим принцип Даламбера для всего механизма. Обозначим на рис. 57 внешние силы, действующие на тела механизма: силы тяжести 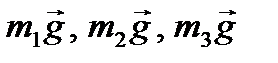и реакцию опорного шарнира 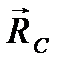. Дополним эту систему сил силами инерции. Для тел 2 и 3, движущихся поступательно, равнодействующие сил инерци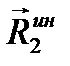и и 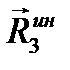будут направлены противоположно ускорениям тел. Их величины равны

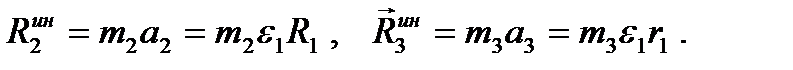
Силы инерции точек шкива 1 приведем к центру масс С. Получим главный вектор сил инерции

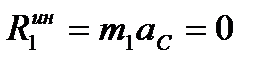
и главный момент сил инерции

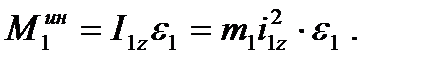
Соответствующая пара сил инерции направлена противоположно угловому ускорению 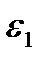(см. рис. 57).

Для полученной плоской параллельной системы сил составим два независимых уравнения равновесия:

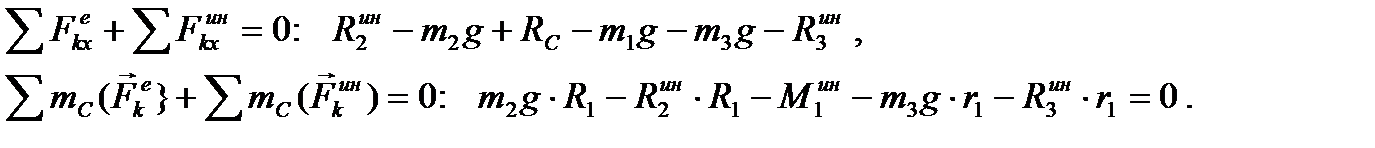
Подставляя в эти уравнения значения сил инерции, получим

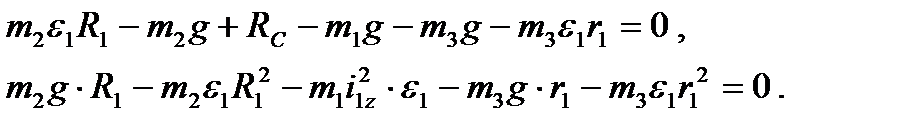
Решая полученную систему уравнений, найдем