Частные случаи динамической теоремы Кориолиса

Принцип относительности классической механики

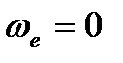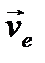Пусть переносное движение подвижной системы координат является поступательным, прямолинейным и равномерным. В этом случае и является постоянным вектором. Тогда

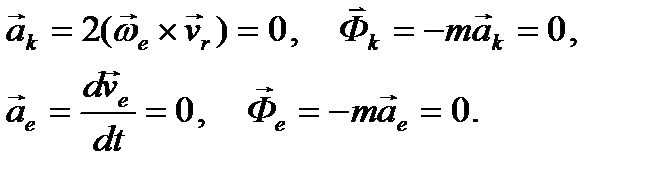
В результате для такой подвижной системы координат основное уравнение динамики относительного движения примет вид

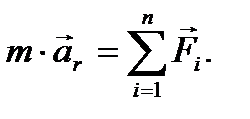
То есть, относительное движение в такой системе координат происходит только под действием обычных сил, как и в неподвижной системе координат, независимо от направления и скорости движения подвижной системы координат.

Всякая система координат, движущаяся относительно основной системы поступательно, прямолинейно и равномерно, называется инерциальной.

Наблюдатель, находящийся в инерциальной системе координат в замкнутом помещении, с помощью любых физических опытов не может определить, находится ли его система в покое или движется в какую-либо сторону по инерции.

В этом заключается впервые сформулированный Галилеем принцип относительности классической механики: законы динамики одинаковы во всех инерциальных системах координат.

Случай относительного покоя

Рассмотрим частный случай, когда точка находится в равновесии относительно подвижной системы координат. В этом случае относительная скорость 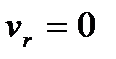. Тогда 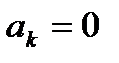и сила инерции Кориолиса равна нулю. Кроме того, при относительном покое относительное ускорение 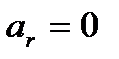. В результате уравнение (12) примет вид

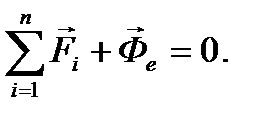(16)

Уравнение (16) выражает условие относительного покоя, которое формулируется в виде: для равновесия материальной точки относительно подвижной системы координат необходимо и достаточно, чтобы приложенные к точке силы уравновешивались с переносной силой инерции.

Эффекты от действия сил инерции, возникающих за счет

Вращения Земли

Рассмотрим далее некоторые эффекты, обусловленные действием переносной и кориолисовой сил инерции при движении тел по земной поверхности. Будем учитывать только вращение Земли вокруг собственной оси, проходящей через северный и южный полюсы (см. рис. 5).

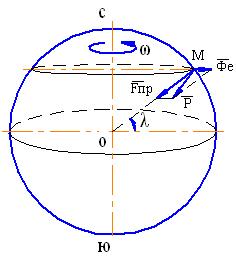
Рис. 5

Изучим вначале действие переносной силы инерции. Земля вращается вокруг своей оси с постоянной угловой скоростью, поэтому на материальную точку, находящуюся у земной поверхности, действует переносная сила инерции, направленная от оси вращения (см. рис. 5). Величина этой силы инерции пропорциональна расстоянию от точки до оси вращения. Она обращается в нуль на полюсе и достигает максимального значения на экваторе.

В связи с этим сила тяжести 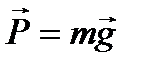, получающаяся как результат геометрического сложения силы притяжения со стороны Земли 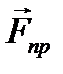и переносной силы инерции (см. рис. 5), будет изменяться в зависимости от географической широты λ. Соответственно будет изменяться и ускорение свободного падения g , принимая максимальное значение на полюсе и минимальное – на экваторе.

Если рассмотреть находящийся в равновесии грузик, подвешенный на нити, то линия отвеса (продолжение нити) будет отклоняться от перпендикуляра к земной поверхности, проходящего через центр Земли, если точка подвеса не находится на полюсе или экваторе (см. рис. 6).

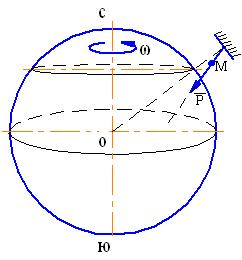
Рис. 6

Рассмотрим теперь действие кориолисовой силы инерции. Пусть точка движется со скоростью 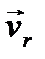по поверхности Земли вдоль меридиана в северном полушарии (см. рис. 7). При этом ускорение Кориолиса

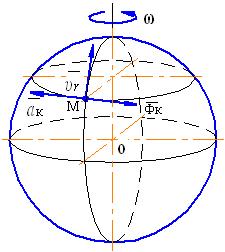
Рис. 7

будет направлена влево по отношению к направлению движения, а сила инерции Кориолиса – вправо. Можно доказать, что при движении точки по поверхности Земли в северном полушарии в любом направлении кориолисова сила инерции будет направлена вправо по отношению к направлению движения.

Действием кориолисовой силы инерции объясняется ряд наблюдаемых на практике явлений, такие как отклонение артиллерийского снаряда вправо от линии прицеливания и более быстрое изнашивание правого рельса железнодорожных путей. Этим же можно объяснить эмпирически установленный закон Бэра, в соответствии с которым правый берег рек, протекающих в северном полушарии, обычно является более крутым. Аналогичным образом можно доказать, что за счет действия кориолисовой силы инерции падающие на Землю в северном полушарии тела отклоняются к востоку от вертикали.