Рассмотрим гамильтонов цикл как последовательность ребер. Напомним, что окрестностью 2-замена называют множество всех гамильтоновых циклов, получающихся из заданного заменой двух несмежных ребер. Такая окрестность содержит 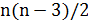 элементов, что несколько меньше, чем в окрестности city-swap.
элементов, что несколько меньше, чем в окрестности city-swap.
На рис. 5.18 показано различие между этими окрестностями. Для окрестности 2-замена удаление ребер 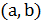 и
и 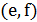 приводит к появлению двух новых ребер
приводит к появлению двух новых ребер 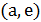 и
и 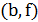 и обратному обходу дуг от
и обратному обходу дуг от 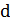 до
до  . Если в окрестности city-swap в перестановке поменять местами
. Если в окрестности city-swap в перестановке поменять местами 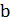 и
и 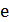 , то появятся четыре новых ребра
, то появятся четыре новых ребра 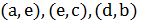 и
и 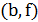 , но обход дуг от
, но обход дуг от 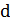 до
до  останется прежним.
останется прежним.
L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEAEHn9jcYA AADbAAAADwAAAGRycy9kb3ducmV2LnhtbESPT2vCQBTE7wW/w/KE3urGHkpNXUVsCz30n9pCvT2z zySYfRt2nzH99q5Q6HGYmd8w03nvGtVRiLVnA+NRBoq48Lbm0sDX5vnmHlQUZIuNZzLwSxHms8HV FHPrT7yibi2lShCOORqoRNpc61hU5DCOfEucvL0PDiXJUGob8JTgrtG3WXanHdacFipsaVlRcVgf nYHmJ4bXXSbb7rF8k88Pffx+Gr8bcz3sFw+ghHr5D/+1X6yByQQuX9IP0LMzAAAA//8DAFBLAQIt ABQABgAIAAAAIQDw94q7/QAAAOIBAAATAAAAAAAAAAAAAAAAAAAAAABbQ29udGVudF9UeXBlc10u eG1sUEsBAi0AFAAGAAgAAAAhADHdX2HSAAAAjwEAAAsAAAAAAAAAAAAAAAAALgEAAF9yZWxzLy5y ZWxzUEsBAi0AFAAGAAgAAAAhADMvBZ5BAAAAOQAAABAAAAAAAAAAAAAAAAAAKQIAAGRycy9zaGFw ZXhtbC54bWxQSwECLQAUAAYACAAAACEAEHn9jcYAAADbAAAADwAAAAAAAAAAAAAAAACYAgAAZHJz L2Rvd25yZXYueG1sUEsFBgAAAAAEAAQA9QAAAIsDAAAAAA== " filled="f" stroked="f" strokeweight=".5pt">
Рисунок-5.18. Различия между окрестностями
Если вершины расположены на плоскости, а веса ребер вычисляются как евклидовы расстояния, то пересечение ребер 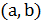 и
и 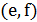 свидетельствует о возможности улучшения данного тура в силу неравенства треугольника. Однако это условие не является необходимым, и улучшение возможно даже без пересечения ребер.
свидетельствует о возможности улучшения данного тура в силу неравенства треугольника. Однако это условие не является необходимым, и улучшение возможно даже без пересечения ребер.
На основе окрестности 2-замена Лином и Керниганом предложена оригинальная эвристика. Она позволяет заменять произвольное число ребер и переходить от одного тура к другому, используя принципы жадных алгоритмов. Основная идея эвристики заключается в следующем. Удалим из гамильтонова цикла произвольное ребро, например 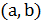 . В полученном пути один конец (вершину
. В полученном пути один конец (вершину 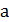 ) будем считать фиксированным, а другой конец будем менять, перестраивая гамильтонов путь. Добавим ребро из вершины
) будем считать фиксированным, а другой конец будем менять, перестраивая гамильтонов путь. Добавим ребро из вершины 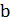 , например
, например 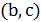 , и разорвем образовавшийся единственный цикл так, чтобы снова получить гамильтонов путь. Для этого придется удалить ребро, инцидентное вершине
, и разорвем образовавшийся единственный цикл так, чтобы снова получить гамильтонов путь. Для этого придется удалить ребро, инцидентное вершине  . Обозначим его
. Обозначим его 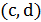 . Новый гамильтонов путь имеет концевые вершины
. Новый гамильтонов путь имеет концевые вершины 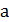 и
и 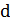 (рис. 5.19). Эту процедуру будем называть ротацией. Для получения нового гамильтонова цикла достаточно добавить ребро
(рис. 5.19). Эту процедуру будем называть ротацией. Для получения нового гамильтонова цикла достаточно добавить ребро 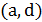 . Согласно алгоритму Лина – Кернигана, переход от одного тура к другому состоит из удаления некоторого ребра, выполнения серии последовательных ротаций и, наконец, замыкания концевых вершин полученного гамильтонова пути. Существуют различные варианты этой основной схемы, которые отличаются правилами выбора ротаций и ограничениями на множества удаляемых и добавляемых ребер. В алгоритме Лина – Кернигана ротации выбираются так, чтобы минимизировать разность
. Согласно алгоритму Лина – Кернигана, переход от одного тура к другому состоит из удаления некоторого ребра, выполнения серии последовательных ротаций и, наконец, замыкания концевых вершин полученного гамильтонова пути. Существуют различные варианты этой основной схемы, которые отличаются правилами выбора ротаций и ограничениями на множества удаляемых и добавляемых ребер. В алгоритме Лина – Кернигана ротации выбираются так, чтобы минимизировать разность 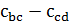 . При этом множества удаляемых и добавляемых ребер в серии ротаций не должны пересекаться. Последнее ограничение гарантирует, что число ротаций не превысит
. При этом множества удаляемых и добавляемых ребер в серии ротаций не должны пересекаться. Последнее ограничение гарантирует, что число ротаций не превысит 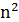 и трудоемкость одного шага (перехода от одного цикла к другому) останется полиномиальной. Общее число шагов алгоритма, по-видимому, не может быть ограничено полиномом, и известен вариант окрестности Лина – Кернигана, для которого задача коммивояжера становится
и трудоемкость одного шага (перехода от одного цикла к другому) останется полиномиальной. Общее число шагов алгоритма, по-видимому, не может быть ограничено полиномом, и известен вариант окрестности Лина – Кернигана, для которого задача коммивояжера становится
PLS-полной [23].
Рисунок-5.19. Процедура ротации
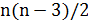 элементов, что несколько меньше, чем в окрестности city-swap.
элементов, что несколько меньше, чем в окрестности city-swap.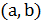 и
и 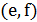 приводит к появлению двух новых ребер
приводит к появлению двух новых ребер 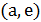 и
и 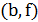 и обратному обходу дуг от
и обратному обходу дуг от 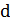 до
до  . Если в окрестности city-swap в перестановке поменять местами
. Если в окрестности city-swap в перестановке поменять местами 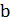 и
и 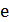 , то появятся четыре новых ребра
, то появятся четыре новых ребра 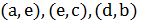 и
и 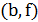 , но обход дуг от
, но обход дуг от 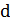 до
до  останется прежним.
останется прежним.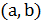 и
и 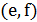 свидетельствует о возможности улучшения данного тура в силу неравенства треугольника. Однако это условие не является необходимым, и улучшение возможно даже без пересечения ребер.
свидетельствует о возможности улучшения данного тура в силу неравенства треугольника. Однако это условие не является необходимым, и улучшение возможно даже без пересечения ребер.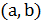 . В полученном пути один конец (вершину
. В полученном пути один конец (вершину 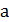 ) будем считать фиксированным, а другой конец будем менять, перестраивая гамильтонов путь. Добавим ребро из вершины
) будем считать фиксированным, а другой конец будем менять, перестраивая гамильтонов путь. Добавим ребро из вершины 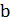 , например
, например 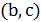 , и разорвем образовавшийся единственный цикл так, чтобы снова получить гамильтонов путь. Для этого придется удалить ребро, инцидентное вершине
, и разорвем образовавшийся единственный цикл так, чтобы снова получить гамильтонов путь. Для этого придется удалить ребро, инцидентное вершине  . Обозначим его
. Обозначим его 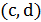 . Новый гамильтонов путь имеет концевые вершины
. Новый гамильтонов путь имеет концевые вершины 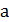 и
и 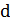 (рис. 5.19). Эту процедуру будем называть ротацией. Для получения нового гамильтонова цикла достаточно добавить ребро
(рис. 5.19). Эту процедуру будем называть ротацией. Для получения нового гамильтонова цикла достаточно добавить ребро 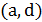 . Согласно алгоритму Лина – Кернигана, переход от одного тура к другому состоит из удаления некоторого ребра, выполнения серии последовательных ротаций и, наконец, замыкания концевых вершин полученного гамильтонова пути. Существуют различные варианты этой основной схемы, которые отличаются правилами выбора ротаций и ограничениями на множества удаляемых и добавляемых ребер. В алгоритме Лина – Кернигана ротации выбираются так, чтобы минимизировать разность
. Согласно алгоритму Лина – Кернигана, переход от одного тура к другому состоит из удаления некоторого ребра, выполнения серии последовательных ротаций и, наконец, замыкания концевых вершин полученного гамильтонова пути. Существуют различные варианты этой основной схемы, которые отличаются правилами выбора ротаций и ограничениями на множества удаляемых и добавляемых ребер. В алгоритме Лина – Кернигана ротации выбираются так, чтобы минимизировать разность 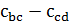 . При этом множества удаляемых и добавляемых ребер в серии ротаций не должны пересекаться. Последнее ограничение гарантирует, что число ротаций не превысит
. При этом множества удаляемых и добавляемых ребер в серии ротаций не должны пересекаться. Последнее ограничение гарантирует, что число ротаций не превысит 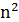 и трудоемкость одного шага (перехода от одного цикла к другому) останется полиномиальной. Общее число шагов алгоритма, по-видимому, не может быть ограничено полиномом, и известен вариант окрестности Лина – Кернигана, для которого задача коммивояжера становится
и трудоемкость одного шага (перехода от одного цикла к другому) останется полиномиальной. Общее число шагов алгоритма, по-видимому, не может быть ограничено полиномом, и известен вариант окрестности Лина – Кернигана, для которого задача коммивояжера становится 