Транспортная задача линейного программирования

Транспортная задача линейного программирования имеет следующую формулировку.

Имеется некоторый однородный продукт, сосредоточенный у m поставщиков A_i в количестве a_i (i=1, 2, …,m) единиц соответственно, необходимо доставить n потребителям B_j в количестве b_j(j=1, 2, …,n) единиц. Известна стоимость C_ij перевозки единицы груза от i–го поставщика к j–му потребителю. Необходимо составить план перевозок, позволяющий вывезти все грузы, полностью удовлетворить потребности и имеющий минимальную стоимость.

Математическую модель этой задачи можно представить в следующем виде.

Найти наименьшее значение линейной функции

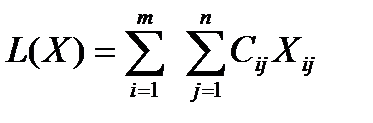
при ограничениях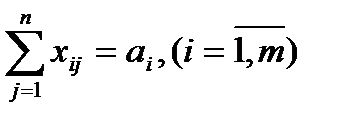

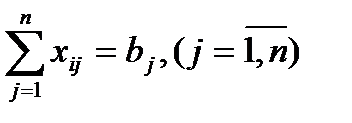
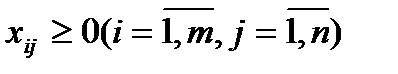
Обозначим через x_ij количество единиц груза, запланированных к перевозке от i-го поставщика к j-му потребителю; тогда условие задачи можно записать в виде таблицы 1.5, которую в дальнейшем будем называть матрицей планирования.

Таблица 1.5.

Поставщики	Потребители	Запасы
B1	B2	…	Bn
А1	C11 X11	C12 X12	….	C1n X1n	a1
А2	C21 X21	C22 X22	…	C2n X2n	a2
---	---	---	---	---	---
Аm	Cm1 Xm1	Cm2 Xm2	…	Cmn Xmn	am
Потребности	b1	b2	…	bn	=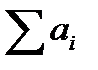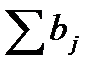

Составим математическую модель задачи. Т.к. от i-го поставщика к j-му потребителю запланировано к перевозке x_ij единиц груза, то стоимость перевозки составит C_ijX_ij. Стоимость всего плана выразим двойной суммой:

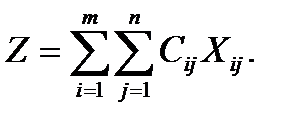
Сумму ограничений получаем из следующих условий задачи:

а) все грузы должны быть вывезены, т.е. 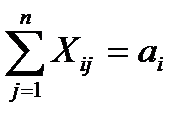(из строк таблицы);

б) все потребности должны быть удовлетворены, т.е. 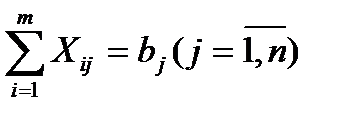(уравнения получаются из столбцов таблицы 6);

Таким образом, математическая модель транспортной задачи имеет следующий вид.

Найти наименьшее значение линейной функции

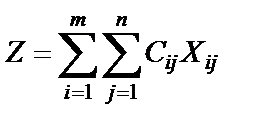(1.34)

при ограничениях

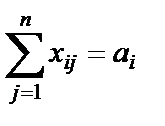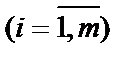	(1.35)
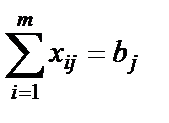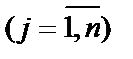	(1.36)
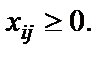	(1.37)

В рассмотренной модели предполагается, что суммарные запасы равны суммарным потребностям, т.е. 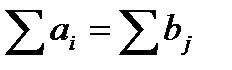. Такая модель называется закрытой.

Теорема. Любая транспортная задача, у которой суммарный объем запасов совпадает с суммарным объемом потребностей, имеет решение.

Алгоритм метода потенциалов.

1. Проверяем условие разрешимости транспортной задачи, т.е.

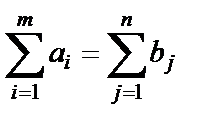(1.38)

Если это условие не выполняется, возможны два случая:

а) 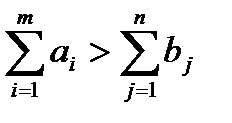,вводим фиктивного потребителя В_Ф =В_n+1, с потребностями b_Ф= .

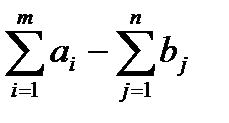б) 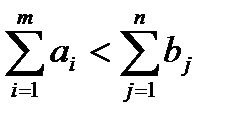, вводим фиктивного поставщика А_Ф =А_m+1, c ресурсами а_ф= _.

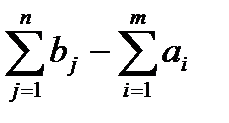В распределительную таблицу в первом случае вводится дополнительный столбец, а во втором случае дополнительная строка. Обычно стоимость фиктивных потребителей и поставщиков берется равной нулю.

2. Строим первоначальный опорный план. Существует ряд методов для его построения: метод «северо-западного угла», метод «наилучший элемент матрицы», метод «наилучший элемент строки», «аппроксимация» и др.

Рассмотрим метод наилучшего элемента матрицы:

a) среди всех стоимостей 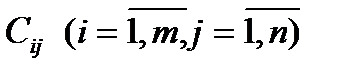выбираем наилучший элемент (если задача была поставлена на минимум, тогда выбирается наименьший, а если задача была поставлена на максимум, тогда наибольший элемент);

б) в клетку распределительной таблицы с наилучшим элементом записываем максимально возможную перевозку (поставку) с учетом ограничений по троке и столбцу. При этом ограничение по строке или столбцу исчерпывается, тогда соответствующий ряд в направлении исчерпанного ограничения в дальнейшем решений не рассматривается (т.е. вычеркивается);

в) переходим к шагу а). Процесс продолжается до тех пор, пока все ресурсы не будут распределены и весь спрос не будет удовлетворен.

Замечание 1:если при распределении поставок, одновременно вычеркивается строка и столбец, то получим вырожденный план.

Поэтому в одну из свободных клеток (не относящихся к фиктивным), с наилучшим C_ij в одновременно вычеркиваемых строке и столбце ставим нуль поставку, т.е. увеличиваем число занятых клеток до (m+n-1).

3. Проверяем условие невырожденности плана: количество заполненных клеток должно быть равно m+n-1. Если план вырожденный – устраняем вырождение (замечания 1 и 2).

4. Подсчитываем значение линейной формы L(Х).

5. Проверяем условие оптимальности плана:

a) для всех занятых клеток (т.е. X_ij>0 ) строим систему уравнений с (m+n) неизвестными U_i(i=1,m и V_j(j=1,n).

-U_i+V_j=C_ij.

Так как эта система является неопределенной, то можно одной переменной задать произвольное значение. Для простоты расчета полагаем вычисления предположим U₁=0. Полученные U_i и V_j вводим в дополнительные столбец и строку;

б) для всех свободных клеток (т.е. X_ij=0) производим оценку по формуле

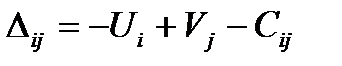
Если все 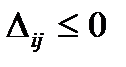при решении задачи на минимум (все 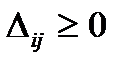при решении задачи на максимум), тогда полученный план будет оптимальным.

Выписываем план перевозок X=(X_ij) и значение L(X).

Если имеется хотя бы одна оценка 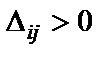при решении задачи на минимум ( 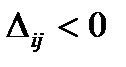при решении задачи на максимум), то план не оптимальный, и переходим к следующему шагу.

6. Среди всех положительных оценок (задача на минимум) выбираем наибольшую. При решении задачи на максимум, из всех отрицательных оценок 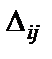выбираем наибольшую по абсолютному значению. Обозначим выбранную оценку через .

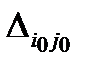7. Для клетки с выбранной оценкой 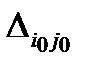строим прямоугольный контур, состоящий горизонтальных и вертикальных отрезков, которые пересекаются под прямым углом. Одна вершина контура должна находиться в свободной клетке с номером ( 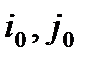), а все остальные в занятых клетках.

8. Начиная с ( 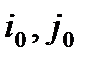) вершинам контура присваиваем знаки «плюс» и «минус».

9. Среди вершин контура со знаком «минус» выбираем наименьшее значение и обозначим ее q.

10. Передвигаем величину q по контуру, прибавляя ее к поставкам, находящимся в вершинах со знаком «плюс», и вычитаем из поставок, стоящих в вершинах, имеющих знак «минус».

Получаем новый опорный план. Возвращаемся к шагу 3.

Замечание 2: Если в вершинах контура со знаком «минус» имеется две (или несколько) одинаковых наименьших поставок q, то при перераспределении поставок по контуру (чтобы избежать вырожденности плана) необходимо в одну или несколько из этих вершин записать нуль–поставку (предпочтение отдается той вершине которая соответствует клетке с наилучшим ).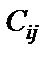

Замечание 3: Подсчитав значение линейной формы для первоначального опорного плана по формуле:

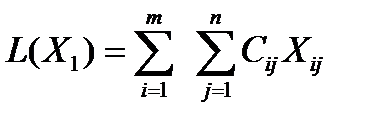
последующие значения L(X) можно вычислять по формуле

,

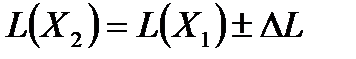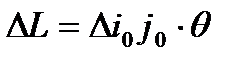
где «плюс» (если задача решается на максимум), и «минус» (если задача решается на минимум).

Замечание 4: Если при полученном оптимальном плане имеются нулевые оценки свободных клеток, то задача имеет множество оптимальных планов. Для клетки с нулевой оценкой нужно построить контур и сделать перераспределение поставок, вновь полученный план также будет являться оптимальным. Тогда по основной теореме ЛП любой план 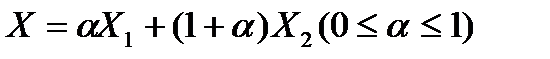будет оптимальным.

Пример. Найти план перевозок, чтобы общая стоимость была минимальной, при следующих данных.

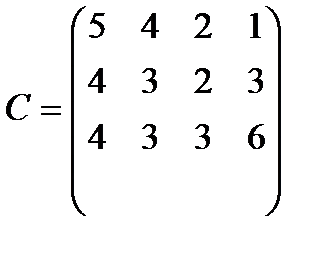a₁=4, a₂=8, a₃=8; b₁=7, b₂=3, b₃=6, b₄=6.

1. Проверяем условие разрешимости:

; .

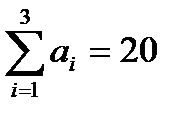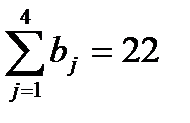Вводим фиктивного поставщика А_ф с ресурсами a_ф=22-20=2.

2. Строим первоначальный опорный план методом наилучшего элемента матрицы (таблица 1.6.). Наименьшая стоимость С₄₁=0, направляем в клетку (4,1) поставку x₄₁=min(2,7)=2. Все ресурсы А_ф исчерпаны, поэтому эту строку зачеркиваем. Из оставшихся стоимостей наименьшая С₁₄=1, тогда x₁₄=min(8,4)=4 и т.д. Процесс продолжается до полного распределения ресурсов. Получим следующий план

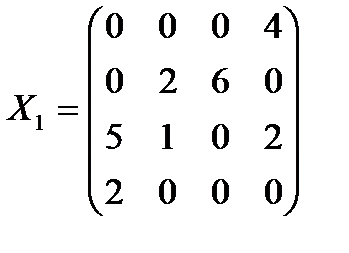
3. Полученный план невырожденный, т.к. m+n-1=7 и число занятых клеток в таблице 1.6. равно 7.

4. .

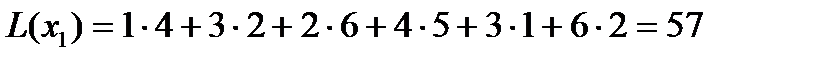5. Проверяем условие оптимального плана. Для занятых клеток строим систему :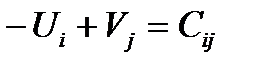

(1,4): ;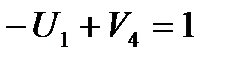

(2,2): ;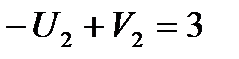

(2,3): ;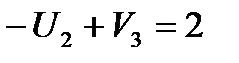

(3,1): ;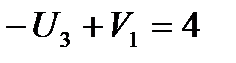

(3,2): ;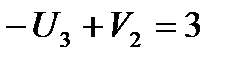

(3,4): ;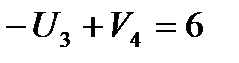

(4,1): .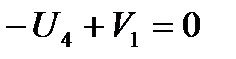

Полагаем 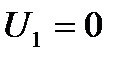находим все значения:

.

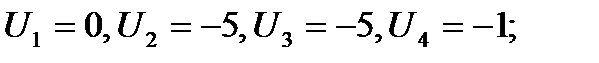
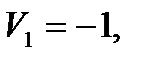
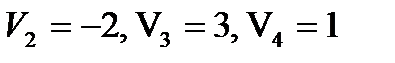Заполняем в таблице 1.6. столбец 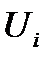и строку 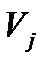. Находим оценки свободных клеток,

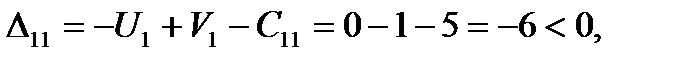
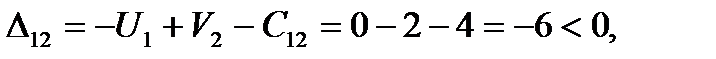
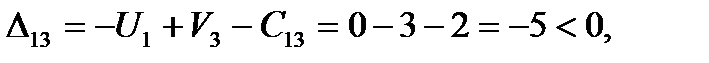
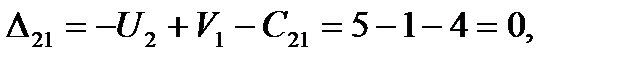
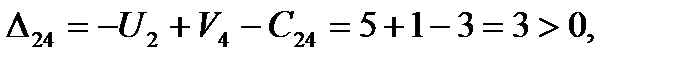
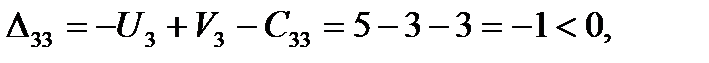
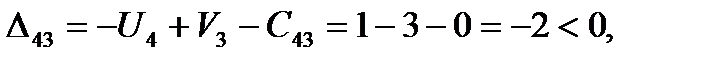
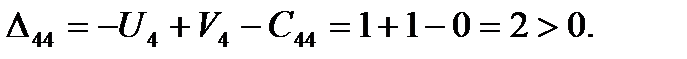
6. План Х₁ –неоптимальный, т.к. имеются положительные оценки свободных клеток. Выбираем из них наибольшую .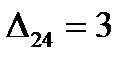

7. Для клетки с номером (2,4) строим контур. Вершины контура: (2,4), (3,4), (3,2), (2,2).

8. Расставляем знаки по вершинам начиная с (2,4).

9. Среди поставок стоящих в клетках (2,2) и (3,4), выбираем наименьшую: .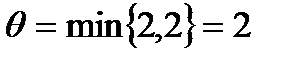

10. Перемещаем 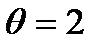по контуру, прибавляя ее к поставкам в клетках (2,4) и (3,2), и отнимая от поставок в клетках (2,2) и (3,4).

Получим новые поставки: 3 – в клетке (3,2), 2 - в клетке (2,4), а клетки (2, 2) и (3,4) становятся свободными. Имеем случай вырождения (Замечание 2). В клетку с номером (2,2) (т.к.С₂₂<С₃₄) вставим нуль поставку. Новый опорный план записываем в таблицу 1.7., переходим к шагу 3.

3. Новый план,

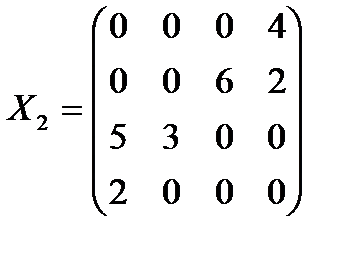
4. .

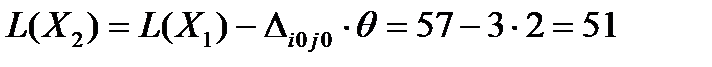5. Проверяем оптимальность плана.

Для занятых клеток:

(1,4): ;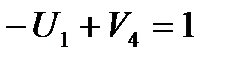

(2,4): ;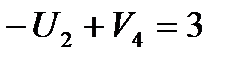

(2,3): ;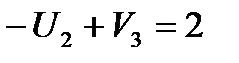

(2,2): ;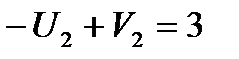

(3,1): ;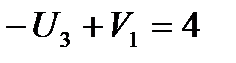

(3,2): ;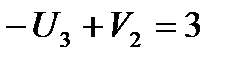

(4,1): .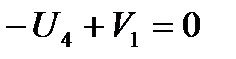

Отсюда:

.

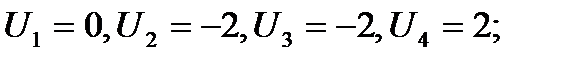
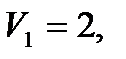
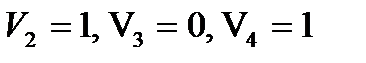Для свободных клеток:

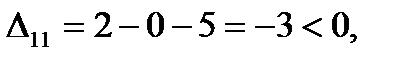
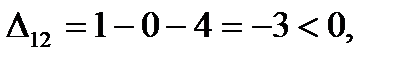
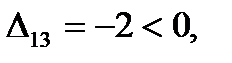
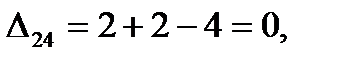
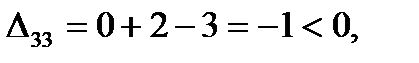
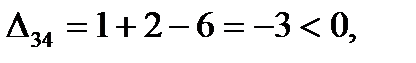
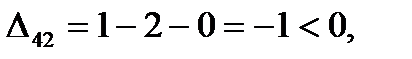
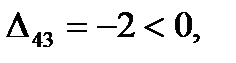
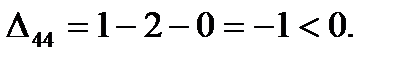
Следовательно, план Х₂ оптимальный. Выписываем его (поставка по дополнительной строке не заносится) и значение линейной формы.

, .

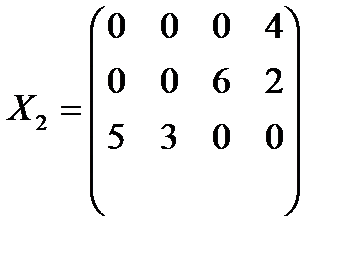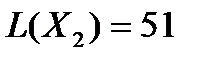Так как 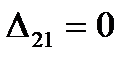, то задача имеет множество оптимальных планов. Для клетки (2,1) можно построить контур и сделать перераспределение поставок. Получим Х₃, который так же является оптимальным и 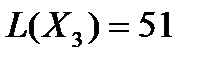. Тогда по основной теореме ЛП любой план 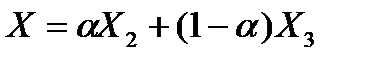, где 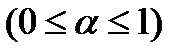, является также оптимальным планом задачи [3].

Таблица 1.6

Вj Ai		B1	B2	B3	B4	Ресурсы
	Vj Ui	V1=-1	V2=-2	V3=-3	V4=1
А1	U1=0
А2	U2=-5		- 3		+ 3
A3	U3=-5		+ 3		- 6
А4	U4=-1
Потребности						20+2

Таблица 1.7

Вj Ai		B1	B2	B3	B4	Ресурсы
	Vj Ui	V1=2	V2=1	V3=0	V4=1
А1	U1=0
А2	U2=-2
A3	U3=-2
А4	U4=2
Потребности