Построение перпендикуляра к плоскости, проходящего через заданною точку
Известно, что прямая перпендикулярна к плоскости, если она перпендикулярна к двум пересекающимся прямым этой плоскости. При построении перпендикуляра в качестве таких двух пересекающихся прямых плоскости используются линии уровня плоскости (фронтали и горизонтали). Это связано с тем, что согласно теоремы о проецировании прямого угла, именно с этими прямыми сохраняется прямой угол на плоскостях проекциях.
Пример построения перпендикуляра к плоскости, проходящего через заданною точку (рис. 59).
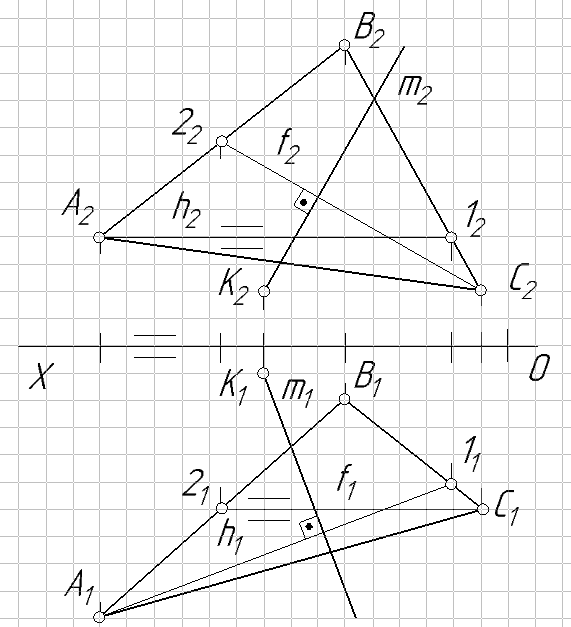
Рис. 59
Постановка задачи. Задана плоскость α треугольником ∆АВС и точка К. Построить перпендикуляр т к плоскости α, проходящей через точку К. Координаты точек: А(75; 50; 20), В(30; 10; 55), С(5; 30;10) и К(45; 5; 10).
Решение.
1. В плоскости α проводится горизонталь h: hÌα и h‖π1.
2. Используя теорему о прямом угле строится первая проекция перпендикуляра m: m1⊥h1 и К1⊂m1.
3. В плоскости α проводится фронталь f: fÌα и f‖π2.
4. Используя теорему о прямом угле строится вторая проекция перпендикуляра m: m2⊥f2 и К2⊂m2.
Варианты заданий приведены в табл. 9.
Построение прямой параллельной заданной плоскости
Известно, что если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна самой плоскости.
Построение прямой параллельно заданной плоскости основывается на использовании этого утверждения и инварианта параллельности прямых.
Пример построения (рис. 60).
Постановка задачи. Задана плоскость α треугольником ∆АВС и точка М не принадлежащая этой плоскости. Координаты точек: А(75; 50; 20); В(30; 10; 55); С(5; 30;10) и М(45; 30; 30).
Построить прямую l параллельную плоскости α, проходящую через точку М.
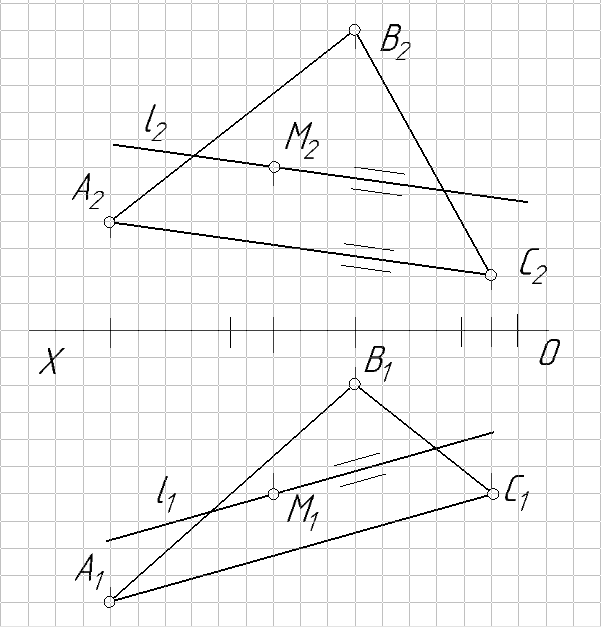
Рис. 60
Решение.
1. В заданной плоскости α выбирают или строят прямую, которая принадлежит этой плоскости (в примере выбрана сторона АС треугольника ∆АВС).
2. Используя инвариант параллельности прямых через проекции точки M проводят проекции искомой прямой l: М1⊂l1 и l1∥A1C1; М1⊂l1 и l1∥A1C1.
Варианты заданий приведены в табл. 9.
Таблица 9
Исходные данные по темам «Перпендикулярность и параллельность прямой и плоскости»
| Вариант | Численные значения координат точек | ||||||||||||||
| А | В | С | К | М | |||||||||||
| x | y | z | x | y | z | x | y | z | x | y | z | x | y | z | |
продолжение табл. 9
| Вариант | Численные значения координат точек | ||||||||||||||||||||||||||||||
| А | В | С | К | М | |||||||||||||||||||||||||||
| x | y | z | x | y | z | x | y | z | x | y | z | x | y | z | |||||||||||||||||
