Частотные характеристики интегрирующего звена

Из передаточной функции (4) звена W(p) = k/p определяем:

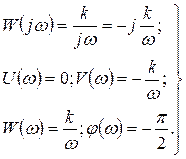(31)

Согласно формуле 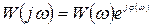получим также:

.

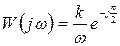(32)

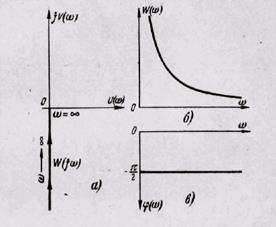Частотные характеристики представлены на рис. 13, из которого следует, что

а) АФХ звена W(jω) при изменении ω от 0 до ∞ со­впадает с отрицательной мнимой полуосью (рис. 13,а);

б) при всех частотах выходные колебания отстают по фазе от входных на угол 90° (рис. 13,в);

в) АЧХ представляет собой гиперболу, т.е. чем мень­ше частота входного сигнала, тем больше этот сигнал
усиливается звеном. При ω = 0 коэффициент усиления равен бесконечности и наоборот, при ω = ∞ коэффи­циент усиления звена равен нулю (рис. 13,б).

Логарифмируя W(ω) в (31), получим:

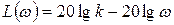. (33)

Таким образом, ЛАЧХ представляет собой прямую линию, пересекающую при k = 1 ось абсцисс в точке ω = 1 и имеющую наклон к оси абсцисс 20 дб/дек. При k ≠ 1 ЛАЧХ перемещается параллельно оси ординат на величину 201gk (рис. 14,а).

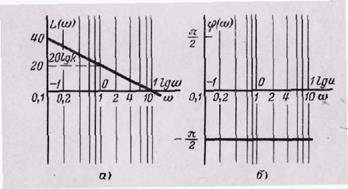Логарифмическая фазо-частотная характеристика не зависит от частоты и равна -π/2 (рис. 14,б). На рис. 14 на оси абсцисс для сравнения указаны значения как ω, так и lgω, а также нанесена координатная сетка частот.

8.3. Частотные характеристики апериодического звена

Из передаточной функции звена W (р) = 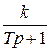[фор­мула (10)] находим его АФХ:

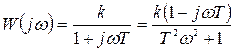. (34)

Вещественная и мнимая частотные характеристик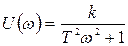и

и 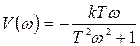. (35)

Согласно уравнениям 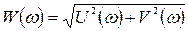и 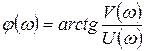АЧХ и ФЧХ имеют вид:

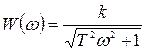; (36)

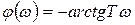. (37)

Задаваясь различными значениями ω, можно по вы­ражениям (34) построить АФХ звена. Однако в дан­ном случае можно из этих же двух уравнений алгебраи­чески получить на плоскости U, jV уравнение кривой W(jω) в явной форме как функцию.

Складывая выражения (35), получим:

.

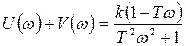Возведя в квадрат левую и правую части равенства, найдем;

,

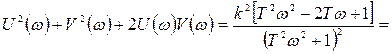
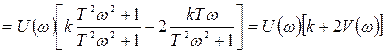откуда

.

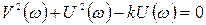Прибавляя к обеим частям этого равенства слагаемое (k/2)², получаем:

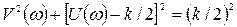. (38)

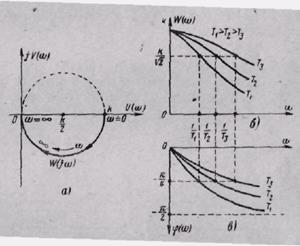Из полученного уравнения следует, что АФХ имеет вид окружности (рис. 15,а) с радиусом k/2, центр ко­торой расположен на положительной вещественной полуоси в точке с координатами (k/2; 0). Окружность ка­сается мнимой оси в начале координат. Изменениям ω от 0 до +∞ соответствует полуокружность, расположен­ная в четвертом квадранте, а изменениям ω от 0 до - ∞ - полуокружность в первом квадранте.

На рис. 15,б и в представлены также амплитудно-частотная и фазово-частотная характеристики звена. Из графиков частотных характеристик видно, что усиление звена по амплитуде при увеличении частоты уменьшает­ся. Это уменьшение тем резче, чем больше постоянная времени.

С ростом частоты увеличивается также фазовый сдвиг выходных колебаний по отношению к входным. Фазо-частотная характеристика звена отрицательна, сле­довательно, выходные колебания по фазе отстают от входных. При одной и той же частоте фазовый сдвиг тем больше, чем больше постоянная времени звена. При небольших частотах (ω ≈ 0) апериодическое звено ведет себя как усилительное звено с коэффициентом усиления k. При больших частотах выходная величина по модулю стремится к нулю, а ее фаза φ(ω) - к значению -π/2.

При ω = 1/T фаза φ(ω) = -π/4, a W(ω) = .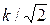

Логарифмируя выражение (36), найдем:

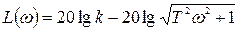. (39)

Из выражения (39) следует, что при изменений коэффициента усиления звена ЛАЧХ перемещается па­раллельно оси ординат, не меняя своей формы. При из­менении частоты от 0 до ∞ при ω << 1/T ЛАЧХ можно аппроксимировать горизонтальной прямой L(ω) = 201gk, а при ω>>1/T - прямой L(ω) = 20lgk–20lgωT, имею­щей наклон - 20 дб/дек.

Действительно, например, при ω₁, ЛАЧХ равна L(ω₁) = 20lgk – 20lgω₁T, а при ω₂ = 10ω₁ получаем L(ω₂)=20Igk - 20lg10ω₁T. Найдем уменьшение ЛАЧХ на декаду:

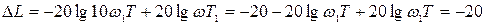дб/дек.

Следовательно, ЛАЧХ может быть приближенно представлена двумя вышеуказанными прямыми (асимп­тотами), сопрягающимися друг с другом при частоте ω₁ = l/Т. Эту частоту принято называть сопрягающей. При представлении фактической ЛАЧХ приближенной (рис. 16,а) максимальная ошибка будет на сопрягаю­щей частоте

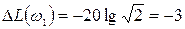дб.

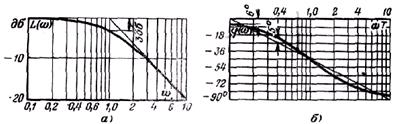Логарифмическая фазо-частотная характеристика, построенная в полулогарифмическом масштабе по выра­жению (37), представляет собой кососимметричную линию (рис. 16,б). На интервале частот 0,1/Т < ω < 10/Т ЛФЧХ можно аппроксимировать прямой с наклоном - 45°/дек, проходящую через точку с координатами [φ(ω) = 45°; ωТ = 1 дб]. При этом следует отметить, что при такой аппроксимации ошибка является существен­ной (до 6°), в связи с чем она не всегда допустима.