Автоматов в нейросетевом базисе

Развитие современных вычислительных систем в направлении цифровых архитектур параллельного действия, а также нейроархитектур, реализующих существенный параллелизм вычислений в нейросетевом логическом базисе, ставит в разряд наиболее актуальных проблемы формализации задач под выбранную архитектуру вычислительной системы.

Цифровые автоматы как объект исследования представляют интерес в двух аспектах. Во-первых, как средства технического обеспечения информационных систем различного назначения (САПР, АСУ, АСНИ, АОС и т.д.). Во-вторых, как объект проектирования в САПР микроэлектронных устройств цифровой аппаратуры.

Постоянное совершенствование архитектуры цифровых ВС, усложнение их конструктивно-технологической базы, использование цифровых модулей в реализациях нейрокомпьютеров предъявляют особые требования к методам и технологиям их проектирования. Развитие этих методов в свою очередь способствует появлению и внедрению в вычислительную практику новых архитектурных решений.

Методы проектирования произвольных цифровых автоматов с памятью исходят из основных положений абстрактной теории автоматов и более конструктивного ее продолжения — структурной теории автоматов [10]. На абстрактном уровне достаточно просто решаются вопросы определения числа состояний автомата (с возможностью его минимизации) и необходимого для их фиксации объема памяти. Согласно структурной теории, синтез логической схемы (структурный синтез) произвольного конечного автомата сводится к структурному синтезу схемы (схем) комбинационной логики. При этом в качестве исходной для синтеза комбинационной схемы выступает функциональная таблица автомата, сформированная по несложным правилам в соответствии с выбранным типом запоминающих элементов памяти и алгоритмом функционирования автомата, представленным его структурными таблицами переходов и выходов. Функциональная таблица представляет собой таблицу истинности, содержащую значения реализуемых логических функций (выходов комбинационной схемы) для всех наборов их аргументов (входных сигналов комбинационной цепи).

Традиционные методы синтеза комбинационных схем предполагают дальнейший переход от таблицы истинности к СДНФ (СКНФ) реализуемых функций, их оптимизацию по определенным критериям и реализацию в заданном логическом базисе [10, 18]:

· на основе программируемой логической матрицы или матричной логики;

· в виде логического блока табличного типа;

· на основе универсального логического модуля (мультиплексора);

· в малом логическом базисе (на вентильном уровне).

Синтез комбинационной схемы в малом логическом базисе (SLC – Simple Logic Cells) предоставляет широкие возможности для поиска наиболее рациональных решений. Однако традиционные методы минимизации булевых функций не являются универсальными с точки зрения произвольного выбора малого логического базиса для синтеза схем. Они оперируют в классе ДНФ (КНФ) булевых функций, не предусматривая возможность одновременной (согласованной в соответствии с дополнительными критериями) минимизации системы функций. С увеличением размерности пространства переменных (аргументов) функции становятся громоздкими и трудно контролируемыми. Процесс носит эвристический характер и порождает обширное множество вариантов схем, среди которых не всегда оказываются лучшие.

Развитие и внедрение в практику нейросетевой вычислительной парадигмы привело к появлению нового типа представления задач. К традиционным перечисляющему представлению, представлению в пространстве состояний, иерархическому представлению и их комбинациям добавилось представление задач в нейросетевом базисе. Оно позволяет:

· выделить естественный для данного представления существенный параллелизм задачи;

· применить для ее формализации известные методы обучения искусственных нейронных сетей;

· определиться с архитектурой ВС, наиболее рациональной для решения рассматриваемого класса задач.

В работе [3] показана возможность представления комбинационной логической схемы эквивалентной (бинарной или биполярной) нейронной сетью прямого распространения (с сохранением физического и математического смысла всех параметров). Это позволяет свести трудноформализуемую проблему синтеза схем произвольной комбинационной логики к формальной задаче обучения (оптимизации) исходно избыточной нейронной сети с распараллеливанием вычислений (анализа нейронной сети) на каждой итерации оптимизационного процесса.

Синтезируемая комбинационная схема представляется в виде многослойной нейронной сети прямого распространения - многослойного персептрона, составными элементами которого являются спецпроцессоры двух видов:

· нейроны, преобразующие поступающие на их входы бинарные (принимающие значения 0 или 1) или биполярные (принимающие значения 1 или -1) сигналы в единственный выходной сигнал в соответствии с заданной активационной функцией нейрона (ступенчатой или биполярной ступенчатой);

· связи между нейронами, реализующие межнейронные взаимодействия в виде бинарных (или биполярных) сигналов, умножаемых на синаптические веса связей.

Исходно персептрон имеет все возможные межнейронные связи, не нарушающие его свойство прямонаправленности (каждый нейрон предшествующих слоев имеет непосредственные связи воздействия на все нейроны последующих слоев и ни на какие другие). Количество входов персептрона равно числу аргументов 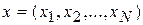реализуемых логических функций, а количество выходов — числу реализуемых функций 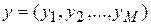. Число внутренних (скрытых) слоев и количество нейронов в каждом из них задаются эвристически.

Виды активационных функций нейронов, их пороги и возможные значения синаптических весов межнейронных связей определяются выбором конкретного базиса SLC. Так, в случае базиса {И, ИЛИ, НЕ}, нейроны имеют биполярную ступенчатую активационную функцию

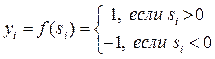, (8.1)

где 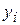— сигнал на выходе 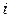-го нейрона; ;

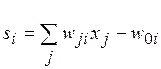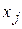— сигнал на выходе 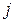-го нейрона, воздействующего на 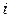-й нейрон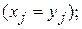

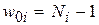— порог активационной функции 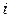-го нейрона, реализующего логическую функцию И;

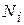— общее количество нейронов, непосредственно воздействующих на 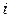-йнейрон;

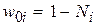— порог активационной функции 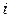-го нейрона, реализующего логическую функцию ИЛИ.

Синаптические веса межнейронных связей могут принимать значения 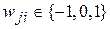. Значение 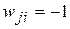представляет связь через инвертор (логическую функцию НЕ), 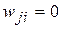отмечает отсутствие данной связи между нейронами, 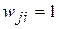определяет обычную ретрансляционную связь.

Сигналы, распространяющиеся в данной сети, принимают значения из .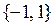

В случае использования базисов {И-НЕ}, {ИЛИ-НЕ} нейроны имеют, соответственно, активационные функции следующих видов:

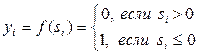; (8.2)

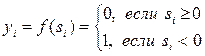, (8.3)

где 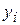— сигнал на выходе 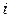-го нейрона;

;

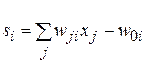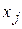— сигнал на выходе 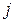-го нейрона, воздействующего на 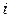-й нейрон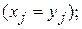

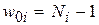— порог активационной функции (8.2) 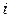-го нейрона, реализующего логическую функцию И-НЕ;

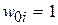— порог активационной функции (8.3) 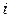-го нейрона, реализующего логическую функцию ИЛИ-НЕ.

Синаптические веса межнейронных связей могут принимать значения 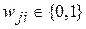. Значение 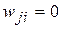отмечает отсутствие данной связи между нейронами, 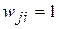определяет обычную ретрансляционную связь.

Сигналы, распространяющиеся в данной сети, принимают значения из .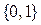

При обучении нейронной сети в качестве варьируемых параметров выступают типы активационных функций нейронов (только для базиса {И, ИЛИ, НЕ}) и синаптические веса межнейронных связей.

Роль множества обучающих шаблонов 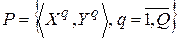выполняет исходная таблица истинности, т.е. функциональная таблица автомата 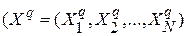— 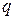-й вектор известных значений аргументов реализуемых функций, 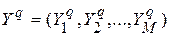— вектор соответствующих значений функций, 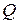— мощность обучающего множества, т.е. число строк таблицы истинности, равное 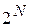для полностью определенных функций).

В процессе обучения векторы 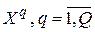, из множества 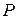последовательно подаются на вход персептрона и для каждого из них оценивается ошибка между фактическим 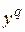и желаемым 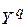откликом (выходом) сети 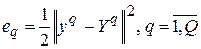. Затем определяется общая ошибка 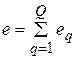, на основании которой алгоритм обучения осуществляет модификацию значений настроечных параметров сети, направленную на уменьшение ошибки. Обучение продолжается до тех пор, пока сеть не приобретет способность выполнять требуемый тип преобразования, заданный набором шаблонов 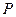(об этом свидетельствует значение ошибки ).

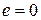С математической точки зрения рассмотренная задача обучения персептрона представляет собой однокритериальную задачу дискретной безусловной оптимизации (минимизации). Поэтому для ее решения в работах [3, 4] применены эволюционно-генетические алгоритмы [6, 9] и метод имитации отжига.

В ходе эволюции персептрона избыточной структуры последовательно получаются все допустимые в ее рамках эквивалентные варианты нейронных сетей, реализующие исходную таблицу истинности (для них ошибка 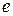на выходе должна быть нулевой). Среди этих вариантов возможно присутствие идентичных структур, построенных на различных наборах нейроэлементов (число таких структур напрямую зависит от степени избыточности исходного персептрона). Из них для дальнейшего рассмотрения оставляется только одна.

В потенциале данный подход позволяет получить весь спектр решений поставленной задачи синтеза, возможный для заданной начальной топологии нейронной сети. Из него могут быть выбраны те, которые обеспечивают приемлемый компромисс в пространстве критериев быстродействия, аппаратной сложности, технологичности исполнения схемы и др.

Рассмотренный подход отличается высокой степенью формализма, недостижимой для классической теории синтеза комбинационных схем [10]. Он покрывает единым образом как общую классическую задачу синтеза, так и все ее частные классы (с дополнительными условиями в различных сочетаниях), в том числе каноническую задачу комбинационного синтеза. В отличие от классического, данный подход позволяет осуществлять синтез многофункциональных (векторных) устройств произвольной комбинационной логики в различных функционально полных базисах, что обусловливает возможность использования его при решении проблем интеграции схем.