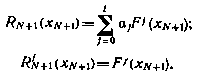Учёт изоперимётричёских ограничений

При, решении практических задач синтеза оптимального управления часто приходится учитывать кроме ограничений, на­кладываемых на вектор управления, дополнительные ограничения вида

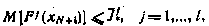
где 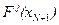—известные функции вектора 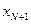; 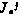— некоторые заданные величины, l—количество ограничений. Такие ограниче­ния в дальнейшем называются изопериметрическими.

Задача формулируется следующим образом. Требуется найти такой алгоритм управления системой

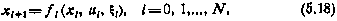
который, обращая в минимум критерий,

удовлетворял бы ограничениям

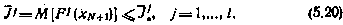
Для учета последних обратимся к методу обобщенных множи­телей Лагранжа. Составим обобщенный критерий оптимальности

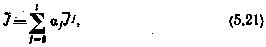
где 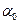— множители Лагранжа, один из которых для определенно­сти, например 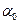, равен единице.

В соответствии с известными необходимыми условиями опти­мальности (теорема Куна — Таккера) [28] условная минимизация критерия (5.19) с учетом (5.20) может быть заменена безусловной минимизацией обобщенного критерия (5.21), если множители Ла­гранжа 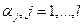определить как неотрицательные корни, 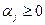, системы уравнений

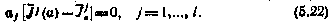
Здесь под 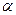понимается вектор с компонентами 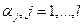. Уравнения (5.22) следует понимать таким образом, что либо 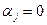, если 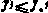, либо 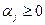, если 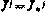. Если же при всех 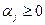име­ет место неравенство 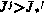решения задачи не существует, так как ограничение 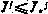не может быть выполнено.

Следует заметить, что в случаях, когда ограничения (5.20) вы­полняются в виде строгих равенств, то существование 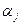, при кото­рых эти равенства имеют место и одновременно обеспечивается ми­нимум обобщенного критерия оптимальности, является достаточ­ным условием того, чтобы основной критерий также достигал минимума.

Действительно, допустим, что существуют такие множители щ, при которых управляющая последовательность 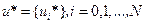, обращает критерий (5.21) в минимум

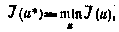
и имеют место равенства

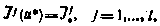
Тогда для любых и имеет место неравенство

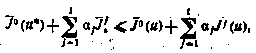
откуда

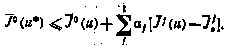
Но последнее условие и означает, что управление и* обеспечи­вает минимум критерия 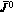при условии .

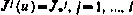Общая последовательность решения задачи теперь сводится к следующему. Из условия минимизации обобщенного критерия на­ходим структуру оптимального управления. Для этого по-прежне­му используем основное рекуррентное соотношение (5.7):

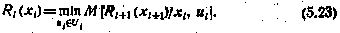
Однако граничное условие (5.8) в соответствии с (5.19) — (5.21) принимает теперь вид

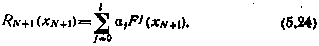
Нетрудно видеть, что получаемый при этом алгоритм оптималь­ного управления оказывается зависящим от вектора множителей Лагранжа 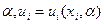. Для определения компонент 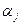необхо­димо обратиться к условиям (5.22), раскрыв предварительно в них зависимости 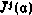. С этой целью, полагая, что структура оптималь­ного управления 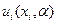определена, введем в рассмотрение функ­ции 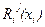аналогично функции будущих потерь:

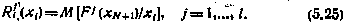
В выражениях (5.25) отсутствует лишь операция минимизации по управлению. Функция 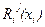представляет собой фактически величину 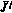, вычисленную при условии, что движение системы (5.18) начинается с момента i из состояния и происходит с вы­бранным уже алгоритмом оптимального управления. Очевидно, функции 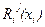через алгоритм управления также зависят от век­тора 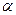, т. е. 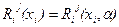. Полагая в (5.25) i = 0, получаем

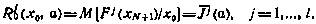
С учетом этих соотношений система (5.22) для определения 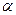может быть представлена теперь в виде

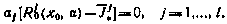
Выясним теперь, каким образом можно найти функции 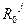. Из выражения (5.25) следует, что

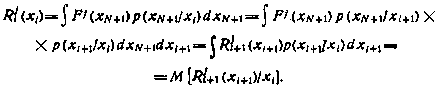
Следовательно, каждая функция 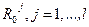, может быть опре­делена с помощью рекуррентного соотношения

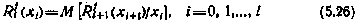
с граничным условием

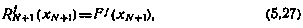
получаемым сразу из (5.25), если принять i=N+1.

Таким образом, определение оптимального управления в дан­ной задаче сводится к применению основного рекуррентного соот­ношения (5.23) с граничным условием (5.24) для выявления структуры этого управления, к применению рекуррентных соотношений (5.26)_с граничными условиями (5.27) для установления зависимо­стей 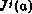при разных j и последующего решения системы (5.22) относительно вектора а.

Как и прежде, нетрудно показать, что если критерий оптималь­ности имеет вид

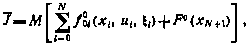
а дополнительные ограничения вид

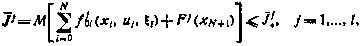
то при определении структуры оптимального управления вместо рекуррентного соотношения (5.23) следует применять соотношение

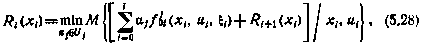
а при раскрытии зависимостей 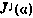вместо рекуррентных соотно­шений (5.26) — соотношения

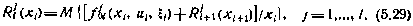
Граничные условия (5.24), (5.27) при этом сохраняются прежни­ми, т. е.