Корреляционная теория случайных процессов

При практических расчетах для описания случайных процессов, как и для описания случайных величин, часто пользу­ются их моментными характеристиками.

Простейшей моментной характеристикой случайного процесса x(t) является математическое ожидание m_x(t), представляющее собой неслучайную функцию времени t. Если известна одномерная плотность вероятности р(х, t), то m_x(t) можно рассчитать для каж­дого t с помощью формулы, аналогичной (1.12):

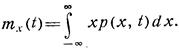
Математическое ожидание m_x(t) характеризует лишь среднее течение случайного процесса x(t) по времени. Оно не содержит в себе информацию ни о том, каково рассеивание возможных реали­заций процесса x(t) относительно его математического ожидания m_x(t), ни о степени статистической взаимосвязи (корреляции) воз­можных реализаций процесса в различные моменты времени.

Для описания вероятностной зависимости между возможными реализациями случайного процесса x(t) в различные моменты вре­мени используют его корреляционную функцию. Так называемые не­случайную функцию R_x(t₁, t₂) двух неслучайных аргументов t₁ и t₂, определяемую следующим образом:

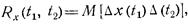
где 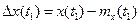; 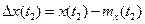- центрирован­ные случайные величины, соответствующие x(t) при t=t₁ и t=t₂.

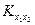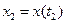Таким образом, корреляционная функция R_x(t₁, t₂) случайного процесса x(t)—это взаимный корреляционный момент меж­ду случайными величинами и , зависящий от ар­гументов t₁ и t₂.

Если совместная двумерная плотность 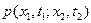случайного процесса x(t) известна, то корреляционную функцию данного про­цесса можно определить с помощью соотношения, аналогичного (1.16):

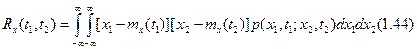
По имеющимся реализациям оценку 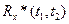корре­ляционной функции можно рассчитать с помощью формулы мате­матической статистики

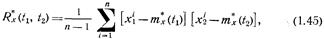
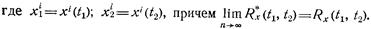
Если аргументы t₁ и t₂ в корреляционной функции совпадают, т. е. t₁ и t₂=t, то, учитывая предельное свойство (1.35), из соотно­шения (1.44) получаем

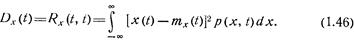
Корреляционная функция 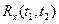при совпадающих аргумен­тах есть не что иное, как дисперсия случайной величины х, полу­чаемой из случайного процесса x(t) путем фиксации аргумента t. Дисперсия D_x(t) характеризует рассеивание возможных реализа­ций процесса x(t) в окрестности его математического ожидания m_x(t).

Корреляционную функцию 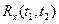, отнесенную к произведе­нию 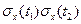, называют нормированной корреляционной функ­цией 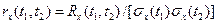. При t₁ и t₂=t нормирован­ная корреляционная функция r_x(t) равна единице. Равенство нулю 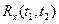или 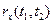указывает на отсутствие корреляции между возможными реализациями случайного процесса x(t) в моменты t₁ и t₂. Как правило, по мере увеличения интервала 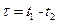кор­реляция между возможными реализациями случайного процесса x(t) убывает. Корреляционная функция 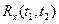процесса при этом меняется от 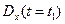до нуля, a 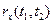- от 1 до 0.

Результат усреднения в (1.43) не зависит от того, в какой по­следовательности рассматриваются 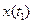и 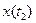, поэтому корреля­ционная функция не меняется при перемене аргументов местами: .

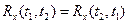Изучение свойств случайных процессов на уровне их первых двух моментов (математического ожидания m_x(t) и корреляцион­ной функции 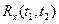называют корреляционной теорией случай­ных процессов. В рамках корреляционной теории случайный процесс x(t) описывается полностью, если этот процесс — гауссовский.

Корреляционная теория распространяется и на векторные слу­чайные процессы. Если x(t)—векторный процесс, объединяющий п компонент , то в рамках корреляционной теории этот процесс описывается вектором математических ожиданий 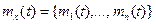и матричной корреляционной функцией

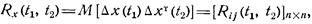
где 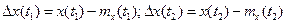— центрированные случайные векторы. Диагональные элементы 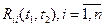, матричной корреляционной функции называют автокорреляционны­ми функциями соответствующих компонент векторного случайного процесса x(t), а внедиагональные 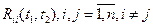- взаим­ными корреляционными функциями компонент 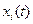и .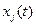

При t₁ = t₂=t матричная корреляционная функция векторного случайного процесса x(t) обращается в его корреляционную матри­цу K_x(t), характеризующую вероятностную зависимость между компонентами вектора х в момент времени t.