Методы статистического описания случайных величин, процессов и полей

ББК 39.52

Т5.1

Издательство «Машиностроение», 1985 г.

ПРЕДИСЛОВИЕ

Учебное пособие предназначено для студентов вузов, изучающих дисциплины «Статистическая динамика летательных аппаратов», «Оптимальное управление летательными аппаратами», «Системы управления летательных аппаратов» и близкие к ним по содержанию. Содержание первых двух дисциплин включает в себя изложение основ теории динамических систем при действии слу­чайных возмущений и теории оптимального управления детермини­рованными и стохастическими динамическими системами. Третья дисциплина в значительной степени прикладная и базируется на первых двух.

Учебное пособие содержит материал, относящийся главным об­разом к первым двум дисциплинам. Оно может быть также исполь­зовано при изучении дисциплины «Системы управления летатель­ных аппаратов», поскольку содержит ряд конкретных технических примеров применения современных статистических методов и мето­дов оптимизации для синтеза систем управления полетом.

При пользовании данным пособием читателю необходима под­готовка в объеме вузовской программы по таким дисциплинам, как «Теория автоматического управления», «Динамика полета лета­тельных аппаратов», «Основы теории вероятностей и математичес­кой статистики», «Основы теории оптимального управления».

Авторы будут признательны всем читателям, которые пришлют критические замечания по содержанию книги.

ВВЕДЕНИЕ

Проектирование современных высокоточных систем уп­равления в значительной степени связано с проблемой синтеза оп­тимальных стохастических систем. В эту проблему входят задачи, связанные с определением показателей функционирования систем в условиях случайных возмущений, т. е. с их статистическим анали­зом, задачи формирования оптимального управления такими систе­мами, а также задачи по переработке информации, доступной изме­рениям, в информацию, необходимую непосредственно для управле­ния. Следует отметить, что данной проблеме посвящено много работ. Однако основное внимание в них уделяется развитию общего тео­ретического аппарата применительно к задачам оптимизации си­стем, описываемых стохастическими дифференциальными уравне­ниями. Овладение этими методами, как правило, требует высокой математической подготовки и поэтому не всегда доступно инжене­рам, занимающимся проектированием реальных систем управле­ния.

Цель учебного пособия — систематическое изложение вопросов применения стохастической теории управления к решению задач анализа и синтеза систем управления летательными аппаратами различного назначения на уровне той математической подготовки, которая дается в технических вузах. Учитывая, что в настоящее время развитие систем управления вообще и систем управления ле­тательными аппаратами, в частности, характеризуется широким ис­пользованием цифровой вычислительной техники непосредственно в контуре управления, особое внимание в книге уделяется вопросам управления дискретными стохастическими системами.

Изложение большинства вопросов сопровождается примерами решения конкретных технических задач, связанных с анализом и синтезом систем управления летательными аппаратами.

Приводятся основные сведения из теории случайных величин, случайных процессов и случайных полей, необходимые для описа­ния и анализа стохастических систем. Рассматриваются вопросы моделирования реализаций случайных величин и процессов на ана­логовых и цифровых вычислительных машинах. Обсуждаются наи­более распространенные методы анализа точности систем управле­ния. Кратко излагаются метод переходных функций и частотный метод анализа точности линейных систем. Более подробно рассмот­рены вопросы применения метода статистической линеаризации и метода статистического моделирования для анализа точности нели­нейных систем. Значительное внимание уделено различным аспек­там практического использования методов анализа точности линей­ных и нелинейных систем, основанных на использовании теории мар­ковских процессов. Изложение рассматриваемых методов сопровождается примерами решения различных задач анализа точ­ности движения летательных аппаратов, таких, как движение в тур­булентной атмосфере, сближение космических аппаратов на орбите, самонаведение крылатого аппарата, баллистический спуск в атмос­фере и другие.

Рассматриваются задачи оптимизации стохастических систем управления. В качестве основного объекта исследования принимает­ся дискретная динамическая система. Исследуются задачи програм­мирования и синтеза оптимального стохастического управления. В первом случае предполагается, что текущая информация о состоя­нии объекта управления отсутствует. Во втором случае считается, что сигнал управления в каждый момент времени формируется на основе информации, полученной измерениями текущего состояния объекта. При этом различаются две ситуации: управление при пол­ной информации, когда считается, что текущее состояние объекта измеряется точно и полностью, и управление при неполной инфор­мации, когда измерительная информация не позволяет точно опре­делить текущее состояние объекта. Формулируются необходимые условия оптимальности, обсуждаются особенности применения чис­ленных методов математического программирования. Формулиру­ются достаточные условия оптимальности. Предлагается метод ре­шения задач при изопериметрических ограничениях. Обсуждаются различные приближенные методы синтеза оптимального управле­ния, основанные на обычной и статистической линеаризации, а так­же метод параметров и комбинированный метод. Приводятся примеры решения конкретных технических задач с использованием этих методов. Такими задачами являются задачи формирования алгоритмов управления при переводе стационарного спутника Земли на заданную долготу с помощью двигательной установки большой и малой тяги, при коррекции траектории движения космического аппарата.

Задача синтеза оптимального управления стохастическим объек­том при неполной информации рассматривается в байесовской по­становке с использованием метода динамического программирова­ния и понятия достаточных координат. Структура синтезируемой оптимальной системы представляется двумя последовательно соеди­ненными блоками: обработки информации и оптимального управле­ния. Для линейных моделей объекта управления, измерений и гаус-совских возмущений при квадратичном критерии оптимальности решение задачи синтеза обоих блоков осуществляется в явном виде. Для общего случая нелинейных моделей объекта управления и из­мерений предлагается синтезировать блок обработки информации, используя рекуррентные байесовские алгоритмы различной слож­ности.

ГЛАВА 1.

СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

Величина х, принимающая в каждом новом опыте при фиксированных условиях опыта новое значение хⁱ, где i — номер опыта, называется случайной. Значения хⁱ, i=1,2, ..., случайной ве­личины х, которые они принимают в отдельных опытах, называют реализациями случайной величины. Например, масса автоматиче­ского летательного аппарата в момент старта — случайная величи­на, изменения которой применительно к отдельным экземплярам (реализациям) аппарата обусловлены технологическими погрешно­стями его изготовления и подготовки к старту.

Моменты случайных величин

Моменты служат для описания основных свойств плотно­сти вероятности случайной величины. Они содержат меньше инфор­мации о случайной величине по сравнению с плотностью вероятно­сти, но часто более удобны при решении технических задач. В каче­стве моментов скалярной случайной величины чаще всего применяются математическое ожидание и дисперсия (или среднеквадратическое отклонение).

Математическим ожиданием некоторой функции y = f(x) случай­ной величины х называется интеграл

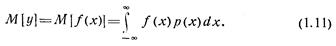
При f(x) = x^R величина M[x^R]=m_x^R называется начальным моментом R-го порядка случайной величины х. Начальный омент пер­вого порядка т_х называется математическим ожиданием случайной величины х:

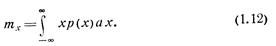
По реализациям 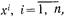математическое ожидание т_х может быть оценено как статистическое среднее

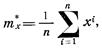
причем .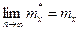

Разность 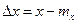менаду случайной величиной х и ее мате­матическим ожиданием т_х называется центрированной случайной величиной. Центральный момент R-го порядка скалярной случайной величины х определяется как математическое ожидание R-й степени соответствующей центрированной случайной величины:

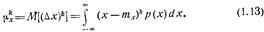
Центральный момент второго порядка 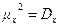называется дис­персией случайной величины х:

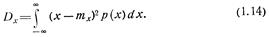
По реализациям 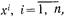оценку 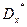можно рассчитать по формуле

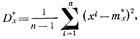
причем .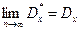

Дисперсия характеризует рассеивание значений случайной вели­чины х в окрестности ее математического ожидания т_х. Наряду с дисперсией D_x в качестве меры рассеивания рассматривают и среднеквадратическое отклонение .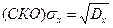

Центральные моменты высших порядков определяют аналогич­но. Например, центральный момент третьего порядка

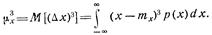
Он характеризует асимметрию кривой плотности вероятности р(х). Если р(x) —симметричная функция с осью симметрии, проходящей через т_х, то 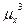, а также все другие нечетные центральные момен­ты случайной величины х равны нулю.

В качестве характеристик вероятностной зависимости двух ска­лярных случайных величин х и у рассматривают их корреляцион­ный момент

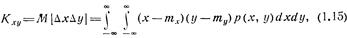
или коэффициент корреляции

вычисляемый при 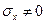и .

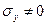По реализациям хⁱ, уⁱ, i= 1, п, случайных величин x и y их корре­ляционный момент можно оценить с помощью соотношения

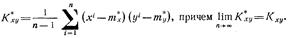
Если случайные величины х и у связаны между собой линейной зависимостью у = ах + b, где а и b — произвольные неслучайные числа, то 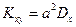, а r_xy=1 при а>1 и r_xy = -1 при а<0.

Случайные величины х и у называют некоррелированными, если 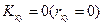. Используя формулы (1.15), (1.10), нетрудно пока­зать, что из независимости случайных величин следует их некорре­лированность. Обратное утверждение в общем случае неверно. Ина­че говоря, условие независимости случайных величин более сильное, чем условие некоррелированности.

Для векторной случайной величины х простейшими моментными характеристиками, наиболее часто рассматриваемыми при прак­тических расчетах, являются вектор математических ожиданий т_х и корреляционная матрица К_х- Составляющими вектора т_х являются математические ожидания компонент вектора х, т. е. .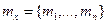

Корреляционной матрицей К_х случайного вектора х называется симметричная матрица, составленная из корреляционных моментов 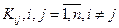, и дисперсий 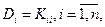составляющих век­тора х:

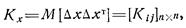
причем .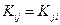

Если все составляющие случайного вектора х взаимно некорре­лированные, то этот вектор называют некоррелированным. Корре­ляционная матрица К_х некоррелированного вектора — диагональ­ная, все ее внедиагональные элементы равны нулю.

Нормальное распределение

Конкретный вид распределения случайной величины х зависит от физической природы явления. Особое место среди всевозможных распределений занимает распределение Гаусса или нормальное распределение, поскольку именно такими или близки­ми к нормальному являются распределения многих случайных ве­личин, рассматриваемых при анализе движения автоматических летательных аппаратов.

Нормальная плотность вероятности р_г(x) скалярной случайной величины х описывается выражением

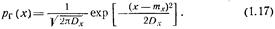
Она полностью характеризуется двумя параметрами: т_х и D_x. Пользуясь соотношениями (1.12) и (1.14), можно убедиться в том, что параметр т_х нормальной плотности вероятности есть математи­ческое ожидание, a D_x — дисперсия этой случайной величины.

В соответствии с формулой (1.2) вероятность попадания гауссовской случайной величины х в интервал 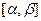равна

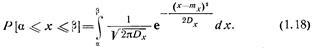
После замены переменной х на 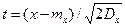вычисление интеграла в формуле (1.18) сводится к вычислению соотношения

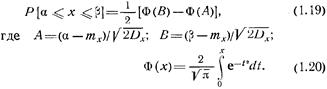
Значения функции Лапласа Ф(х), определяемой соотношением (1.20), приведены в приложении 1. При проведении расчетов на ЦВМ их можно рассчитать с помощью стандартной подпрограммы.

При преобразованиях выражений, содержащих функцию Лапла­са Ф(х), можно пользоваться следующими свойствами этой функ­ции:

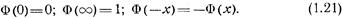
Нормальное распределение вероятностей n-мерного случайного век­тора х описывается формулой

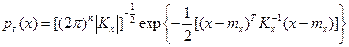
где т_х— вектор математических ожиданий; К_х — корреляционная матрица; 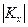- определитель корреляционной матрицы.

В евклидовом n-мерном пространстве, координатами которого являются составляющие вектора х, плотность вероятности р_г(х) постоянна на концентрических гиперэллипсоидах:

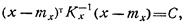
называемых гиперэллипсоидами рассеивания, где С — любое поло­жительное число. Центром гиперэллипсоидов рассеивания является точка с координатами т_х, направление главных осей совпадает с собственными векторами 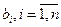корреляционной матрицы К_х, а длина каждой из главных полуосей равна 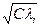, где 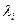— собствен­ное значение корреляционной матрицы К_х, соответствующее собст­венному вектору b_i.

В двумерном случае нормальное распределение (1.22) принима­ет вид

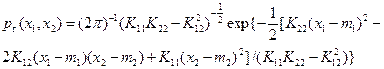(1.23)

Плотность вероятности (1.23) постоянна на эллипсах, называе­мых эллипсами рассеивания. Угол между главной осью эллипса рас­сеивания и осью Ox₁ определяется с помощью выражения [8]

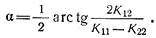
Если составляющие х₁ и х₂ вектора х некоррелированы, то на­правления главных осей эллипса рассеивания совпадают с направ­лениями осей системы координат Ох₁х₂.

На практике принято строить эллипсы рассеивания, главные по­луоси которых равны 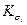где 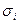— С КО соответствующей компо­ненты; К — целое число.

1.1.4. Линейные и нелинейные преобразования случайных величин

При решении задач статистического анализа и оптимиза­ции управления движением летательных аппаратов часто требуется определять моменты и распределения линейных и нелинейных функ­ций случайных величин. Например, при переходе от одной системы координат к другой требуется уметь вычислить вектор математиче­ских ожиданий и корреляционную матрицу фазового вектора, опи­сывающего состояние летательного аппарата относительно новой системы координат, если статистические характеристики фазового вектора относительно исходной системы координат известны.

Вначале рассмотрим случай линейного преобразования случай­ной величины. Пусть х и у — случайные векторы, связанные между собой линейным соотношением

где х — вектор размерности п; у — вектор размерности l; А — мат­рица размерности l×п; b — неслучайный вектор размерности l.

Используя соотношение (1.11) и учитывая (1.12), находим соот­ношение между т_х и т_у:

Вычитая (1.25) из (1.24), получаем соотношение 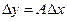между центрированными случайными величинами, из которого непосредст­венно вытекает соотношение между корреляционными матрицами К_x и К_у:

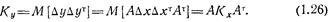
В частном случае при 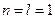, т. е. когда х и у— скалярные слу­чайные величины, имеем m_y=am_x+b; D_y=a²D_x. При п=2 и l=1, т. е. если y=a₁x₁ + a₂x₂ + b, получаем m_y = a₁m₁+ a₂m₂ + b и 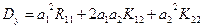, где K₁₁, K₁₂, K₂₂, - элементы корреляци­онной матрицы К_x-

В случае нелинейной зависимости y=f(x), где x — скаляр,

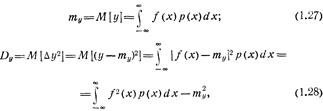
т. е. для нахождения m_y и D_y недостаточно знать т_х и D_x, а долж­на быть известна плотность вероятности р(х) аргумента х.

Пример.Рассмотрим преобразование гауссовской случайной величины х не­линейным звеном типа «реле» с уровнем насыщения А. Подставляя уравнение реле f(x)=A sign (x) и выражение для нормальной плотности вероятности (1.17)в соотношения (1.27) — (1.28) и учитывая свойства интеграла вероятно­сти (1.21), получаем

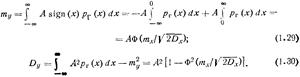
Аналитически решение задачи определения плотности вероятно­сти p(у) нелинейной функции y = f(x) от случайной величины х мо­жет быть получено лишь в том случае, когда существует взаимно однозначное соответствие между х и у, т. е. когда функция f(х) — монотонная.

Пусть f (x) монотонно возрастает. Тогда функция распределения F(y) может быть найдена с помощью соотношения

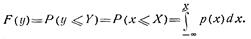
При взаимно однозначном соответствии между х и у из соотноше­ния y=f(x) можно найти обратную функцию 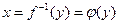поэтому 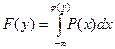. Дифференцирование интеграла по переменной у, входящей в верхний предел, дает

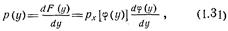
где .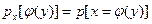

При монотонном убывании f(x)

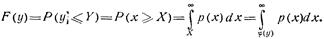
Отсюда

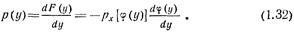
Соотношения (1.31) и (1.32) можно переписать в виде одной фор­мулы:

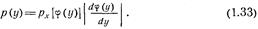
Пример.Пусть 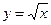, а аргумент х распределен равномерно на интервале [0, 1], т. е.

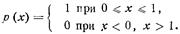
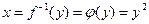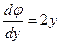Требуется найти p(y). Поскольку в данном , то и

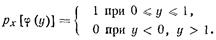
Отсюда

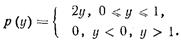
1.1.5. Характеристическая функция и семиинварианты

При решении ряда задач наряду с функцией и плотно­стью распределения вероятностей используют характеристическую функцию случайной величины. Так называют функцию 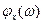, яв­ляющуюся преобразованием Фурье от плотности вероятности:

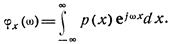
Приведем некоторые свойства характеристических функций

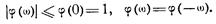
Если 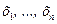— независимые случайные величины и

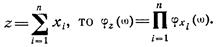
Математическое ожидание и дисперсию случайной величины можно найти, используя производные от логарифма характеристи­ческой функции :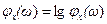

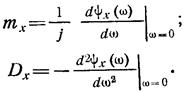
Для гауссовской случайной величины х с математическим ожи­данием т и дисперсией D

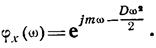
Производную R-го порядка логарифма характеристической функции в точке 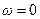, умноженную на 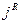, называют семиинвариан­том R-го порядка случайной величины. Первыми двумя семиинвари­антами являются математическое ожидание и дисперсия, а семиин­вариант порядка R есть рациональная функция первых R моментов случайной величины. В частности,

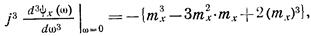
где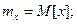

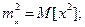
СЛУЧАЙНЫЕ ПРОЦЕССЫ

Спектральная плотность

Наряду с корреляционной функцией для статистического описания стационарных случайных процессов используют спектраль­ную плотность 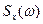. Так называют функцию частоты 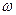, являю­щуюся обратным интегральным преобразованием Фурье от корре­ляционной функции 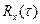случайного процесса x(t):

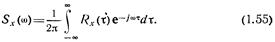
В свою очередь, корреляционная функция процесса x(t) выра­жается через его спектральную плотность как прямое интеграль­ное преобразование Фурье:

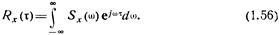
Полагая в (1.56) 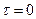, получаем выражение для дисперсии D_x стационарного случайного процесса x(t) через его спектральную плотность:

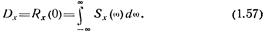
Если в (1.55) и (1.56) перейти к тригонометрической форме представления 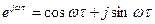и 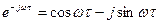, то получим

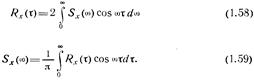
При описании стационарных случайных процессов вместо 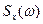может задаваться спектральная плотность, определяемая для поло­жительных частот:

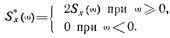
В этом случае корреляционная функция процесса должна вычис­ляться по известной спектральной плотности 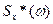с помощью со­отношения

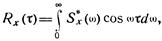
а дисперсия D_x определяется с помощью формулы

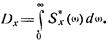
Последнее выражение позволяет дать физическую интерпрета­цию спектральной плотности 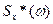: она характеризует плотность распределения дисперсии стационарного случайного процесса по частотам непрерывного спектра гармонического разложения этого процесса.

Рассмотрим два примера определения спектральных плотностей стационарных случайных процессов по их корреляционным функ­циям.

Белый шум.Для белого шума 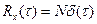, поэтому из (1.59) находим, учитывая свойство 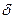-функции,

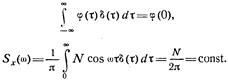
Как видим, спектральная плотность белого шума остается по­стоянной на бесконечном интервале частот. Это указывает на физи­ческую нереализуемость такого шума, поскольку для его реализа­ции потребовалась бы бесконечно большая энергия источника тако­го шума. Равномерное распределение дисперсии на бесконечном интервале частот может также использоваться в качестве иного определения белого шума. Спектр солнечного света в оптическом диапазоне близок к равномерному. Учитывая эту аналогию, случай­ный процесс с равномерной спектральной плотностью называют бе­лым шумом. Все другие случайные процессы, у которых функция .S'_x(co) меняется по частоте, можно называть «окрашенными» шума­ми. На практике в качестве белого рассматривают любой окрашен­ный шум, спектральная плотность которого остается постоянной в пределах полосы пропускания системы, на которую этот шум дей­ствует.

Экспоненциально коррелированный процесс.Случайный про­цесс с корреляционной функцией вида

называют экспоненциально корреляционным. Спектральную плот-кость такого процесса можно найти с помощью формулы (1.55)

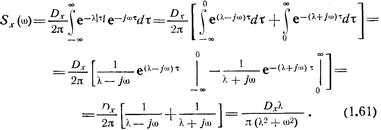
СЛУЧАЙНЫЕ ПОЛЯ

При исследовании управляемого движения летательных аппаратов некоторые факторы, как, например, плотность, темпера­тура, турбулентность в реальной (не стандартной) атмосфере, изме­няются случайно в зависимости от координат рассматриваемой точ­ки пространства и времени t.

Случайные факторы, аргументами которых являются векторы, называют случайными полями.

Если в состав компонент вектора аргументов поля входят только координаты пространства, то такое случайное поле называют про­странственным. Если же в состав аргументов поля входит также и время, то случайное поле называют пространственно-временным.

Случайные поля бывают скалярными и векторными. Плотность воздуха в атмосфере р(х, у, z, t) и его температура Т(х, у, z, t) — скалярные пространственно-временные случайные поля. Турбулент­ность атмосферы w(x, у, z, t) есть векторное пространственно-вре­менное случайное поле, поскольку скорость порывов ветра в турбу­лентной атмосфере да— это вектор, характеризуемый тремя состав­ляющими w_x, w_v, w_z.

Скалярные случайные поля

Обозначим вектором х= {х, у, z} вектор аргументов про­странственного скалярного случайного поля и(х). Вектор х опреде­лен в области D возможного изменения координат х, у, z. Точку 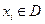назовем точкой наблюдения поля. В каждой точке скаляр­ного поля наблюдается скалярная случайная величина .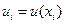

Скалярное случайное поле и(х) считается описанным полностью, если для произвольного числа точек наблюдения 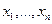известен способ построения «-мерного совместного безусловного распреде­ления вероятностей 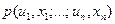системы случайных величин .

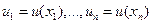В частности, если при любых 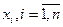, и любом п справедливо соотношение

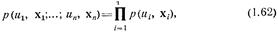
то поле и(х) называется абсолютно случайным, и для его описания достаточно задать зависимость одномерной плотности р_u(х) от ко­ординат х точки наблюдения этого поля.

Как и при описании случайных величин и процессов, для описа­ния случайных полей часто пользуются их моментными характерис­тиками.

n-точечным начальным моментом порядка t_i + ... + i_n скалярно­го поля и(х) называется математическое ожидание произведения соответствующих степеней возможных значений поля в n точках наблюдения:

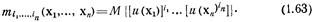
Одноточечный начальный момент первого порядка

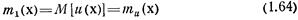
называется математическим ожиданием скалярного случайного поля. Оно характеризует среднее значение случайной величины и в каждой точке х области D.

Разность 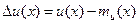есть центрированное случайное поле. Среднюю величину произведения степеней 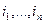возмож­ных значений центрированного поля 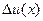в n точках наблюдения называют «-точечным центральным моментом порядка :

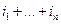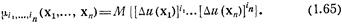
Одноточечный центральный момент второго порядка

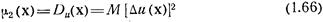
есть дисперсия скалярного поля u(х), а двухточечный центральный момент второго порядка

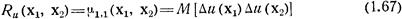
— его корреляционная функция. Дисперсия случайного поля харак­теризует рассеивание случайных значений поля в точке наблюде­ния, а корреляционная функция — корреляцию значений поля в двух его точках наблюдения х₁ и х₂.

Скалярное случайное поле может обладать свойствами однород­ности и изотропности. Поле и(х) называется однородным (строгая однородность), если его n -точечное совместное распределение не изменяется при переносе точек наблюдения этого поля 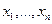на один и тот же вектор х₀, т. е.

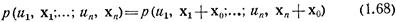
при любом х₀ и любом числе точек наблюдения п.

Скалярное случайное поле u(х) называется однородным в широ­ком смысле, если его математическое ожидание т_u(х) является постоянным во всех точках области D, а корреляционная функция 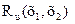не изменяется при переносе пары точек наблюдения х₁ и х₂ на один и тот же вектор х₀, т. е.

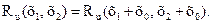(1.69)

Иными словами, аргументом корреляционной функции однородно­го скалярного поля являются не координаты х₁ и х₂ точек наблю­дения этого поля, а вектор 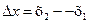соединяющий эти точки в области D. Свойство однородности скалярного случайного поля эквивалентно свойству стационарности случайного процесса.

Однородное скалярное поле u(х) называется изотропным, если корреляция между значениями этого поля в точках х₁ и х₂ не зави­сит от ориентации вектора 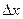, а зависит только от его длины 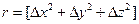. Таким образом, в рамках корреляционной теории изотропное скалярное случайное поле u(х) описывается двумя ха­рактеристиками: математическим ожиданием m_u(x)=const и кор­реляционной функцией R_u(r).

Векторные случайные поля

Рассмотрим векторное пространственное случайное по­ле и(х), у которого аргумент х - вектор с координатами х, у, z, принадлежащий области наблюдения поля D, а и — вектор с проек­циями и_х, и_у, u_z.

Проекции и_х(х), и_у(х), u_z(x) можно рассматривать как совокуп­ность трех случайных полей. Статистическое описание этой совокуп­ности эквивалентно статистическому описанию векторного поля и(х). В рамках корреляционной теории для описания совокупности скалярных случайных полей и_х(х), и_у(х) и u_z(x) требуется задать вектор их математических ожиданий т_и(х) и матричную корреля­ционную функцию 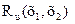. Вектор математических ожиданий со­стоит из трех компонент 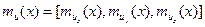, каждая из которых есть математическое ожидание соответствующей со­ставляющей вектора и в точке наблюдения х.

Матричная корреляционная функция 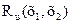характеризует статистическую взаимосвязь между различными компонентами век­тора и в двух различных точках наблюдения поля х₁ и х₂ в облас­ти D:

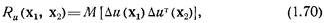
где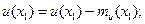

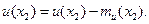
Если поле ы(х), у которого аргумент х состоит из трех компо­нент х, у, z, содержит три компоненты и_х, и_у, и_z, то матричная кор­реляционная функция 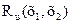имеет размерность 3×3. Элементы 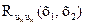, 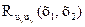и 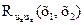— автокорреляционные функции составляющих и_х, и_у и и_z векторного поля; остальные эле­менты— взаимные корреляционные функции между различными составляющими этого поля. Например, корреляция между компо-

нентами и_х и и_у в точках наблюдения х₁ и х₂ характеризуется вза­имной корреляционной функцией

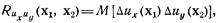
где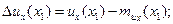

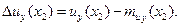
При х₁-х₂=х, т. е. при совпадении двух точек наблюдения, матричная корреляционная функция 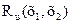векторного случай­ного поля u(х) обращается в его корреляционную матрицу K_u(x), диагональными элементами которой являются дисперсии составля­ющих и_х, и_у, u_z вектора и в точке х, а внедиагональными — взаим­ные корреляционные моменты этих составляющих.

Как и скалярное, векторное случайное поле может быть одно­родным и изотропным. Статистические характеристики однородно­го векторного случайного поля u(х) инвариантны относительно па­раллельного переноса точек наблюдения поля в области D на оди­наковый вектор х₀ произвольной длины. Для такого поля математи­ческое ожидание есть постоянный вектор 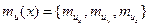, a матричная корреляционная функция 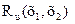зависит только от вектора 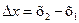соединяющего точки наблюдения х₁ и х₂, и не зависит от положения точки х₁ начала вектора 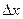в области D.

Для рассмотрения свойства и