Материалы для практических занятий по оценке выполнения заданий
С развернутым ответом
Задание 21.
Пример 1.
Решите уравнение 
.
Ответ: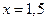 
, 
.
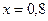Комментарий.
При нахождении корней квадратного уравнения допущена неверная запись. При наличии общей формулы для нахождения корней квадратного уравнения, записанной верно, не извлечен корень из дискриминанта, все дальнейшие вычисления (с этой ошибкой) выполнены верно. Вычислительная ошибка присутствует, с её учётом дальнейшие шаги выполнены верно.
Оценка эксперта: 1 балл.
Пример 2.
Решите уравнение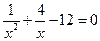 
.
Ответ: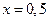 
, 
.
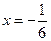Комментарий.
Правильно выполнены преобразования, получен верный ответ.
Оценка эксперта: 2 балла.
Пример 3.
Решите уравнение .
Ответ: , .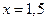
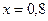Комментарий.
Все этапы решения присутствуют, корни в правом столбце найдены верно. Неверную запись ответа можно рассмотреть как описку.
Оценка эксперта: 1 балл.
Пример 4.
Решите уравнение .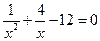
Ответ: , .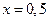
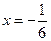Комментарий.
Все этапы решения присутствуют, корни найдены верно. Неверную запись ответа можно рассмотреть как неверное владение символикой (хочется надеяться, что учащийся хотел написать фигурные скобки).
Оценка эксперта: 1 балл.
Задание 22.
Пример 1.
Игорь и Паша могут покрасить забор за 20 часов, Паша и Володя – за 21 час, а Володя и Игорь за 28 часов. За какое время покрасят забор мальчики, работая втроем. Ответ дайте в минутах.
Ответ: 900 минут.
Комментарий.
Ход решения верный, ответ верный.
Оценка эксперта: 2 балла.
Пример 2.
Игорь и Паша могут покрасить забор за 14 часов, Паша и Володя – за 15 часов, а Володя и Игорь за 30 часов. За какое время покрасят забор мальчики, работая втроем. Ответ дайте в минутах.
Ответ: 700 минут.
Комментарий.
Логическая ошибка – выпускник перепутал производительность и время.
Оценка эксперта: 0 баллов.
Пример 3.
Игорь и Паша могут покрасить забор за 14 часов, Паша и Володя – за 15 часов, а Володя и Игорь за 30 часов. За какое время покрасят забор мальчики, работая втроем. Ответ дайте в минутах.
Ответ: 700 минут.
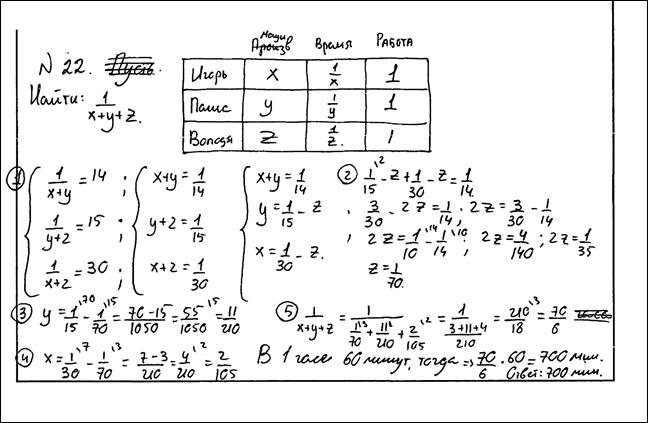
Комментарий.
Ход решения верный, ответ верный.
Оценка эксперта: 2 балла.
Пример 4.
Игорь и Паша могут покрасить забор за 14 часов, Паша и Володя – за 15 часов, а Володя и Игорь за 30 часов. За какое время покрасят забор мальчики, работая втроем. Ответ дайте в минутах.
Ответ: 700 минут.
Комментарий.
Арифметическая ошибка на последнем шаге.
Оценка эксперта: 1 балл.
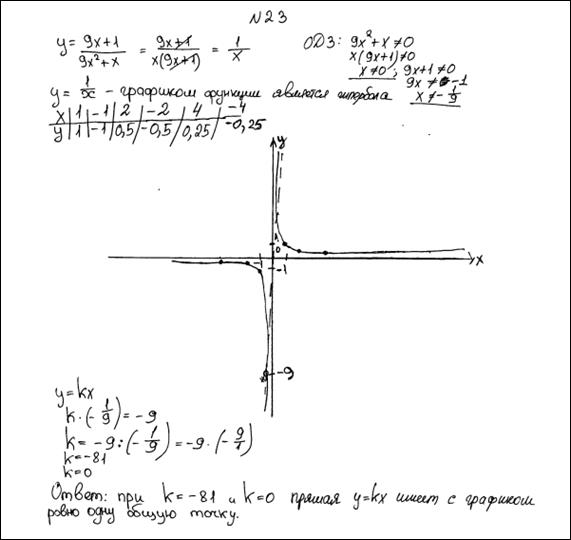
Задание 23.
Пример 1.
Постройте график функции 
и определите, при каких значениях k прямая 
имеет с графиком ровно одну общую точку.
Ответ: 0,49.
Комментарий.
Форма графика соблюдена, выколотая точка обозначена верно. Вторая часть задания не выполнена.
Оценка эксперта: 1 балл.
Пример 2.
Постройте график функции 
и определите, при каких значениях k прямая имеет с графиком ровно одну общую точку.
Ответ: 81.
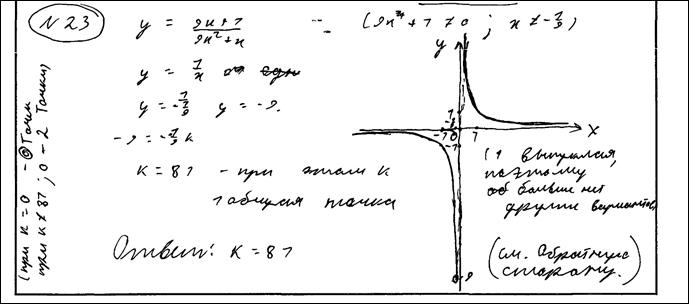
Комментарий.
Форма графика соблюдена, выколотая точка обозначена верно. Вторая часть задания выполнена верно.
Оценка эксперта: 2 балла.
Пример 3.
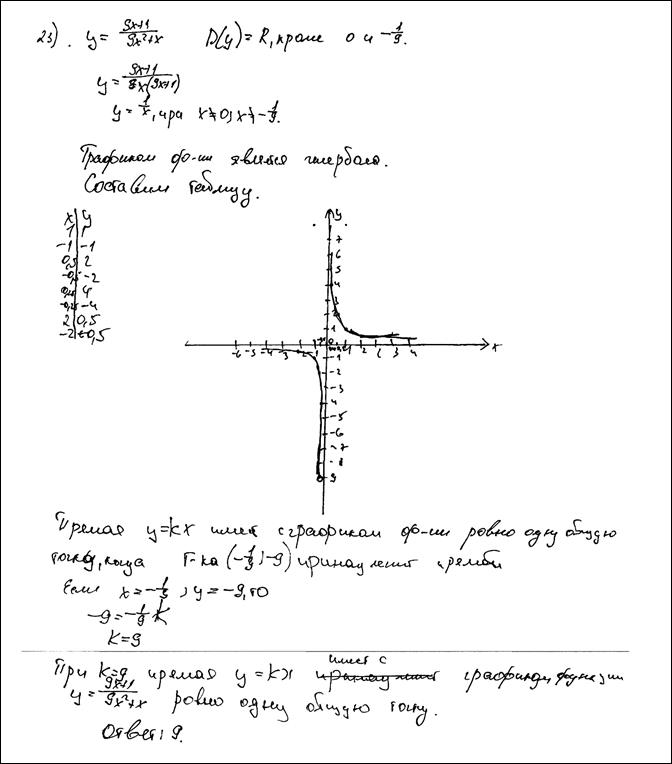
Постройте график функции и определите, при каких значениях k прямая имеет с графиком ровно одну общую точку.
Ответ: 81.
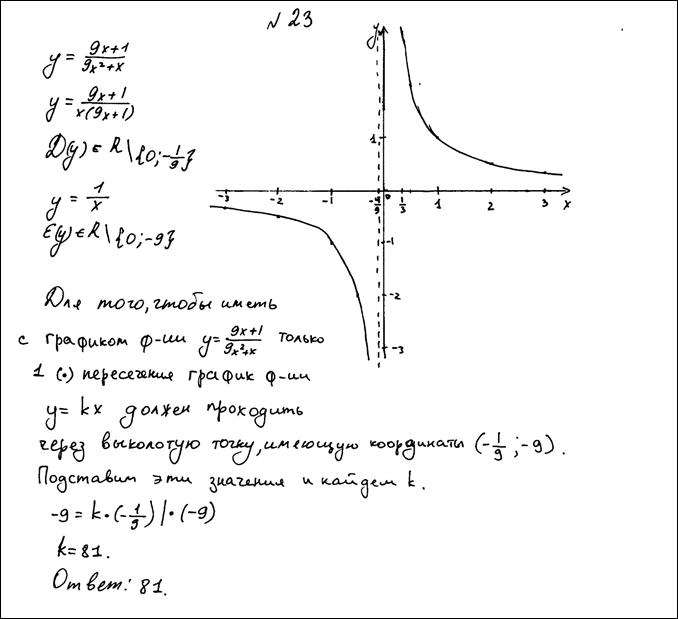
Комментарий.
Несмотря на описание, по данному рисунку нельзя судить о верности графика.
Оценка эксперта: 0 баллов.
Пример 4.
Постройте график функции и определите, при каких значениях k прямая имеет с графиком ровно одну общую точку.
Ответ: 81.
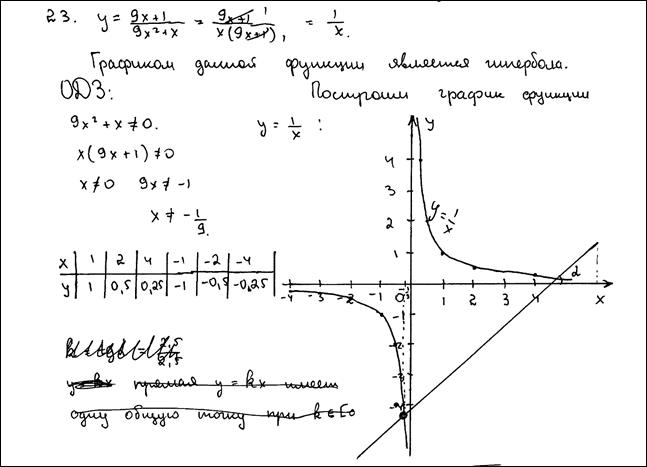
Комментарий.
График построен верно. Наличие некоторой прямой на графике не может быть поводом для снижения баллов.
Оценка эксперта: 1 балл.
Задание 24.
Пример 1.
Высота, опущенная из вершины ромба, делит противоположную сторону на отрезки равные 24 и 2, считая от вершины острого угла. Вычислите длину высоты ромба.
Ответ: 10.
Комментарий.
Арифметическая ошибка под знаком корня.
Оценка эксперта: 1балл.
Пример 2.
Высота, опущенная из вершины ромба, делит противоположную сторону на отрезки равные 24 и 2, считая от вершины острого угла. Вычислите длину высоты ромба.
Ответ: 10.
Комментарий.
Учащийся решает свою задачу: не учтен порядок расположения отрезков.
Оценка эксперта: 0баллов.
Пример 3.
Высота, опущенная из вершины ромба, делит противоположную сторону на отрезки равные 24 и 2, считая от вершины острого угла. Вычислите длину высоты ромба.
Ответ: 10.
Комментарий.
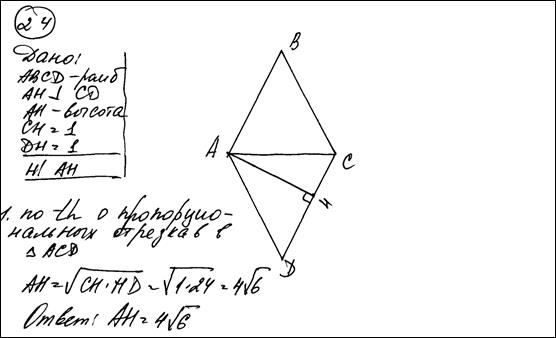
Задача выполнена верно, не смотря на изображение перпендикуляра AH.
Оценка эксперта: 2балла.
4.5. Задание 25.
Пример 1.
Две окружности с центрами E и F пересекаются в точках C и D, центры E и F лежат по одну сторону относительно прямой CD. Докажите, что прямая CD перпендикулярна прямой EF.
Комментарий.
Неточность в обосновании (см. пункт 5)
Оценка эксперта: 1балл.
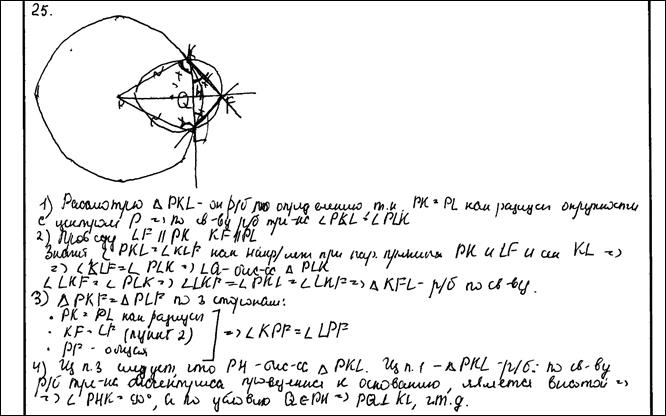
Пример 2.
Две окружности с центрами E и F пересекаются в точках C и D, центры E и F лежат по одну сторону относительно прямой CD. Докажите, что прямая CD перпендикулярна прямой EF.
Комментарий.
Не доказано, почему FH делит CD пополам.
Оценка эксперта: 0баллов.
Пример 3.
Две окружности с центрами E и F пересекаются в точках C и D, центры E и F лежат по одну сторону относительно прямой CD. Докажите, что прямая CD перпендикулярна прямой EF.
Комментарий.
Классическое доказательство данного факта.
Оценка эксперта: 2баллов.
Задание 26.
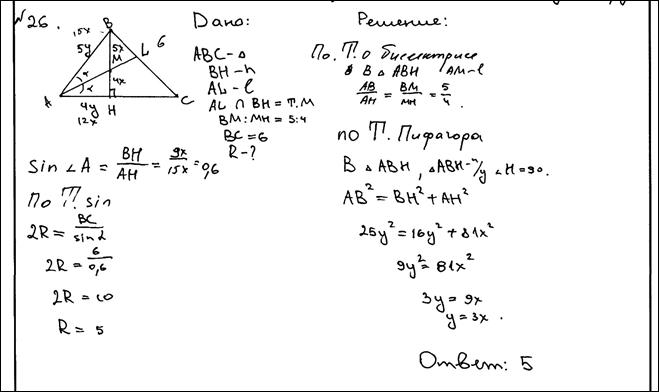
Пример 1.
Биссектриса угла A, треугольника ABC делит высоту BH в отношении 5:4, считая от вершины. BC равно 6. Найдите радиус описанной окружности.
Ответ: 5.
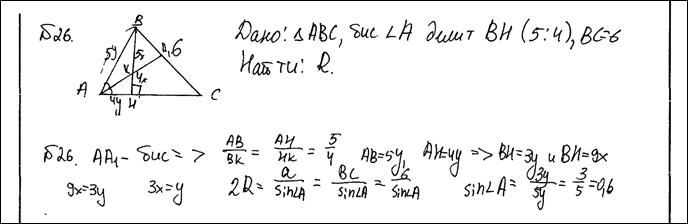
Комментарий.
Решение незаконченное: формула для нахождения радиуса выписана, все компоненты найдены, но не получен итоговый результат.
Оценка эксперта: 1балл.
Пример 2.
Биссектриса A, треугольника ABC делит высоту BH в отношении 25:24, считая от вершины. BC равно 14. Найдите радиус описанной окружности.
Ответ: 25.
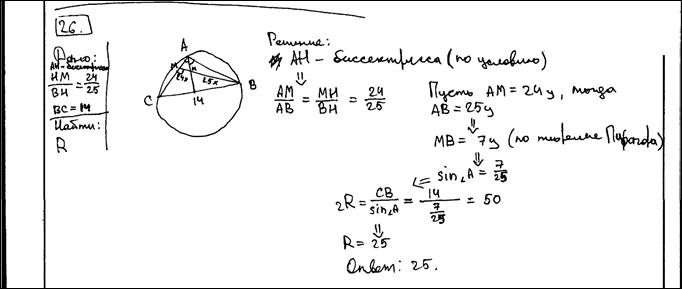
Комментарий.
Решение верное.
Оценка эксперта: 2балла.
Пример 3.
Биссектриса угла A, треугольника ABC делит высоту BH в отношении 5:4, считая от вершины. BC равно 6. Найдите радиус описанной окружности.
Ответ: 5.
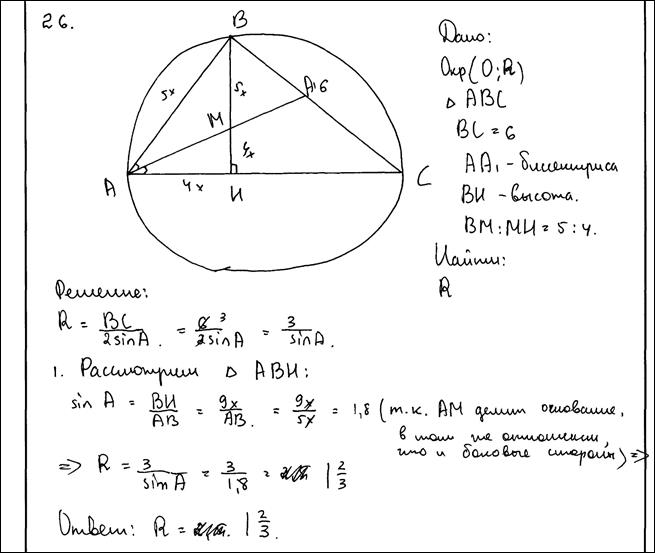
Комментарий.
Логическая ошибка, неверно применено свойство биссектрисы.
Оценка эксперта: 0баллов.
Пример 4.
Биссектриса A, треугольника ABC делит высоту BH в отношении 25:24, считая от вершины. BC равно 14. Найдите радиус описанной окружности.
Ответ: 25.
Комментарий.
Арифметическая ошибка.
Оценка эксперта: 1балл.
Рекомендуется следующий порядок самостоятельной работы эксперта:
а) прочесть все 6 решений подряд и составить свое предварительное мнение об оценках;
б) вернуться к началу и прочесть все решения еще раз, на этот раз выставляя свои собственные оценки, в соответствии с критериями оценивания;
в) после этого сверить свои оценки с предлагаемыми оценками в таблице ответов;
г) при наличии расхождений в оценках вернуться к спорным моментам и обсудить их или с проводящим семинар по подготовке экспертов, или с руководителем региональной экспертной группы, или с консультантом федеральной предметной группы.
В каждой части приложена таблица ответов.
Задание 21 с развернутым ответом повышенного уровня сложности. Задание для самостоятельной работы экспертов.
Задание 1.Решите уравнение .
Ответ: 
, .
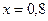Оценка эксперта: ____________________
Задание 2.Решите уравнение .
Ответ: , .
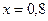Оценка эксперта: ____________________
Задание 3.
Решите уравнение .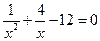
Ответ: 
, .
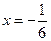Оценка эксперта: ____________________
Задание 4.
Решите уравнение .
Ответ: , .
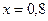Оценка эксперта: ____________________
Задание 21.
| Задание | ||||
| Оценка эксперта |
Задание 22 с развернутым ответом повышенного уровня сложности. Задание для самостоятельной работы экспертов.
Задание 1.
Игорь и Паша могут покрасить забор за 20 часов, Паша и Володя – за 21 час, а Володя и Игорь за 28 часов. За какое время покрасят забор мальчики, работая втроем. Ответ дайте в минутах. Ответ: 900 минут.
Оценка эксперта: ____________________
Задание 2.
Игорь и Паша могут покрасить забор за 20 часов, Паша и Володя – за 21 час, а Володя и Игорь за 28 часов. За какое время покрасят забор мальчики, работая втроем. Ответ дайте в минутах. Ответ: 900 минут.
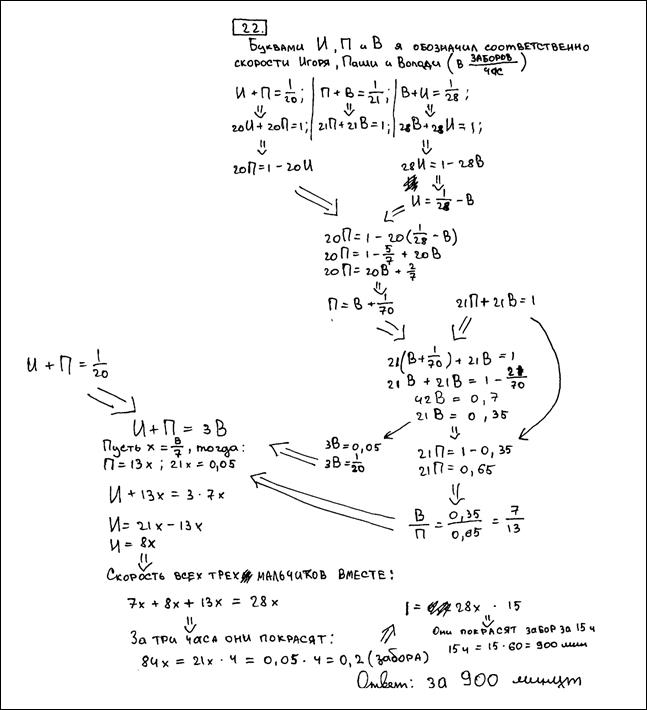
Оценка эксперта: ____________________
Задание 3.
Игорь и Паша могут покрасить забор за 14 часов, Паша и Володя – за 15 часов, а Володя и Игорь за 30 часов. За какое время покрасят забор мальчики, работая втроем. Ответ дайте в минутах. Ответ: 700 минут.
Оценка эксперта: ____________________
Задание 4.
Игорь и Паша могут покрасить забор за 20 часов, Паша и Володя – за 21 час, а Володя и Игорь за 28 часов. За какое время покрасят забор мальчики, работая втроем. Ответ дайте в минутах. Ответ: 900 минут.
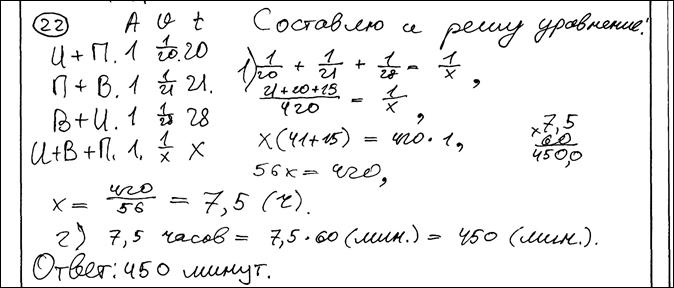
Оценка эксперта: ____________________
Задание 5.
Игорь и Паша могут покрасить забор за 20 часов, Паша и Володя – за 21 час, а Володя и Игорь за 28 часов. За какое время покрасят забор мальчики, работая втроем. Ответ дайте в минутах. Ответ: 900 минут.
Оценка эксперта: ____________________
Задание 22.
| Задание | |||||
| Оценка эксперта |
Задание 23 с развернутым ответом повышенного уровня сложности. Задание для самостоятельной работы экспертов.
Задание 1.
Постройте график функции: и определите, при каких значениях k прямая имеет с графиком ровно одну общую точку. Ответ: 0,49.
Оценка эксперта: ____________________
Задание 2.
Постройте график функции: и определите, при каких значениях k прямая имеет с графиком ровно одну общую точку. Ответ: 0,49.
Оценка эксперта: ____________________
Задание 3.
Постройте график функции: и определите, при каких значениях k прямая имеет с графиком ровно одну общую точку. Ответ: 81.
Оценка эксперта: ____________________
Задание 4.
Постройте график функции: и определите, при каких значениях k прямая имеет с графиком ровно одну общую точку. Ответ: 0,49.
Оценка эксперта: ____________________
Задание 5.
Постройте график функции: и определите, при каких значениях k прямая имеет с графиком ровно одну общую точку. Ответ: 81.
Оценка эксперта: ____________________
Задание 23.
| Задание | |||||
| Оценка эксперта |
Задание 24 с развернутым ответом повышенного уровня сложности. Задание для самостоятельной работы экспертов.
Задание 1.
Высота, опущенная из вершины ромба, делит противоположную сторону на отрезки равные 24 и 2, считая от вершины острого угла. Вычислите длину высоты ромба.
Ответ: 10.
Оценка эксперта: ____________________
Задание 2.
Высота, опущенная из вершины ромба, делит противоположную сторону на отрезки равные 24 и 2, считая от вершины острого угла. Вычислите длину высоты ромба.
Ответ: 10.
Оценка эксперта: ____________________
Задание 3.
Высота, опущенная из вершины ромба, делит противоположную сторону на отрезки равные 24 и 2, считая от вершины острого угла. Вычислите длину высоты ромба.
Ответ: 10.
Оценка эксперта: ____________________
Задание 4.
Высота, опущенная из вершины ромба, делит противоположную сторону на отрезки равные 24 и 2, считая от вершины острого угла. Вычислите длину высоты ромба.
Ответ: 10.
Оценка эксперта: ____________________
Задание 24.
| Задание | ||||
| Оценка эксперта |
Задание 25 с развернутым ответом повышенного уровня сложности. Задание для самостоятельной работы экспертов.
Задание 1.
Две окружности с центрами E и F пересекаются в точках C и D, центры E и F лежат по одну сторону относительно прямой CD. Докажите, что прямая CD перпендикулярна прямой EF.
Оценка эксперта: ____________________
Задание 2.
Две окружности с центрами E и F пересекаются в точках C и D, центры E и F лежат по одну сторону относительно прямой CD. Докажите, что прямая CD перпендикулярна прямой EF.
Оценка эксперта: ____________________
Задание 3.
Две окружности с центрами E и F пересекаются в точках C и D, центры E и F лежат по одну сторону относительно прямой CD. Докажите, что прямая CD перпендикулярна прямой EF.
Оценка эксперта: ____________________
Задание 4.
Две окружности с центрами E и F пересекаются в точках C и D, центры E и F лежат по одну сторону относительно прямой CD. Докажите, что прямая CD перпендикулярна прямой EF.
Оценка эксперта: ____________________
Задание 25.
| Задание | ||||
| Оценка эксперта |
Задание 26 с развернутым ответом высокого уровня сложности.
Задание для самостоятельной работы экспертов.
Задание 1.
Биссектриса угла A, треугольника ABC делит высоту BH в отношении 5:4, считая от вершины. BC равно 6. Найдите радиус описанной окружности. Ответ: 5.
Оценка эксперта: ____________________
Задание 2.
Биссектриса угла A, треугольника ABC делит высоту BH в отношении 5:4, считая от вершины. BC равно 6. Найдите радиус описанной окружности. Ответ: 5.
Оценка эксперта: ____________________
Задание 3.
Биссектриса угла A, треугольника ABC делит высоту BH в отношении 5:4, считая от вершины. BC равно 6. Найдите радиус описанной окружности. Ответ: 5.
Оценка эксперта: ____________________
Задание 4.
Биссектриса A, треугольника ABC делит высоту BH в отношении 25:24, считая от вершины. BC равно 14. Найдите радиус описанной окружности. Ответ: 25.
Оценка эксперта: ____________________
Задание 26.
| Задание | ||||
| Оценка эксперта |
§5. Тренировочные варианты.
Вариант 1.
№1.Решите уравнение 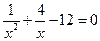.Ответ: 
, .
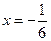| Баллы | Критерии оценки выполнения задания |
| Правильно выполнены преобразования, получен верный ответ | |
| Решение доведено до конца, но допущена ошибка вычислительного характера или описка, с её учётом дальнейшие шаги выполнены верно | |
| Другие случаи, не соответствующие указанным критериям | |
| Максимальный балл |
Оценка эксперта:___________________________________________________
Комментарий:_____________________________________________________
№2.Решите уравнение . Ответ: , 
.
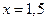Оценка эксперта:______________________________________________________
Комментарий:___________________________________________________________________________________________________________________________________
№3.Решите уравнение . Ответ: , .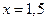
Оценка эксперта:________________________________________________________
Комментарий:___________________________________________________________________________________________________________________________________
№4. Игорь и Паша могут покрасить забор за 20 часов, Паша и Володя – за 21 час, а Володя и Игорь за 28 часов. За какое время покрасят забор мальчики, работая втроем. Ответ дайте в минутах. Ответ: 900 минут.
| Баллы | Критерии оценки выполнения задания |
| Правильно составлено уравнение, получен верный ответ | |
| Правильно составлено уравнение, но при его решении допущена вычислительная ошибка, с её учётом решение доведено до ответа | |
| Другие случаи, не соответствующие указанным критериям | |
| Максимальный балл |
Оценка эксперта:___________________________________________________
Комментарий:_______________________________________________________________________________________________________________________
№5. Игорь и Паша могут покрасить забор за 14 часов, Паша и Володя – за 15 часов, а Володя и Игорь за 30 часов. За какое время покрасят забор мальчики, работая втроем. Ответ дайте в минутах. Ответ: 700 минут.
. 
Оценка эксперта:_______________________________________________________
Комментарий:___________________________________________________________________________________________________________________________________
№6. Игорь и Паша могут покрасить забор за 20 часов, Паша и Володя – за 21 час, а Володя и Игорь за 28 часов. За какое время покрасят забор мальчики, работая втроем. Ответ дайте в минутах. Ответ: 900 минут.
Оценка эксперта:________________________________________________________
Комментарий:___________________________________________________________________________________________________________________________________
№7. Постройте график функции: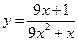 
и определите, при каких значениях k прямая 
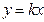имеет с графиком ровно одну общую точку. Ответ: 81.
| Баллы | Критерии оценки выполнения задания |
| График построен правильно, верно указаны все значения c , при которых прямая y = c имеет с графиком только одну общую точку | |
| График построен правильно, указаны не все верные значения c | |
| Другие случаи, не соответствующие указанным критериям | |
| Максимальный балл |
Оценка эксперта:________________________________________________________
Комментарий:___________________________________________________________________________________________________________________________________
№8. Постройте график функции: 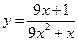и определите, при каких значениях k прямая 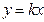имеет с графиком ровно одну общую точку. Ответ: 81.
Оценка эксперта:________________________________________________________
Комментарий:___________________________________________________________________________________________________________________________________
№9. Высота, опущенная из вершины ромба, делит противоположную сторону на отрезки равные 24 и 2, считая от вершины острого угла. Вычислите длину высоты ромба. Ответ: 10.
| Баллы | Критерии оценки выполнения задания |
| Получен верный обоснованный ответ | |
| При верных рассуждениях допущена вычислительная ошибка, возможно приведшая к неверному ответу | |
| Другие случаи, не соответствующие указанным критериям | |
| Максимальный балл |
Оценка эксперта:___________________________________________________ Комментарий:_______________________________________________________________________________________________________________________
№10. Высота, опущенная из вершины ромба, делит противоположную сторону пополам, на отрезки равные 1. Вычислите длину высоты ромба. Ответ: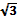 
.
Оценка эксперта:___________________________________________________ Комментарий:_____________________________________________________
№11. Высота, опущенная из вершины ромба, делит противоположную сторону на отрезки равные 24 и 2, считая от вершины острого угла. Вычислите длину высоты ромба. Ответ: 10.
Оценка эксперта:___________________________________________________ Комментарий:_____________________________________________________
№12.Две окружности с центрами E и F пересекаются в точках C и D, центры E и F лежат по одну сторону относительно прямой CD. Докажите, что прямая CD перпендикулярна прямой EF.
| Баллы | Критерии оценки выполнения задания |
| Доказательство верное, все шаги обоснованы | |
| Доказательство в целом верное, но содержит неточности | |
| Другие случаи, не соответствующие указанным критериям | |
| Максимальный балл |
Оценка эксперта:___________________________________________________ Комментарий:_____________________________________________________
___________________________________________________________________
№13.Две окружности с центрами P и Q пересекаются в точках K и L, центры P и Q лежат по одну сторону относительно прямой KL. Докажите, что прямая PQ перпендикулярна прямой KL.
Оценка эксперта:___________________________________________________ Комментарий:_____________________________________________________
___________________________________________________________________
№14. Биссектриса угла A, треугольника ABC делит высоту BH в отношении 5:4, считая от вершины. Длина BC равна 6. Найдите радиус описанной окружности.
Ответ: 5.
| Баллы | Критерии оценки выполнения задания |
| Ход решения верный, все его шаги выполнены правильно, получен верный ответ | |
| Ход решения верный, чертёж соответствует условию задачи, но пропущены существенные объяснения или допущена вычислительная ошибка | |
| Другие случаи, не соответствующие указанным критериям | |
| Максимальный балл |
Оценка эксперта:___________________________________________________ Комментарий:_____________________________________________________
№15. Биссектриса A, треугольника ABC делит высоту BH в отношении 25:24, считая от вершины. Длина BC равна 14. Найдите радиус описанной окружности.
Ответ: 25.
Оценка эксперта:___________________________________________________ Комментарий:_____________________________________________________
___________________________________________________________________
Вариант 2
№1.Решите уравнение . Ответ: , .
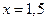| Баллы | Критерии оценки выполнения задания |
| Правильно выполнены преобразования, получен верный ответ | |
| Решение доведено до конца, но допущена ошибка вычислительного характера или описка, с её учётом дальнейшие шаги выполнены верно | |
| Другие случаи, не соответствующие указанным критериям | |
| Максимальный балл |
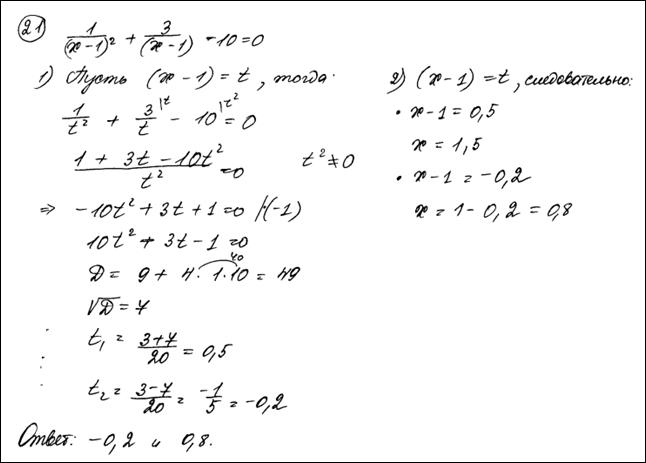
Оценка эксперта:___________________________________________________
Комментарий:_____________________________________________________
__________________________________________________________________
№2.Решите уравнение 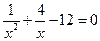. Ответ: , .
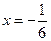Оценка эксперта:___________________________________________________
Комментарий:_____________________________________________________
№3.Решите уравнение . Ответ: , .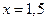
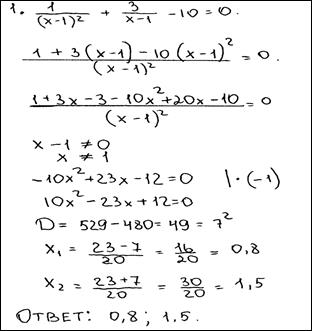
Оценка эксперта:___________________________________________________
Комментарий:_____________________________________________________
№4.Игорь и Паша могут покрасить забор за 20 часов, Паша и Володя – за 21 час, а Володя и Игорь за 28 часов. За какое время покрасят забор мальчики, работая втроем. Ответ дайте в минутах. Ответ: 900 минут.
| Баллы | Критерии оценки выполнения задания |
| Правильно составлено уравнение, получен верный ответ | |
| Правильно составлено уравнение, но при его решении допущена вычислительная ошибка, с её учётом решение доведено до ответа | |
| Другие случаи, не соответствующие указанным критериям | |
| Максимальный балл |
Начало решения задания №4
Продолжение на следующей странице
Продолжение решения задания №4
Оценка эксперта:___________________________________________________
Комментарий:_____________________________________________________
__________________________________________________________________
№5.Игорь и Паша могут покрасить забор за 20 часов, Паша и Володя – за 21 час, а Володя и Игорь за 28 часов. За какое время покрасят забор мальчики, работая втроем. Ответ дайте в минутах. Ответ: 900 минут.
Оценка эксперта:___________________________________________________
Комментарий:_____________________________________________________
№6.Игорь и Паша могут покрасить забор за 14 часов, Паша и Володя – за 15 часов, а Володя и Игорь за 30 часов. За какое время покрасят забор мальчики, работая втроем. Ответ дайте в минутах. . Ответ: 700 минут.
Оценка эксперта:___________________________________________________
Комментарий:_____________________________________________________
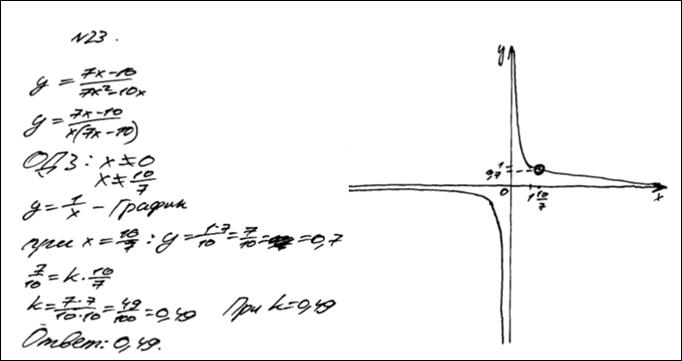
№7.Постройте график функции: и определите, при каких значениях k прямая 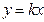имеет с графиком ровно одну общую точку. Ответ: 0,49.
| Баллы | Критерии оценки выполнения задания |
| График построен правильно, верно указаны все значения c , при которых прямая y = c имеет с графиком только одну общую точку | |
| График построен правильно, указаны не все верные значения c | |
| Другие случаи, не соответствующие указанным критериям | |
| Максимальный балл |
Оценка эксперта:___________________________________________________
Комментарий:_____________________________________________________
__________________________________________________________________
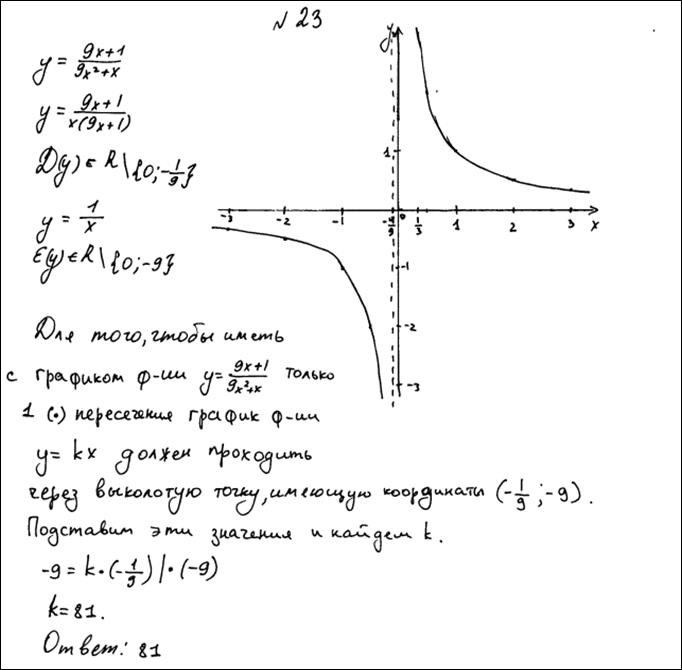
№8.Постройте график функции: 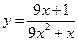и определите, при каких значениях k прямая 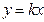имеет с графиком ровно одну общую точку. Ответ: 81.
Оценка эксперта:___________________________________________________
Комментарий:_____________________________________________________
__________________________________________________________________
№9.Высота, опущенная из вершины ромба, делит противоположную сторону на отрезки равные 24 и 2, считая от вершины острого угла. Вычислите длину высоты ромба. Ответ: 10.
| Баллы | Критерии оценки выполнения задания |
| Получен верный обоснованный ответ | |
| При верных рассуждениях допущена вычислительная ошибка, возможно приведшая к неверному ответу | |
| Другие случаи, не соответствующие указанным критериям | |
| Максимальный балл |
Оценка эксперта:___________________________________________________
Комментарий:_____________________________________________________
__________________________________________________________________
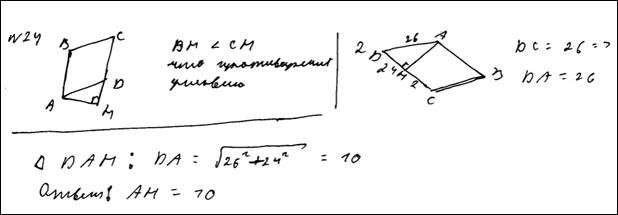
№10. Высота, опущенная из вершины ромба, делит противоположную сторону на отрезки равные 24 и 2, считая от вершины острого угла. Вычислите длину высоты ромба. Ответ: 10.
Оценка эксперта:___________________________________________________
Комментарий:_____________________________________________________
__________________________________________________________________
№11.Высота, опущенная из вершины ромба, делит противоположную сторону на отрезки равные 24 и 2, считая от вершины острого угла. Вычислите длину высоты ромба. Ответ: 10.
Оценка эксперта:___________________________________________________
Комментарий:_____________________________________________________
__________________________________________________________________
№12.Две окружности с центрами E и F пересекаются в точках C и D, центры E и F лежат по одну сторону относительно прямой CD. Докажите, что прямая CD перпендикулярна прямой EF.
| Баллы | Критерии оценки выполнения задания |
| Доказательство верное, все шаги обоснованы | |
| Доказательство в целом верное |