Общие подходы к проверке и оценке выполнения заданий

С развернутым ответом

Требования к выполнению заданий с развернутым ответом заключаются в следующем: решение должно быть математически грамотным и полным, из него должен быть понятен ход рассуждений учащегося. Оформление решения должно обеспечивать выполнение указанных выше требований, а в остальном может быть произвольным. Не следует требовать от учащихся слишком подробных комментариев (например, описания алгоритмов). Лаконичное решение, не содержащее неверных утверждений, все выкладки которого правильны, следует рассматривать как решение без недочетов.

Если решение заданий 21–26 удовлетворяет этим требованиям, то выставляется полный балл – 2 балла за каждое задание. Если в решении допущена ошибка непринципиального характера (вычислительная, погрешность в терминологии или символике и др.), не влияющая на правильность общего хода решения (даже при неверном ответе) и позволяющая, несмотря на ее наличие, сделать вывод о владении материалом, то учащемуся засчитывается балл, на 1 меньший указанного, что и отражено в критериях оценивания заданий с развернутым ответом.

В критериях оценивания по каждому конкретному заданию второй части экзаменационной работы эти общие позиции конкретизируются и пополняются с учетом содержания задания. Критерии разработаны применительно к одному из возможных решений, а именно, к тому, которое описано в рекомендациях. При наличии в работах учащихся других решений критерии вырабатываются предметной комиссией с учетом описанного общего подхода. Решения учащихся могут содержать недочеты, не отраженные в критериях, но которые, тем не менее, позволяют оценить результат выполнения задания положительно (со снятием одного балла). В подобных случаях решение о том, как квалифицировать такой недочет, принимает предметная комиссия.

Примеры оценивания ответов по каждому типу заданий

С развернутым ответом с комментариями.

Задача 21 (демонстрационный вариант 2017 г).

Сократите дробь .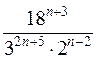

Решение.

.

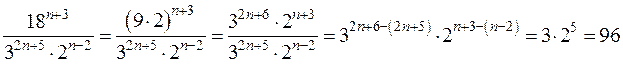Ответ: 96.

Критерии оценки выполнения задания 21.

Баллы	Критерии оценки выполнения задания
	Правильно выполнены преобразования, получен верный ответ
	Решение доведено до конца, но допущена ошибка вычислительного характера или описка, с её учётом дальнейшие шаги выполнены верно
	Другие случаи, не соответствующие указанным критериям
	Максимальный балл

Небольшое уточнение с «ошибка или описка» до «ошибки или описки» подчеркивает тот факт, что 1 балл допускается ставить в тех случаях, когда единственная вычислительная ошибка (описка) стала причиной того, что неверен ответ.

К вычислительным ошибкам не относятся ошибки в формулах при решении квадратного уравнения, действиях с числами с разными знаками, упрощении выражений со степенями и корнями и т.д.

Пример.

Решите уравнение .

Ответ: , .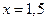

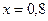Комментарий.

Работа интересная – записан верный ответ. Но присутствуют в последних строках:

а) ошибка в вычислении корня квадратного уравнения;

б) ошибка при сложении чисел с разными знаками;

в) ошибка в формуле корней квадратного уравнения;

г) ошибка при делении чисел с разными знаками.

Оценка эксперта: 0 баллов.

Задача 22 (демонстрационный вариант 2017 г).

Рыболов в 5 часов утра на моторной лодке отправился от пристани против течения реки, через некоторое время бросил якорь. 2 часа ловил рыбу и вернулся обратно в 10 часов утра того же дня. На какое расстояние от пристани он отплыл, если скорость реки равна 2 км/ч, а собственная скорость лодки 6 км/ч?

Решение.

Пусть искомое расстояние равно х км. Скорость лодки при движении против течения равна 4 км/ч, при движении по течению равна 8 км/ч. Время, за которое лодка доплывёт от места отправления до места назначения и обратно, равно 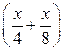часа. Из условия задачи следует, что это время равно 3 часам. Составим уравнение: 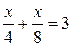. Решив уравнение, получим .

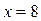Ответ: 8 км.

Критерии оценки выполнения задания 22.

Баллы	Критерии оценки выполнения задания
	Правильно составлено уравнение, получен верный ответ
	Правильно составлено уравнение, но при его решении допущена вычислительная ошибка, с её учётом решение доведено до ответа
	Другие случаи, не соответствующие указанным критериям
	Максимальный балл

Задание 22 тематически сохраняется несколько лет. Критерии его оценивания сохранились. Следует отметить, что при решении дробно-рационального уравнения, полученного в задаче, необязательно требовать от выпускника проверки условия не равенства нулю знаменателя.

Пример оценивания решения задания 22.

Игорь и Паша могут покрасить забор за 14 часов, Паша и Володя – за 15 часов, а Володя и Игорь за 30 часов. За какое время покрасят забор мальчики, работая втроем. Ответ дайте в минутах.

Ответ: 700 минут.

Комментарий.

Путь решения верный, но не учтена “удвоенная производительность”, – явно допущена вычислительная ошибка.

Оценка эксперта: 1 балл.

Задача 23 (демонстрационный вариант 2017 г).

Постройте график функции 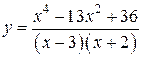и определите, при каких значениях 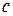прямая 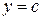имеет с графиком ровно одну общую точку.

Решение. Разложим числитель дроби на множители:

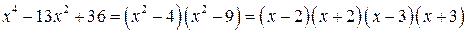
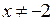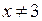При и функция принимает вид: ,

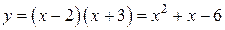её график — парабола, из которой выколоты точк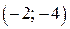и и .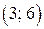

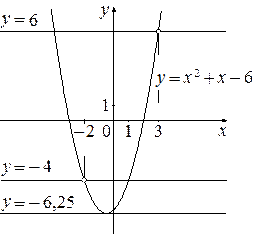
Прямая 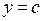имеет с графиком ровно одну общую точку либо тогда, когда проходит через вершину параболы, либо тогда, когда пересекает параболу в двух точках, одна из которых — выколотая. Вершина параболы имеет координаты .

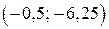Поэтому 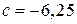, 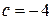или .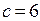

Критерии оценки выполнения задания 23.

Баллы	Критерии оценки выполнения задания
	График построен правильно, верно указаны все значения c , при которых прямая y = c имеет с графиком только одну общую точку
	График построен правильно, указаны не все верные значения c
	Другие случаи, не соответствующие указанным критериям
	Максимальный балл

Основным условием положительной оценки за решение задания является верное построение графика. Верное построение графика включает в себя: масштаб, содержательная таблица значений или объяснение построения, выколотая точка обозначена в соответствии с ее координатами.

Пример оценивания решения задания 23.

Постройте график функции и определите, при каких значениях k прямая имеет с графиком ровно одну общую точку.

Ответ: 81.

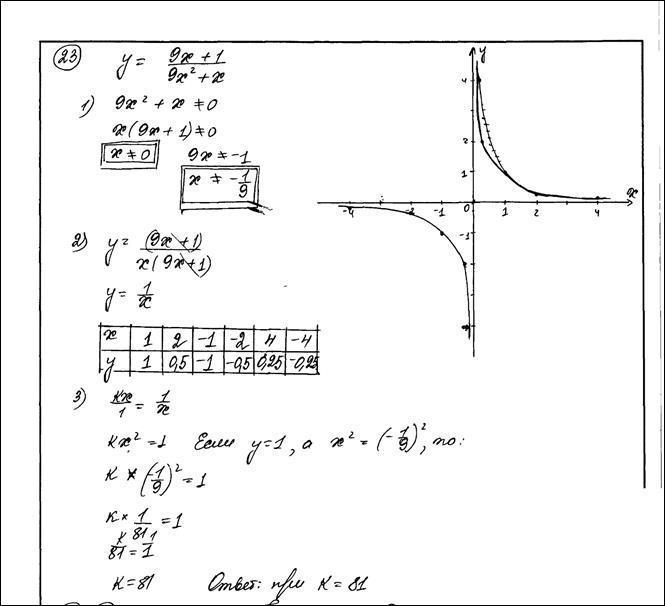
Комментарий.

График построен неверно – отсутствует выколотая точка. В соответствии с критериями – 0 баллов.

Оценка эксперта: 0 баллов.

Задача 24 (демонстрационный вариант 2017 г).

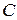В прямоугольном треугольнике с прямым углом известны катеты: 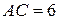, 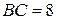. Найдите медиану 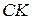этого треугольника.

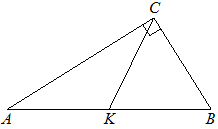Решение.

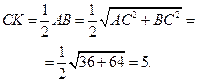
Ответ: 5.

Критерии оценки выполнения задания 24.

Баллы	Критерии оценки выполнения задания
	Получен верный обоснованный ответ
	При верных рассуждениях допущена вычислительная ошибка, возможно приведшая к неверному ответу
	Другие случаи, не соответствующие указанным критериям
	Максимальный балл

Задание 24 практически не менялось в течение нескольких лет. Критерии его оценивания сохранились.

Пример оценивания решения задания 24.

Высота, опущенная из вершины ромба, делит противоположную сторону на отрезки равные 24 и 2, считая от вершины острого угла. Вычислите длину высоты ромба.

Ответ: 10.

Комментарий.

Учащийся использует данные, которых нет в условии (считая острый угол ромба 60°).

Оценка эксперта: 0баллов.
Задача 25 (демонстрационный вариант 2017 г).

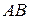В параллелограмме точка — середина стороны . Известно, что 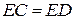. Докажите, что данный параллелограмм — прямоугольник.

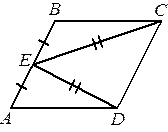Доказательство. Треугольник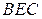и и 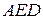равны по трём сторонам.

Значит, углы 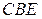и 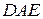равны. Так как их сумма равна 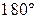, то углы равны 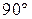. Такой параллелограмм — прямоугольник.

Критерии оценки выполнения задания 25.

Баллы	Критерии оценки выполнения задания
	Доказательство верное, все шаги обоснованы
	Доказательство в целом верное, но содержит неточности
	Другие случаи, не соответствующие указанным критериям
	Максимальный балл

Пример оценивания решения задания 25.

Пример.

Две окружности с центрами E и F пересекаются в точках C и D, центры E и F лежат по одну сторону относительно прямой CD. Докажите, что прямая CD перпендикулярна прямой EF.

Комментарий.

Не доказано, что точка F лежит на высоте EK.

Оценка эксперта: 0баллов.

Задача 26 (демонстрационный вариант 2017 г).

Основание 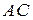равнобедренного треугольника 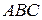равно 12. Окружность радиуса 8 с центром вне этого треугольника касается продолжений боковых сторон треугольника и касается основания 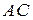. Найдите радиус окружности, вписанной в треугольник .

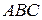Решение.

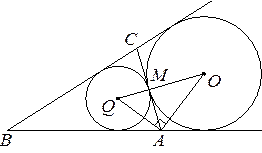Пусть 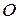— центр данной окружности,
а 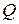— центр окружности, вписанной в треугольник .

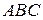Точка касания 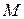окружностей делит 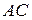пополам.

Луч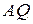и и 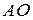— биссектрисы смежных углов, значит, угол 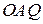прямой. Из прямоугольного треугольника 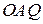получаем: 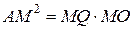. Следовательно,

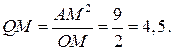
Ответ: 4,5.

Критерии оценки выполнения задания 26.

Баллы	Критерии оценки выполнения задания
	Ход решения верный, все его шаги выполнены правильно, получен верный ответ
	Ход решения верный, чертёж соответствует условию задачи, но пропущены существенные объяснения или допущена вычислительная ошибка
	Другие случаи, не соответствующие указанным критериям
	Максимальный балл

Пример оценивания решения задания 26.

Пример.

Биссектриса угла A, треугольника ABC делит высоту BH в отношении 5:4, считая от вершины. BC равно 6. Найдите радиус описанной окружности.

Ответ: 5.

Комментарий.

При правильном ответе решение содержит более одной ошибки и описки.

Оценка эксперта: 0баллов.