Типовая структура микропроцессорной системы

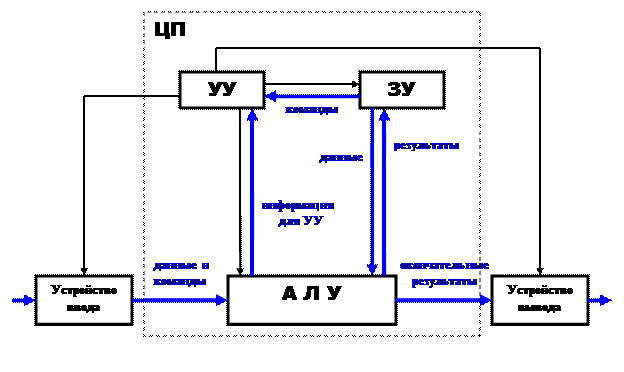
сигналы управления и адресации

информационные сигналы

Системы счисления

Двенадцатеричная система:

система мер – 1 фут = 12 дюймов

денежная система – 1 шиллинг = 12 пенсов

Шестидесятеричная система:

система измерения времени – 1 час = 60 минут

система измерения углов – 1 град. = 60 мин.

Позиционные системы счисления

Десятичная система: 5 1 1

500 10 1

"вес" цифры

Римская система: V I I

5 1 1

N_b=…d₃d₂d₁d₀ d_-1d_-2d_-3…

пример:

132.54₁₀=1∙10²+3∙10¹+2∙10⁰+5∙10^-1+4∙10^-2

Число 10 – основание системы счисления

N_b=d_q-1∙b^q-1+d_q-2∙b^q-2+…+d₁∙b¹+d₀∙b⁰+d_-1∙b^-1+…+d_-p∙b^-p=

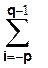= d_i∙bⁱ ,

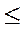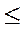где: b > 1 , 0 d_i b - 1

3. Преобразование чисел из одной системы счисления в другую

3.1. Преобразование чисел в десятичную систему счисления

A = 10, B = 11, C = 12 …

примеры:

1110.1₂ =

= 1∙ 2³ + 1∙ 2² + 1∙ 2¹ + 0∙ 2⁰ + 1∙ 2^-1 =

= 8 + 4 + 2 + 0 + 0.5 = 14.5₁₀

13F.4₁₆ =

= 1∙16² + 3∙16¹ + 15∙16⁰ + 4∙16^-1 =

= 256 + 48 + 15 + 0.25 = 319.25₁₀

3.2. Преобразование десятичных чисел в другие системы счисления

3.2.1. Преобразование целой части десятичного числа

N_b1=d_q-1∙b₂^q-1+d_q-2∙b₂^q-2+…+d₁∙b₂¹+d₀∙b₂⁰

N_b1/b₂ = N_b1¹ + d₀/b₂ =

целое частное è = d_q-1∙b₂^q-2+d_q-2∙b₂^q-3+…+d₁∙b₂⁰+

остаток è +d₀∙b₂^-1

N_b1¹/b₂ = N_b1² +d₁/b₂ =

целое частное è = d_q-1∙b₂^q-3+d_q-2∙b₂^q-4+…+d₂∙b₂⁰+

остаток è +d₁∙b₂^-1

пример 1: 52₁₀ è N₂

/2 остаток:

52 0 à d₀

26 0 à d₁

13 1 à d₂

6 0 à d₃

3 1 à d₄

1 1 à d₅

ответ: N₂ = 110100₂

пример 2: 58506₁₀ è N₁₆

/16 остаток:

58506 10₁₀ = A₁₆ àd₀

3656 8₁₀ = 8₁₆ à d₁

228 4₁₀ = 4₁₆ à d₂

14 14₁₀ = E₁₆ à d₃

ответ: N₁₆ = E48A₁₆

3.2.2. Преобразование дробной части десятичного числа

N_b1=d_-1∙b₂^-1+d_-2∙b₂^-2+…+d_-p+1∙b₂^-p+1+d_-p∙b₂^-p

N_b1∙b₂ = N_b1¹ + d_-1 =

целая часть è = d_-1 +

дробная часть è + d_-2∙b₂^-1+…+d_-p+1∙b₂^-p+2+d_-p∙b₂^-p+1

N_b1¹∙b₂ = N_b1² + d_-2 =

целая часть è = d_-2 +

дробная часть è + d_-3∙b₂^-1+…+d_-p+1∙b₂^-p+3+d_-p∙b₂^-p+2

пример 1: 0.6875₁₀ è N₂

целая часть:

*2

0.6875 1.375 à d_-1 = 1

0.375 0.75 à d_-2 = 0

0.75 1.5 à d_-3 = 1

0.5 1.0 à d_-4 = 1

0.0

ответ: N₂ = 0.1011₂

пример 2: 0.8435₁₀ è N₁₆

целая часть:

*16

0.8435 13.496 à d_{- 1} = D

0.496 7.936 à d_{- 2} = 7

0.936 14.976 à d_{- 3} = E

0.976 15.616 à d_{- 4} = F

0.616 . . . процесс бесконечен!

ответ: N₁₆ = 0.D7EF…₁₆

3.3. Двоично-восьмеричные и двоично-шестнадцатеричные преобразования

N₂ = …d₅d₄d₃d₂d₁d₀d_-1d_-2d_-3…

N₁₀ = …d₅∙2⁵+d₄∙2⁴+...+d₀∙2⁰+…+d_-3∙2^-3… =

= … (d₅∙2²+d₄∙2¹+d₃∙2⁰) ∙2³ +

+ (d₂∙2²+d₁∙2¹+d₀∙2⁰) ∙2⁰ +

+ (d_-1∙2²+d_-2∙2¹+d_-3∙2⁰) ∙2^-3… =

= …d'₁∙8¹+d'₀∙8⁰+d'_-1∙8^-1… è N₈

N16

a

b

c

d

e

f

N10

N8

N2

примеры:

N₂ è N₈ 011 011 001 . 101 100 ₂ =

= 3 3 1 . 5 4 ₈

N₈ è N₂ 5 7 . 2 ₈ =

= 101 111 . 010 ₂

N₂ è N₁₆ 0010 1110 0101 . 1100 ₂ =

= 2 E 5 . C ₁₆

Двоичная арифметика

Сложение

а + b	b =
a =
		перенос ß 1

пример сложения двоичных чисел:

111 1 ← переносы

₊ 1011.101₂

1110.001₂

11001.110₂

Вычитание

а - b	b =
a =			заём à 1

пример вычитания двоичных чисел:

* * à заём

_ 110.11₂

11.01₂

11.10₂

Умножение

а * b	b =
a =

пример умножения двоичных чисел:

11.01₂

^* 1.01₂

110100

100.0001₂

Деление

пример деления двоичных чисел:

10100000₂ 11 ₂

11 110 101₂

100

11

100

11

100

11

1₂ ß остаток

Двоичные коды

Прямой код

содержание знакового разряда:

Положительное число

Отрицательное число

примеры записи чисел в 8-и разрядном прямом коде:

0010 1011₂ = + 43₁₀ 1010 1011₂ = - 43₁₀

0000 0000₂ = + 0₁₀ 1000 0000₂ = - 0₁₀

диапазон чисел в прямом коде:

- (2^n-1 – 1) 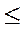X₁₀ 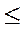+ (2^n-1 – 1),

Где n – количество разрядов двоичного числа

Обратный код

содержание знакового разряда:

Положительное число

Отрицательное число

двоичное представление отрицательного числа:

(2^n-1 – 1) - |X₁₀|

диапазон чисел в обратном коде:

- (2^n-1 – 1) 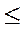X₁₀ 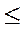+ (2^n-1 – 1),

Где n – количество разрядов двоичного числа

примеры записи десятичных чисел в 4-х разрядных двоичных кодах:

дес. числопрямойобратныйдополнительный

+7 0'111 0'111 0'111

+5 0'101 0'101 0'101

+1 0'001 0'001 0'001

+00'0000'0000'000

- 0 1'000 1'111 0'000

- 1 1'001 1'110 1'111

- 5 1'101 1'010 1'011

- 7 1'111 1'000 1'001

Дополнительный код

содержание знакового разряда:

Положительное число

Отрицательное число

двоичное представление отрицательного числа:

(2^n-1) - |X₁₀|

диапазон чисел в дополнительном коде:

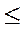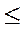- (2^n-1) X₁₀ + (2^n-1 – 1),

Где n – количество разрядов двоичного числа

Сложение и вычитание чисел со знаками

Сложение чисел в дополнительном коде

примеры сложения 5-и разрядных чисел:

+ 6₁₀ 0'0110₂ - 3₁₀ 1'1101₂

-13₁₀ 1'0011₂ -11₁₀ 1'0101₂

- 7₁₀ 1'1001₂ -14₁₀ 11'0010₂

Перенос игнорируется

пример вычитания 5-и разрядных чисел:

уменьшаемое +12₁₀ 0'1100₂ 0'1100₂

вычитаемое + 7₁₀ 0'0111₂ в доп. код 1'1001₂

разность + 5₁₀ 10'0101₂

Перенос игнорируется