Задача Коши для полубесконечной струны

Метод решения задачи Коши для бесконечной струны легко применить к случаю полубесконечной струны. Пусть струна находится в состоянии покоя на положительной оси 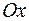и ее конец, совпадающий с началом координат, неподвижно закреплен. Тогда к уравнению колебаний струны

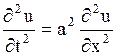(1.128)

и начальным условиям

, ,

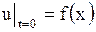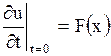(1.129)

заданным при 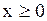, необходимо добавить еще одно граничное условие

.

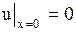(1.130)

Из условий (1.129), (1.130) следует, что .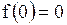

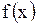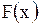Решение уравнения (1.128) при условиях (1.129), (1.130) может быть получено из формулы Даламбера (1.126) следующим образом. Допустим, что функции и , определенные сначала только для 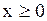, доопределены нами произвольным образом и для 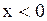. Напишем выражение :

.

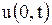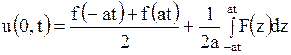(1.131)

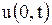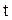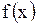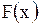Чтобы было равно нулю при всех значениях , нужно функции и при 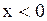определить так:

, ,

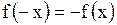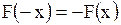т.е. функции продолжить в область отрицательных значений нечетным образом. Тогда, очевидно, первое слагаемое формулы (1.131) равно нулю; второе слагаемое также обращается в нуль, потому что берется интеграл от нечетной функции в интервале, симметричном относительно начала координат. Продолжив таким образом функци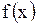и и 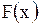на всю числовую ось, напишем формулу Даламбера:

.

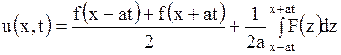(1.132)

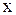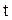Теперь это выражение определено для всех точек и и при 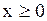дает решение поставленной задачи. Действительно, функция (1.132) удовлетворяет уравнению (1.128), условиям (1.129) и, в силу доказанного, граничному условию (1.130).

РЕШЕНИЕ УРАВНЕНИЯ КОЛЕБАНИЙ СТРУНЫ МЕТОДОМ ХАРАКТЕРИСТИК (МЕТОДОМ ДАЛАМБЕРА)

Одним из широко используемых способов решения уравнений колебаний струны является метод характеристик, называемый методом Даламбера. В основе его лежит тот факт, что с помощью замены 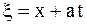, 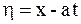уравнение

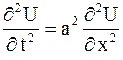(2.73)

преобразуется в уравнение 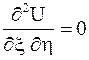, которое имеет общее решение

,

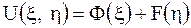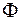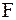где и - произвольные дважды дифференцируемые функции (см. пример 2.40). Для определения функци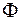й и 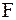, т.е. для определения закона колебаний струны, требуется использовать начальные условия, а для некоторых задач и граничные. Если вернуться к старым переменным 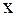и 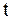, то общее решение примет вид

.

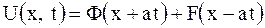Здесь 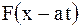характеризует прямую волну (кривая 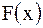смещается вправо со скоростью 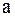), а 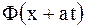- обратную волну (кривая 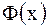смещается влево со скоростью ).

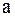Если рассматривается задача Коши для бесконечной струны 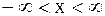, то по заданным начальным условиям

,

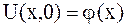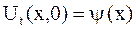(2.74)

определяются функци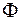и и 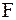, и искомое решение имеет вид

.

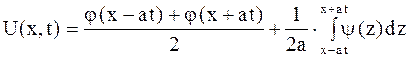(2.75)

Формула (2.75) называется формулой Даламбера. Эта формула доказывает единственность решения задачи Коши.

В частности, когда начальная скорость равна нулю ( 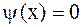), то

,

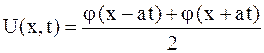откуда легко вычислить отклонение струны от положения равновесия для любой из ее точек; оно равно сумме левой и правой бегущих волн, причем начальная форма каждой волны определяется функцией 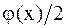, равной половине начального отклонения.

В случае полубесконечной струны, кроме начальных условий (2.74), заданных при 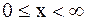, необходимо добавить еще граничное условие (конец предполагается в точке )

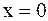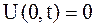(2.76)

для закрепленной в точке 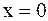струны,

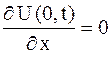(2.77)

для свободного конца в точке ,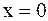

.

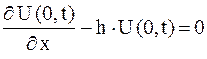для упругого закрепления в точке .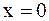

В случае однородных граничных условий (2.76) или (2.77) решение задачи о колебании полубесконечной струны сводится к решению задачи о колебании бесконечной струны путем продолжения начальных условий на всю ось нечетным образом для условия (2.76), т.е. полагают 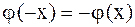, , 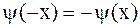и четным образом для условия (2.77), т.е. , .

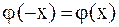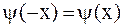Примеры решения задач

ПРИМЕР 2.43. Найти форму достаточно длинной струны, определяемой уравнением 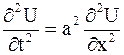, в момент времени 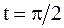, , 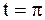если заданы начальные смещения и скорости:

а) ;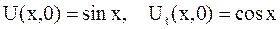

б) ;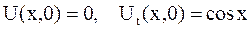

в) .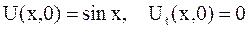

Решение. По постановке вопроса надо найти решение 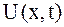задачи Коши (2.73), (2.74) в области: 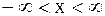, 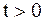. Оно определяется формулой Даламбера (2.75).

Случай а). Полагая в формуле Даламбера 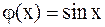, , 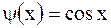найдем смещение 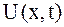в любой точке и любой момент :

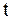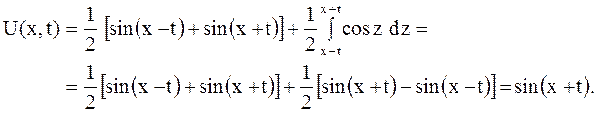
Откуда определяем форму кривой в указанные моменты времени:

, .

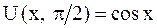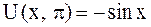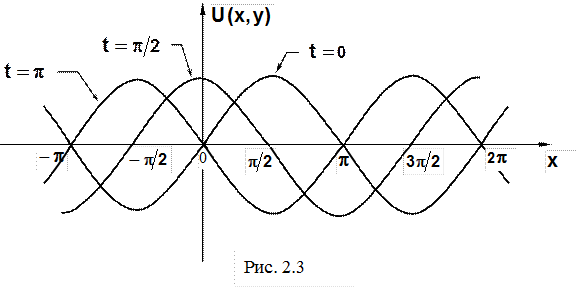
Кривые изображены на рис. 2.3.

Случай б) Начальные смещения струны равны нулю, т.к. 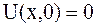. При 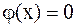колебательный процесс будет описан по формуле

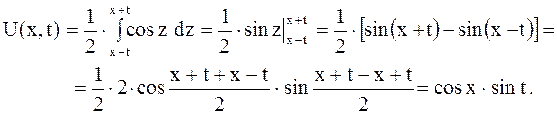
В момент времени 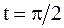струна имеет форму косинусоиды: 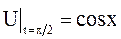, а в момент 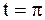она совпадает с осью абсцисс: .

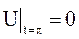Случай в). По условию, начальные скорости равны нулю, значит, 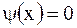. Тогда имеем

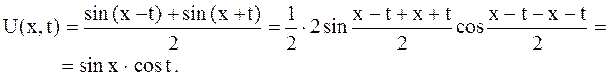
Форма струны в указанные моменты времени определяется уравнениями:

, .
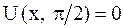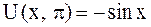