Методов моделирования. Средства моделирования

Моделирование - методы познания закономерностей развития систем, их взаимодействие с другими системами, прогнозирования и управления. Существуют следующие методы моделирования: математическое, аналоговое и физическое.

Математическое моделирование заменяет реальные объекты и их свойства математическими аналогами и устанавливает соответствие между свойствами реального объекта и характеристик его модели. Процесс познания в этом случае связан с определением физических принципов функционирования моделируемого объекта, отбора значимых факторов и информации для идентификации, анализом результатов и выработкой рекомендаций для практического использования, и стадий собственно математических, связанных с исследованием свойств модели и получением на ее основе количественных в качественных результатов. Техническими средствами для проведения математического моделирования являются компьютеры, на которых по программам выполняются расчеты. Из-за использования в расчетах компьютеров математическое моделирование относится к цифровому моделированию.

Аналоговое моделирование основано на единстве свойств процессов различной природы. Здесь реальные системы заменяют их аналогами, которые либо основаны на процессе иной физической природы по сравнению с рассматриваемыми, либо имеют ту же физическую природу. Техническими средствами электроники для проведения аналогового моделирования являются операционные усилители.

Под физическим моделированием понимается метод, основанный на исследовании модели, имеющей одинаковую физическую природу с оригиналом. Физическое моделирование заменяет эксперимент, что особенно ценно для сложных систем и машин, и даёт возможность исследовать явления, которые происходят в машине-оригинале, при сохранении их физической природы. Это не исключает, а чаще всего предполагает использование других принципов моделирования. На модельном объекте проводят измерения ряда характеристик, которые считают основными, а связи между этими характеристиками устанавливают с использованием методов математического или аналогового моделирования.

Польза от моделирования оценивается тем, насколько оно облегчает решение практических задач. Основными причинами, побуждающими вместо натурных испытаний прибегать к моделированию, являются:

1). Сложность или невозможность перевода объекта исследования в испытательный режим. Для такого перевода требуется, как правило, внесение изменений в штатную схему управления объектом.

2). Невозможность проведения исследований аварийных режимов, например, коротких замыканий, несинхронного включения генераторов на параллельную работу.

3). Дороговизна проведения экспериментов и исследований объекта. Большие затраты на контрольно-измерительную аппаратуру. Необходимость изготовления множества переносных и временных приспособлений.

4). Длительный подготовительный период перед проведением экспериментов. Необходимо также привлечения к подготовке и проведению эксперимента большого числа специалистов предприятия, на котором расположен объект исследования.

5). Ограниченность во времени возможностей проведения экспериментов и количества повторяющихся опытов. Практическая невозможность повторения экспериментов.

Рисунок В.1 - Сигнальная модель объекта наблюдения

В разработке модели и при проведении исследований на ней имеются определенные правила составления описания законов и условий функционирования проектируемого объекта, среды и способов взаимодействия объекта с нею, состава объекта, элементной базы, способов организации структуры объекта, измеряемых и настраиваемых параметров.

В общем случае, любой процесс в объекте моделирования зависит от групп параметров и сигналов, определяющих его течение и характеризующих его состояние в любой момент времени (рис.В.1).

Все сигналы образуют три группы:

1. Входные сигналы и_i (i=1,2,…т). Входными называют сигналы, значения которых могут быть измерены, но возможность воздействия на них отсутствует. Предполагается также, что значения указанных сигналов не зависят от режима процесса в объекте. Например, сигналы задания напряжение U_З и частоты f_З синхронного генератора, момента М_З и частоты ω_З вращения электродвигателя, момента сопротивления нагрузки М_С.

2. Сигналы состояния х_i (i=1,2,…n). Эти сигналы являются внутренними, относящиеся к элементам, которые входят в состав объекта и обеспечивают тем самым его правильное функционирование, например, ток i_Я двигателя, частота вращения ω, угол регулирования на выходе системы импульсно-фазового управления, величина регулируемого напряжения полупроводникового преобразователя, питающего электродвигатель.

3. Выходные сигналы у_i (i=1,2,…k). Эти сигналы доступны для наблюдения и образуются они из сигналов состояния х_i.

Если объект наблюдения является линейным звеном, то он может быть описан системой уравнений

, (В.1)

где А – квадратная матрица состояния размером ;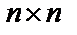

В – прямоугольная матрица управления размером .

Выходные наблюдаемые сигналы определяются через сигналы состояния матричным выражением

, (В.2)

где С– прямоугольная матрица вывода размером .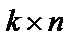

Элементы матриц А, В и С являются параметрами объекта наблюдения.

В большинстве же случаев связь X, Y, Uизвестна в алгоритмической форме, например, через числовое решение системы уравнений. Вследствие этого для нахождения вида указанной зависимости необходимо иметь определённый алгоритм решения системы уравнений математического описания, применяя который для любой совокупности значений входных и управляющих параметров, можно рассчитать величины выходных сигналов и сигналов состояния.

Математическая модель в общем случае представляет собой систему уравнений (В.1) и (В.2), отражающую сущность явлений, протекающих в объекте моделирования, которая с помощью определённого алгоритма позволяет прогнозировать поведение объекта при изменении входных и управляющих параметров. Практически любой исследуемый процесс может быть отнесён к классу объектов с сосредоточенными или распределёнными параметрами. Определяющим признаком объекта с сосредоточенными параметрами является изменение параметров, описывающих его состояние только во времени. Параметры состояния для объектов с распределёнными параметрами могут изменяться как во времени, так и в пространстве, то есть могут являться функциями пространственных координат объекта.

Содержание и форма модели определяются постановкой задачи и уровнем знаний о процессах в системе.

Математические модели, отражающие только структурные свойства объекта, например его геометрическую форму, взаимное расположение элементов в пространстве и тому подобное, называют структурным. Структурной моделью (схемой) в теории автоматического управления называют графическое изображение математической модели автоматической системы управления в виде соединений звеньев.

Математические модели, отражающие закономерности процессов функционирования объектов, называются функциональными. К их числу можно отнести систему уравнений, описывающих электрические, тепловые или механические процессы. Функциональные модели, как правило, более сложные, так как в них отражаются также сведения о структуре объектов.

Основными требованиями, предъявляемыми к математическим моделям, являются требования точности (адекватности), универсальности (массовости) и экономичности.

Адекватность. Модель считается адекватной, если отражает заданные свойства объекта с приемлемой точностью. Точность математической модели определяется степенью совпадения предсказанных или рассчитанных с ее помощью значений параметров объекта с реальными значениями. Погрешность модели зависит от значений ее параметров, которые являются элементами матриц А, В и С.

Требование универсальности математической модели предполагает возможность ее применения для описания объектов достаточно широкого класса и для анализа всех или многих режимов их функционирования.

Экономичность математической модели может оцениваться прежде всего затратами машинного времени T_МАШ, которое выражают числом элементарных операций, выполняемых при однократном решении уравнений модели. Показанием экономичности математической модели может служить также число внутренних параметров, используемых в ней. Чем больше таких параметров, тем больше затраты машинной памяти, тем больше усилий требуется для получения сведений о числовых значениях параметров и их разбросе. Требование высокой точности, большой степени универсальности, с одной стороны, и высокой экономичности - с другой, противоречивы. Чем детальнее в модели отражаются различные закономерности процессов, тем точнее и универсальнее модель, но тем больше требуемый объем вычислений и тем больше число используемых параметров, что приводит к снижению экономичности. Попытки сделать модель более экономичной обычно сопровождаются снижением точности, а иногда и универсальности. Поэтому необходим компромисс.

Вопросы для самоконтроля

1. Назовите цель моделирования и дайте характеристику основным методам моделирования.

2. Приведите обобщенную структуру моделируемого объекта и его математическое описание.

3. Назовите и дайте характеристику основным требованиям к математическим моделям.

Литература [1-9]